A fogalmak megértésének elősegítésére igyekszünk mindegyikhez példát mutatni.

Állapot

Az ágens és a környezet leírása valamilyen formában egy adott időpillanatban.

Példa: A fenti feladat egy állapota, amikor minden hittérítő és kannibál a bal parton tartózkodik, és ott van a csónak is.

Állapottér

Az állapotok halmaza az állapottér. Egy konkrét feladat megoldása során az állapottérnek csak azon része lesz érdekes, amely elérhető a megadott kezdőállapotból.

Példa: A Hittérítő- Kannibál feladat állapotterének eleme az összes olyan állapot, amelyben a hittérítők száma összesen három, a kannibálok száma összesen három, és a csónak a bal és jobb part közül pontosan az egyiken van. (A feladat megoldása során ennél valamivel kevesebb állapot lesz valóban elérhető.)

Keresési fa

Egy keresési algoritmus a működése során minden lépésben megvizsgál egy (valamilyen szisztéma szerint kiválasztott) állapotot, és az ebben az állapotban végrehajtható legális cselekvésekkel elérhető más állapotokat. Eközben felépíti az úgynevezett keresési fát, amely minden egyes újonnan felfedezett állapotot egy csúccsal, minden legális cselekvést pedig egy éllel jelöl.

Példa: Lásd például: 3. Fejezet, 3.6. ábra!

Keresési csomópont

A keresési fa csúcsait keresési csomópontoknak nevezzük.

Cél

Azon állapotok halmaza, amelyeket el szeretnénk érni a feladat megoldása során.

Példa: Minden hittérítő és kannibál a jobb parton tartózkodik, és ott van a csónak is.

Cselekvés

Az ágens lehetőségeit az állapot megváltoztatására cselekvéseknek nevezzük. A feladat megoldása tehát cselekvések egy sorozata lesz, amelyek közbülső állapotokon keresztül elvezetnek a kezdőállapotból egy célállapotba.

Példa: Egy hittérítő és egy kannibál beülnek a csónakba, és áteveznek a túlpartra.

Állapotátmenet-függvény

Cselekvések definiálására alkalmazhatók az állapotátmenet-függvények, amelyek egy adott állapothoz (cselekvés, állapot) párok egy halmazát rendelik, aszerint, hogy az adott állapotból mely cselekvések hajthatók végre, és azok mely állapotokba vezetnek.

Példa: A fenti feladatban az állapotátmenet-függvény ahhoz az állapothoz, amelyben három hittérítő és két kannibál áll a bal parton, egy kannibál pedig a jobb parton a csónakkal, azt az (cselekvés, állapot) párt rendeli hozzá, amely azt írja le, hogy az egy szem kannibál visszaül a csónakba, és visszaevez a bal partra.

Elágazási tényező

A keresési fa egy tulajdonsága, mely a fa bonyolultságának megítélésében segít. Azt mutatja meg, hogy egy adott csúcsból legfeljebb hány él vezethet ki.

Példa: A Hittérítő- Kannibál feladat esetében az elágazási tényező négy. (Ellenőrizhető a 3.9. Feladat megoldásának ábrán!)

A probléma megfogalmazásának része a cél meghatározása is, azaz meg kell adnunk egy módszert annak eldöntésére, hogy egy adott állapot célállapot-e (célteszt). Ehhez először is tisztában kell lennünk azzal, mi is a cél.

Az egyszerűség kedvéért vezessünk be rövidebb jelöléseket:

A: Állapotok halmaza

C: Cselekvések halmaza

L(s) = LEGÁLIS-CSELEKVÉS(s); L(s): A → C

E(a,s) = EREDMÉNY(a,s); E(a,s): C×A → A

A(x) = ÁLLAPOTÁTMENET-FV(x); A(x): A → C×A

Legyen A[i,j] az i-edik sor j-edik oszlopában lévő mező száma (1 ≤ i ≤ 3; 1 ≤ j ≤ 3). Az üres mezőt jelölje 0. Jelöljük az egyes lehetséges állásokat (állapotokat) az A[1,1], A[1,2],…,A[3,3] permutációval. Legyen továbbá B[k] = A[1 + ((k - 1) / n), 1 + ((k - 1) mod 3)], azaz B[1] = A[1,1], B[2] = A[1,2], … B[9] = A[3,3]. C[1,…,8] pedig legyen ugyanez, de az üres mezőt figyelmen kívül hagyva!

Definíció: egy D[1,…,n] permutáció inverzióinak száma k, ha D[a] > D[b] k darab különböző a,b párra.

Látható, hogy egy állapotban az inverziók száma meghatározható a C[1,…,8]-ból.

Most figyeljük meg a négy féle lehetséges lépést:

Mint látható, akármilyen lépést is teszünk, az inverziók száma páros számmal változik. Mivel a célállapotban az inverziók száma 0, ez azt jelenti, hogy csak olyan állapotból lehetséges a célállapotba eljutni, amelyben az inverziók száma páros!

Emlékeztetőül a "hatékony" inkrementális megfogalmazás:

Állapotok: 0 ≤ m ≤ n királynő a táblán olyan elrendezésben, hogy az n bal oldali oszlopban oszloponként pontosan egy királynő van és egyik sincs támadás alatt.

Kezdő állapot: üres tábla.

Állapotátmenet-függvény: a legbaloldaliabb üres oszlopba felhelyezünk egy királynőt úgy, hogy az ne legyen támadás alatt.

Célteszt: 8 királynő van a táblán és egyik sincs támadás alatt.

i) A képletben az n! onnan jön, hogy először n, utána n-1, aztán n-2, stb. helyre tehetjük le a királynőt legfeljebb, hiszen egy újabb sor minden lépés után kiesik! Azonban ennél kevesebb lesz a valódi lehetőségek száma, ugyanis minden újabb királynő lehelyezésével legfeljebb két további mező kiesik az átlós ütési irány miatt!

ii) A Stirling-formulát felhasználva n! ~ √(2πn)*(n/e)ⁿ, így ³√(n!) közelíthető ezzel: ⁶√((2πn)*(n/e)²ⁿ). ( (n/e)ⁿ) –t bevittük a gyökjel alá, majd az egészből harmadik gyököt vontunk. π ~ 3,14; e ~ 2,718.)

Az állapottér elemei n elemű egész típusú tömbök, azaz egy állapot tárolásához legalább n byte memóriára van szükség.

i) Véges egy állapottér, ha az állapotok száma véges. Azonban ha cselekvések egy sorozata újra és újra végrehajtható és így adott állapotokat ismételhetünk meg tetszőlegesen sokszor, akkor a keresési fa már végtelen mély lehet!

Egy nagyon egyszerű példa: adott egy ajtó, mögötte a gardrób, ahol a létrát tartjuk. A feladat a létra kivétele a gardróbból. A kezdő állapotban a gardrób ajtaja csukva, a létra pedig bent van. Ebben az állapotban legális cselekvés, hogy kinyitjuk az ajtót. Ha az ajtó nyitva van, legális cselekvés az ajtót becsukni vagy a létrát kivenni. Tegyük fel, hogy az ajtót becsukjuk. Ekkor megint legális cselekvés az ajtót kinyitni. Stb., a cselekvés-sorozat a végtelenségig folytatható, ezáltal a keresési fa pedig végtelen nagy lesz.

ii) Amennyiben az állapottér gráfja egy fa, úgy a keresési gráf szerkezetileg meg fog vele egyezni; továbbá ha az állapottér véges is, úgy a (vele szerkezetileg megegyező) keresési fa is az lesz.

iii) Általánosságban elmondható, hogy a keresési fa tulajdonképpen az állapottér gráfjának "fává egyenesített" változata. Ez a "fává egyenesítés" csak abban az esetben fogja megváltoztatni a gráf végességét, ha tartalmaz irányított kört, ekkor ugyanis lehetőség nyílik egy fent mutatotthoz hasonló 'csiki-csuki' játékra. Egyéb esetben csak véges számú véges út egymásutánjáról lehet szó, amely mindenképpen véges.

a) Négy szín felhasználásával ki kell színeznie egy síkbeli térképet úgy, hogy minden szomszédos tartomány különböző színű legyen.

Legyen a négy kiválasztott szín: kék, piros, zöld és fehér, továbbá legyen színtelen egy mező kezdetben. Egy adott állapot lehet pl. a mezők színeit tartalmazó tömb.

Kiinduló állapot: Az összes tartomány színtelen.

Célteszt: Egyik tartomány sem színtelen, és ha egy tartomány x színű, akkor egyik vele szomszédos tartomány sem x színű.

Állapotátmenet-függvény: Színezzünk be egy tetszőleges tartományt egy olyan tetszőleges színnel, amely még egyik szomszédos tartományban sem szerepel.

Útköltségfüggvény: Minden újabb színezés költsége legyen 1.

b) Egy 1m magas majom egy szobában tartózkodik, ahol van két 1m magas láda (amelyeket egymásra lehet rakni, lehet mozgatni és meg lehet mászni), és néhány banán lóg a 2,5m magas mennyezetről. A majom el szeretné érni a banánt.

Egy állapotot határozzon meg együttesen a majom és külön-külön a két láda térbeli helyzete. Az egyszerűség kedvéért legyen a szoba 1x1x1 méteres kockánként kvantált, azaz ne lehessen ennél kisebb mértékben elmozdítani a tárgyakat benne! Így a tárgyak helyének meghatározásához használhatunk egyszerű térkoordinátákat, a szoba ábrázolásához pedig egy háromdimenziós derékszögű koordinátarendszert. (A feladat jelölései: (x,y,z) -> szélesség, magasság, hosszúság.)

Kiinduló állapot: A majom és a két láda a földön helyezkednek el, egymás mellett, a banán pedig egy adott ponton lóg le a plafonról. (Pl. a majom helyzete (0,0,0), az egyik láda helyzete (0,0,1), a másik láda helyzete (0,0,-1), a banán helyzete pedig (0,2,0). A banán esetében ez azt jelenti, hogy a majomnak 2 méter magasan kell állnia, hogy már elérje.)

Célteszt: A (0,2,0) állapot az egyetlen célállapot.

Állapotátmenet-függvény: Amennyiben a majom egy láda mellett van, áthelyezheti azt egy szomszédos, üres mezőre. Ha mindkét láda mellette van, az egyik ládát ráteheti a másikra. Ha egy láda mellett van, felmászhat arra a ládára. Ha a majom egy ládán van, akkor lemászhat róla. Ha a majom egy ládába kapaszkodik, és a ládán egy másik láda is van, akkor feljebb mászhat egy ládányival.

Útköltségfüggvény: A ládák mozgatása, egy mezőnyi mozgás, a banán megszerzése és egy láda megmászása legyen mind 1 költségű.

c) Van egy olyan programja, amely "illegális input rekord" üzenetet ad, ha az input rekordok egy bizonyos állományát dolgozza fel. Ön tudja, hogy egy-egy rekord feldolgozása a többitől független. Szeretné az illegális rekordot megtalálni.

Amennyiben a feladatot magas szintű programozási nyelvek esetében tekintjük, úgy az egy egyszerű lineáris keresésnek felel meg, amely a legkevésbé sem érdekes az MI számára. Ha azonban a feladatot közvetlenül gépi szinten vizsgáljuk, úgy már más a helyzet, a keresési probléma ugyanis már nem lesz lineáris!

Egy adott állapotot határozzon meg az, hogy az olvasófej a lemez mely pozícióján áll (réteg, cilinder, stb.), cselekvés pedig legyen az olvasófej mozgatása egy másik pozícióba, amely szintén az állomány egy rekordját tárolja! A feladat továbbra sem hasonlít egy ’szokványos’ MI feladathoz, a módszerei azonban már alkalmazhatóak rá.

Kiinduló állapot: A fej a legelső pozíción van.

Célteszt: A fej egy hibás rekordot tároló pozícióban van.

Állapotátmenet-függvény: A fej mozgatható bármely olyan pozícióra, amely szintén az adott állomány egy rekordját tárolja.

Útköltségfüggvény: Egy mozgatás költsége legyen arányos a fej mozgatásához szükséges idővel!

d) Van három kancsója, egy 12 l-es, egy 8 l-es és egy 3 l-es és egy vízcsapja. A kancsókat megtöltheti, kiöntheti belőlük a vizet a földre, vagy az egyikből áttöltheti a vizet egy másikba. Pontosan 1 l vizet kell kimérnie.

A legegyszerűbb ábrázolási mód, ha a kancsók tartalmát egy háromelemű tömbben tároljuk.

Kiinduló állapot: Mindhárom kancsó üres. (A tömb tartalma (0,0,0).)

Célteszt: Valamelyik kancsóban éppen 1 l víz van. (A tömb tartalma (1,y,z) vagy (x,1,z) vagy (x,y,1).)

Állapotátmenet-függvény: Megtölthetünk egy tetszőleges kancsót, amely tartalma ekkor maximális lesz. Ha valamelyik kancsóban van víz, kiönthetjük a földre. Ekkor a kancsó üres lesz. Ha az egyik kancsóban van valami, akkor a áttölthetünk belőle annyit egy másikba, amennyi az új kancsóban még elfér. Ekkor ha az első kancsó tartalma x, a másodiké y volt, kapacitásuk pedig rendre X és Y, akkor az áttöltés után az első kancsóban x-min(x,Y-y); a másikban pedig y+min(x,Y-y) liter víz lesz. (Azaz az elsőből kitöltünk legfeljebb annyit, amennyi a másikba fér, de nyílván nem többet, mint amennyi eleve volt benne. Ezért szükséges a 'min()' függvény.)

Útköltségfüggvény: Egy megtöltés/áttöltés/kiöntés legyen 1 költségű literenként.

Megjegyzés: A feladatot tovább árnyalhatja, ha a kancsókba nem vizet, hanem valamely más folyadékot töltünk, amelynek esetében a megtöltés és a kiöntés költsége nem egyezik meg. Példa lehet erre, ha egy környezet semleges, de drága folyadékot (például bort) töltünk, amelynek kiöntése ugyan olcsó (nem káros), de a kancsó megtöltése vele drága. Vagy ha valamely veszélyes hulladéknak minősülő folyadékkal dolgozunk, akkor a kancsó megtöltése lehet lényegesen olcsóbb, mint a folyadék kiöntése a földre.

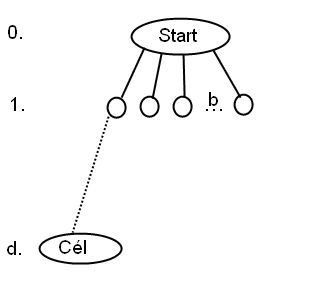
a) Rajzolja fel az állapottérnek az 1-es állapottól a 15-ös állapotig terjedő részét.

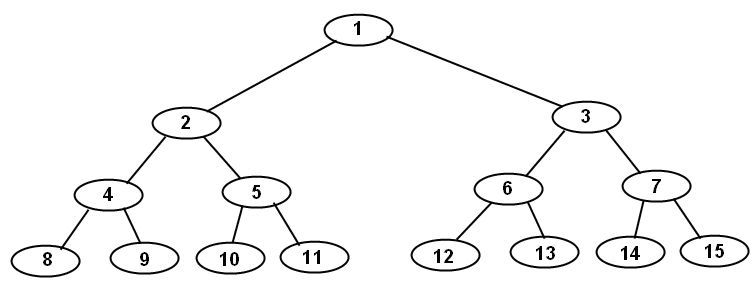
b) Tételezze fel, hogy a célállapot a 11-es. Listázza ki a csomópontok kifejtési sorrendjét szélességi, 3-as mélységkorláttal rendelkező mélységkorlátos és iteratívan mélyülő keresés esetén.

Szélességi bejárás: A gráf csúcsai sorfolytonosan vannak felcímkézve, a szélességi bejárás pedig épp ebben a sorrendben fogja kifejteni őket, így a sorrend 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11. Összesen 11 csúcsot kellett kifejteni.

3-as mélységkorlátos mélységi bejárás: Ebben az esetben az eljárás követi az utakat ameddig lehet, legfeljebb 3 mélységben, majd visszalép, ezzel gyakorlatilag mindig a fa legbaloldaliabb, még ki nem fejtett csúcsát fogja megtalálni. A sorrend 1, 2, 4, 8, 9, 5, 10, 11. Itt már csak 8 csúcsot kellett kifejteni. Látható, hogy ez a keresési módszer kevesebb csúcsot fejtett ki, mire megtalálta a megoldást, és ez általában is igaz. Ugyanakkor (rossz mélységi korlát választása esetén) nem garantált, hogy talál megoldást, és ha talál is, nem biztos, hogy az optimális lesz.

Iteratívan mélyülő keresés: Ez az eljárás lényegében megegyezik a mélységkorlátos bejárással, de azt többször végrehajtja, folyamatosan egyre növelve a mélységi korlátot a kezdeti nulláról. Amennyiben biztos ismereteink vannak a megoldás mélységéről (azaz hogy legfeljebb hány lépésre lehet a kezdőállapottól), úgy e módszer alkalmazása felesleges, de ha ilyen információnak nem vagyunk birtokában (ami a gyakorlatban bizony előfordul), akkor érdemesebb lehet ezt az iterációs módszert alkalmazni, mint választani egy túlságosan nagy korlátot, és a keresési fa egy feleslegesen terjedelmes baloldali részfáját végigjárni. (Ne feledjük: egy keresési gráf csúcsainak száma egy adott mélységben ugrásszerűen megnőhet, ahogy haladunk lefelé!) A kifejtési sorrend az első iterációban (korlát=0): 1; a második iterációban (korlát=1): 1, 2, 3; a harmadik iterációban (korlát=2): 1, 2, 4, 5, 3, 6, 7; a negyedik iterációban pedig megegyezik az előző részfeladatbeli sorrenddel (1, 2, 4, 8, 9, 5, 10, 11). Így összesen 19 csúcsot fejtettünk ki (ismétlésekkel együtt), ami nem tűnik túl kecsegtetőnek az előző megoldás 8 kifejtéséhez képest, de figyelembe véve az iménti megjegyzést belátható, hogy kevésbé egyszerű esetben sokat spórolhatunk vele!)

c) Jó lenne-e a probléma megoldására a kétirányú keresés? Ha igen, magyarázza meg részletesen, hogyan fog ez működni.

Jó módszer lenne. A kezdőállapotból elindulunk egy szélességi kereséssel, majd ezzel párhuzamosan (nem kell valódi párhuzamosság, elég felválta: innen egyet, aztán onnan egyet) elkezdünk egy mélységi keresést a végállapotból is. Amint a kifejtett állapotok halmazának metszete nem üres, a két keresés összeér és megadnak egy megoldást. A kifejtési sorrend a következő lesz:

Fentről-le: 1, 2, 3

Lentről-fel: 11, 5, 2

Elég volt tehát csak 6 csúcsot kifejteni, és máris összeértek a keresések, találtunk egy megoldást!

d) Mennyi a kétirányú keresés elágazási tényezője mindkét irányban?

Fentről lefelé (azaz a kezdőállapotból indulva) az elágazási tényező 2, ez rögtön látható a feladat megfogalmazásából. Lentről felfelé (azaz a végállapotból indulva) pedig 1, hiszen bármely állapotot csak egy korábbi állapotból lehet elérni. (Mindkettő megfigyelhető az a) ábrán.)

e) Vajon a (c) pontra adott válasz azt sugallja-e, hogy a problémának lehetséges olyan átfogalmazása, hogy az 1-es állapotból egy adott célállapothoz majdnem keresés nélkül el tudnánk jutni?

Fordítsuk meg a feladatot! Legyen a 11-es a kezdőállapot, az 1-es a célállapot, az állapotátmenet-függvény pedig a k sorszámú állapothoz rendelje a [k/2] (alsó-egészrész) sorszámú állapotot. Így, mivel minden állapothoz az állapotátmenet-függvény csak egy másik állapotot rendel, így a megoldás gyakorlatilag automatikusan adódik. (Az állapottér leegyszerűsödik egy négy elemből álló sorra (a többi állapot ugyanis nem érhető el a megadott műveletekkel), és ezen futunk végig egyenesen.)

a) Fogalmazza meg precízen a problémát. Csak azokat a megkülönböztetéseket tegye meg, amelyek a helyes megoldás érdekében szükségesek. Rajzolja fel a teljes állapottér diagramját.

Ábrázoljuk az állapotokat egy tömbbel, amelynek az első két tagja azt adja meg, hogy hány hittérítő illetve kannibál van az bal parton, a harmadik tagja pedig azt fogja tárolni, hogy hány csónak van a bal parton. (Ezzel közvetve azt is meghatároztuk, hogy mi a helyzet a jobb parton, hiszen összesen mindig három kannibál, három hittérítő és egy csónak van!)

Figyeljünk oda arra, hogy azon a parton, ahol a csónak van, lehet több kannibál, mint hittérítő (ez a 'felesleg' a csónakban ül), a másikon azonban nem! (Ezért is nagyon fontos jelölni, hogy hol van a csónak.)

Kezdőállapot: (3,3,1). Mindhárom hittérítő és mindhárom kannibál a bal parton van.

Állapotátmenet-függvény: Az állapotátmenetek a következők lehetnek:

Ugyanezek érvényesek megfordítva is, azaz a jobb partról a bal partra is.

Célteszt: (0,0,0). Mindhárom hittérítő és mindhárom kannibál a jobb parton van. (Arra nem kéne feltétlenül kikötést tennünk, hogy hol van a csónak, de egészen biztos, hogy ott a csónak, ahol az utasok is, hisz nincs aki átvigye a túlpartra, tehát ez lesz az egyetlen elérhető célállapot.)

Útköltség: Egy folyón való átkelés költsége legyen 1, az utasok számától függetlenül.

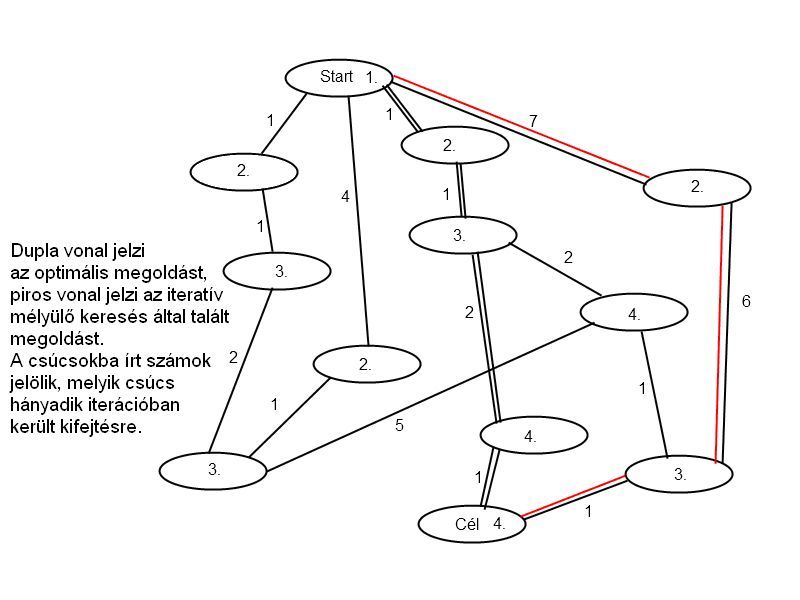
Az állapottér gráfja:

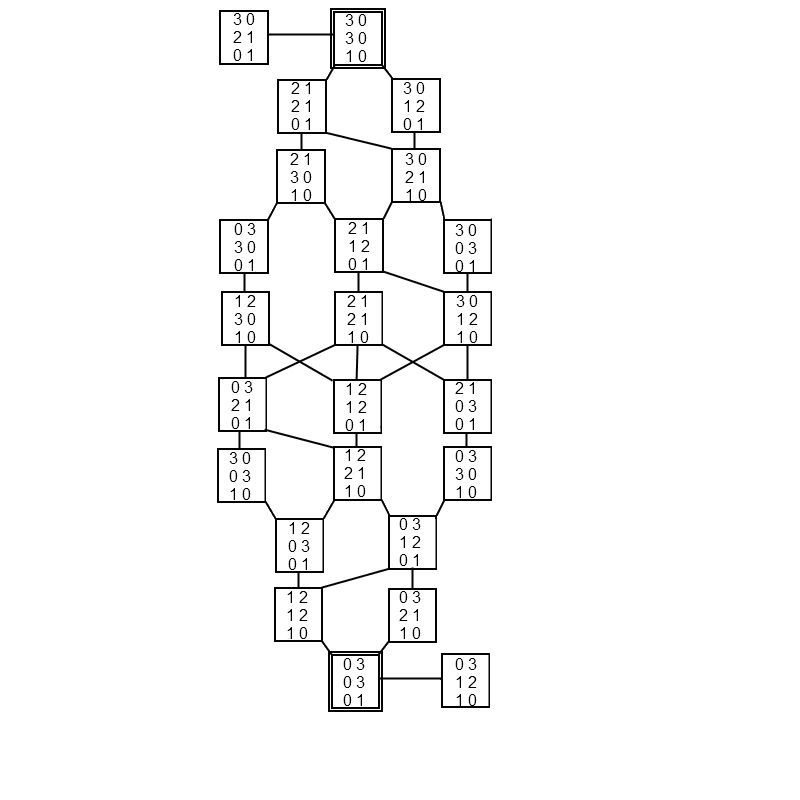
A kezdő, illetve célállapotot dupla-dobozzal jelöltük. Mivel a műveletek megfordíthatóak, minden él oda-vissza értendő. A jobb átláthatóság és érthetőség kedvéért az ábrán feltüntettük a bal és a jobb part helyzetét is: a dobozokban a baloldali oszlop mutatja a hittérítők, kannibálok és csónakok számát a bal parton, a jobboldali oszlop pedig ugyanezt a jobb parton. Még egyszer emlékeztetjük az olvasót, hogy a jobb part adatainak tárolása felesleges (redundáns) magában az implementációban, pusztán a szemléletesség kedvéért szerepelnek itt.

b) Implementálja és oldja meg optimális módon a problémát, megfelelő keresési algoritmust választva. Jó ötlet-e az ismétlődő állapotok ellenőrzése?

Figyeljük meg, hogy az állapottér gráfja szimmetrikus, hisz a két part (azaz a kezdő és a célállapot) felcserélhető! Emiatt kézenfekvőnek látszik, hogy végezzük a keresést mindkét irányból. Ebben az esetben 18 csúcs kifejtésére van szükség. Tekintve, hogy összesen 24 csúcsból áll a gráf, ez nem túl hatékony.

Mivel a megoldási csúcs a gráf ’túlsó végén van’, ezért az iteratívan mélyülő keresés is feleslegesen sokat dolgozna.

Azonban ha jobban megfigyeljük a felrajzolt gráfot, az is látható, hogy a legbaloldalibb út rögtön megoldáshoz vezet! Ezzel a tudással felvértezve jó ötletnek tűnhet mélységi bejárás használata. Így már csak 10 csúcsot kell kifejteni (ami a gráf átrendezésével tovább csökkenthető lenne).

Nagyon hasznos az ismétlődő állapotok kiküszöbölése, hisz minden cselekvés megfordítva is legális, viszont nem vezet előbbre! (A fenti két módszer vizsgálatakor mindkét alkalommal eltekintettünk a visszafelé mutató utak kifejtésétől.)

c) Véleménye szerint miért nehéz e feladvány az emberek számára, annak ellenére, hogy az állapottér ilyen egyszerű?

Figyeljük meg a különbséget az állapottér-gráf bonyolultsága és az állapotátmenet-függvény leírásának bonyolultsága között! Míg a gráf (megfelelően felrajzolva) egyszerűnek látszik (hisz abban már csak a valóban legális cselekvéseknek megfelelő élek szerepelnek), addig az állapotátmenetek kellően precíz megfogalmazása igen körülményes. Mint sok más esetben is, ha lerajzoljuk a feladatot, az nagyon sokat segíthet a megoldásában, de ha fejben próbálkozunk, nagyon gyorsan elveszítjük a fonalat!

Az első esetben értelemszerűen a memória igény lényegesen nagyobb lesz, hisz minden új csúcs generálására új memóriaterületre lesz szükség, míg ezzel szemben a második módszer esetén minden pillanatban összesen egy csúcsot kell tárolni. Azonban ha lesz szükség visszalépésre (és iteratívan mélyülő keresésnél biztosan lesz, hacsak nem megoldás az első kifejtett csúcs), úgy mivel a csúcsok közötti mozgást ennek az implementációs módszernek lépésenként kell megtennie (hisz más állapotokat nem tárol), ezért átlagos esetben lényegesen nagyobb lehet a futási ideje.

a) Mutassa meg, hogy ez az algoritmus általános útköltségek esetén optimális.

Optimális abban az értelemben, hogy optimális megoldást talál. Ez könnyen belátható: tegyük fel ugyanis, hogy nem igaz. Ebben az esetben az M megoldás, amit az algoritmus talált, nem optimális, azaz létezik egy M’ út, ami szintén megoldás, és a költsége kisebb, mint M-é. Ez azonban ellentmondás, hisz ha M’ költsége kisebb, mint M-é, akkor M’-t az algoritmusnak már egy korábbi iterációban ki kellett fejtenie az algoritmus működésének megfelelően.

b) Tekintsen egy homogén fát b elágazási tényezővel, d megoldásmélységgel és egységnyi lépésköltséggel. Hány iterációra lesz szüksége az iteratívan megnyúló keresésnek?

Kezdetben a maximális költség 0. Az első iterációban megvizsgáljuk az összes gyökérből közvetlenül elérhető b csúcsot, ezek költsége mind 1, tehát eldobjuk őket, és megjegyezzük, hogy a következő költség-korlát 1 lesz. Mivel nem találtunk megoldást, növeljük a költség-korlátot 1-re. A második iterációban megint megvizsgáljuk a gyökérből közvetlenül elérhető b csúcsot, kifejtjük őket, és azt látjuk, hogy minden újabb csúcs (b*b új csúcs) költsége 2 (1+1), tehát ezeket is eldobjuk, a költség-maximumot pedig növeljük 2-re. Ez folytatódik egészen addig, amíg a lépésköltség el nem éri d-t, ez pedig a d+1-edik iterációban lesz. Ekkor az algoritmus talál egy megoldást, és ezzel leáll.

c) Most tekintsen egy olyan lépésköltséget, amit a [0,1] folytonos tartományból sorsolnak, egy minimális pozitív epszilon költséggel. Hány iterációra lesz szükség a legrosszabb esetben?

Ebben az esetben előfordulhat, hogy az összes csúcs költsége minden esetben különböző, és a megoldás összes csúcsának költsége nagyobb, mint bármely, nem a megoldáshoz tartozó csúcs költsége. Ez a speciális eset azért különösen rossz, mert ekkor minden iterációban csak egy új csúcsot fog kifejteni az algoritmus, és egy adott szinten mindig a megoldáshoz tartozó csúcsot fejti ki utoljára. Ez azt jelenti, hogy b^d+1 iterációra lesz szükség, hogy az algoritmus megtalálja az optimális megoldást.

Fontos látni, hogy az algoritmus minden iterációban újra és újra megvizsgálja az összes korábban eldobott csúcsot is. Érezhető, hogy ez az algoritmus egészen lassú tud lenni, viszont kétségtelen előnye, hogy optimális megoldást ad. A gyakorlatban ez sokkal fontosabb lehet, mint a keresésre fordított algoritmus hatékonysága: ha a keresés 1 másodperc helyett 10 percet vesz igénybe, de egy 5 órás út helyett egy 30 perces utat talál, máris nem tűnik olyan haszontalannak a befektetés!

d) Implementálja az algoritmust és alkalmazza a 8-as játék és az utazó ügynök probléma konkrét eseteire. Hasonlítsa össze az algoritmus hatékonyságát az egyenletes költségű algoritmus hatékonyságával és értelmezze az eredményeit.

i) Ha a lépésköltség konstans, úgy a megoldás költségét a lépések száma, azaz a megoldás mélysége fogja meghatározni. Fa esetén a szélességi keresés garantálja, hogy a legrövidebb (legkevesebb lépésből álló), így legolcsóbb utat találja meg. Mivel GRÁF-KERESÉS algoritmus egy csúcshoz mindig a kezdőcsúcsból legelső utat jegyzi meg, ami a feltételek miatt optimális, így a megoldásnál is garantált, hogy az optimális lesz. Fa esetén egyenletes költségű keresésnél is garantált, hogy a megoldás optimális lesz. A fentiekhez hasonlóan, a GRÁF-KERESÉS algoritmus mindig az legelső utat jegyzi meg, ami ebben az esetben is garantáltan optimális.

ii) Ilyen probléma akkor merül fel, ha van nagyon kis mélységű, de nagy költségű út.

Már a hittérítő-kannibál feladatnál (3.9) láthattuk, hogy az iteratívan mélyülő keresés lényegesen lassabb lehet, mint az általános mélységi keresés. Könnyen mutatható olyan keresési tér, amelyben a mélységi keresés d csúcs kifejtése után talál megoldást, míg az iteratívan mélyülő keresés csak d iteráció után. Feltételezve hogy az elágazási tényező b, az iteratívan mélyülő keresésnek legrosszabb esetben 1+b+b²+b³+…+b^d-1 = O(b^d-1) csúcs kifejtésére lehet szüksége, míg a mélységi keresésnek ugyanebben az esetben lehet, hogy csak d csúcsot kell kifejtenie.

i) Javasolt inkább szélességi kereséssel próbálkozni. Vagy ha mérhető különbség van a különböző oldalak betöltési sebessége között (ez általában igaz van), akkor javasolt egyenletes költségű keresést alkalmazni. (Amihez persze előre tudni, vagy legalábbis becsülni kell a betöltési sebességeket.)

ii) A kérdésfeltevés arra utal, hogy kíséreljünk meg két irányból keresni. Ezzel a probléma nyílván a link inverzének meghatározása. Egy hiperlink nem invertálható művelet: a feladat, hogy egy weblapról eldöntsük, mely más weblapok hivatkoznak rá, maga is egy keresés, a teljes internet átkutatása az adott hivatkozás után, majd a találatok tárolása, és kifejtése. Ehhez nyílván szükséges valamiféle keresőmotor, így a hátrafelé keresés lényegesen lassabban dolgozna. Probléma továbbá, hogy az egy oldalra mutató linkek általában (kivételes esetektől eltekintve, pl. portálok, galériák) összemérhetetlenül nagyobb, mint az oldalon elhelyezett, kifelé mutató hivatkozásoké. Emiatt a visszafelé keresés feleslegesen sokat dolgozna.

iii) Mindenképp oda kell azonban figyelnünk, hogy az internet nem fa-szerkezetű, ezért mindenképp ügyelnünk kell az ismétlődő csúcsokból adódó körök levágására!

a) Tegyük fel, hogy az állapottér a sík összes (x,y) pozíciójából áll. Hány állapotról beszélünk ekkor? Hány út vezet a célig?

A sík összes pontja (de még a sír egy síkidommal határolt része is) végtelen nagyságú, ráadásul megszámlálhatatlan végtelen. Ebből adódóan a kezdő- és célállapot közötti lehetséges utak száma is végtelen. Ez nyílván kezelhetetlenül nagy az eddig ismertetett keresési algoritmusok számára. (A kulcsszó a megszámlálhatatlanság. Megszámlálható végtelen feladatot még tudnának kezelni a kereső algoritmusok, és ha van megoldás, azt meg is találnák véges időben. Azonban ha nincs megoldás, azt soha nem vennék észre, és a világ végezetéig futnának.)

b) Magyarázza el röviden, hogy egy sokszög csúcsát egy másikkal a síkban összekötő legrövidebb útnak miért kell egy olyan egyenes vonalszakaszokból állnia, amelyek az egyes sokszögek csúcsait kapcsolják össze? Adjon most egy jó állapottér definíciót. Milyen nagy ez a tér?

- Tulajdonképpen elég annyit látni, hogy a háromszög-egyenlőtlenség miatt egyenesen a csúcsokhoz kell menni az élek megkerüléséhez.

- Elegendő tehát csak a sokszögek csúcsait kell figyelembe venni mint lehetséges állapotokat. Ez az állapottér már véges.

c) Definiálja a keresési probléma implementálásához szükséges függvényeket, beleértve az állapotátmenet-függvényt, amely bemenetként egy csúcsot kap, és a belőle egyenes vonalban elérhető csúcsok halmazát adja vissza (ne felejtsük ki a szomszédos csúcsokat ugyanazon a sokszögön sem). Heurisztikus függvénynek az egyenes vonalbeli távolságot használja.

- Az állapotokat továbbra is a koordinátájukkal azonosítjuk: (x,y) eleme R×R valós számokkal, de nem engedünk meg tetszőleges állapotot, csak azokat, amelyek valamely síkidom egy csúcsát jelölik, továbbá a kezdő- és célállapotot. Az állapotok halmazát jelölje A. A cél, hogy a lehető legkevesebb mozgással az (X,Y) pontba jusson a robot. A sokszögeket jelölje S₁, S₂,...,S_n. (Egy sokszög a pontjaiból álló halmaz.)

Kezdőállapot: (x,y) = (0,0) azaz a start-pontban áll a robotunk.

Állapotátmenet-függvény: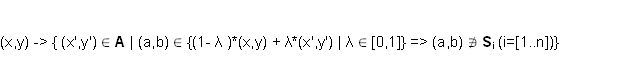

Azaz (x,y) ponthoz azon (x',y') állapottérbeli pontok halmazát rendeli, amelyekre az (x,y)-t és (x',y')-t összekötő szakasz egyik pontja sem esik bele egyik sokszögbe sem.

Célteszt: (x,y) = (X,Y) ahol X és Y a cél koordinátái.

Költségfüggvény: h( (x,y)->(x',y') ) = √(|x'-x|² + |y'-y|²) (Azaz a lépés előtti és utáni pont távolsága.)

d) Alkalmazzon a fejezetben ismertetett algoritmusok közül egyet vagy többet a tárgyterülethez tartozó problémák megoldására és értékelje azok teljesítményét.

- Ennél a feladatnál szinte garantált, hogy az útköltségek különbözőek lesznek, így a szélességi keresés nem ajánlott. Egy egyenletes költségű keresés jobb megoldást biztosít, de várhatóan lassan. Amennyiben a feladatban az akadályok a kezdő és a végpont között vannak, érdemes lehet mélységi keresést alkalmazni, ekkor ugyanis várhatóan elég gyorsan eljutunk egy megoldáshoz: a mélységi keresés gyorsan át lavírozik az akadályok között, majd a túloldalt körülnéz (az akadályok konvexitása miatt nem tud zsákutcába futni). Ha viszont a feladat ennél általánosabb, és a célállapot bárhol lehet, érdemes az egyenletes költségű keresésnél maradni. (Általában ha kevés az információ, jobb az esetleg lassú, de biztonságos egyenletes költségű keresést használni. Ha a memória kapacitás is kevés, akkor ehelyett ajánlott mélységi korlátos keresést választani.)

- Könnyen használhatunk kétirányú keresést is, mivel a feladat lényegében szimmetrikus az állapotátmenetek pedig invertálhatóak.

a) Implementálja ezt a környezetet és egy erre a környezetre vonatkozó problémamegoldó ágenst. Minden teleportálás után az ágensnek új célt kell megfogalmaznia, beleértve a saját pozíció felfedezését.

Egyelőre fennáll, hogy a robot minden esetben oda jut egy mozgási cselekvés után, ahova indult, tehát újratervezéssel és eltévedéssel egyelőre nem kell foglalkozni. A robot először megfigyeli a környezetét; ez alapján megállapítja, hol van; ezt az információt felhasználva készít egy tervet (az előző feladat szerinti módon) arra, hogy jusson el a jelenlegi helyzetéből a célállapotba, majd a megoldásként kapott cselekvéssorozatot végrehajtja. Ha a cselekvéssorozatot befejezte (a cselekvéseket tartalmazó sor üres), visszatér a környezet megfigyeléséhez, és így tovább.

c) Módosítsa a környezetet úgy, hogy az ágens az esetek 30%-ban ne a szándékolt helyen találja magát (a helyet a látható sokszögcsúcsokból sorsoljuk, ha van ilyen egyáltalán, különben nincs mozgás). Ez a valós robot hibás mozgásának egy durva modellje. Módosítsa az ágenst úgy, hogyha az ilyen hibát detektál, derítse ki, hol van, és készítsen tervet, hogy az eredeti pozícióba visszakerülhessen, ahonnan az eredeti tervét folytathatja. Emlékezzen arra, hogy néha az eredeti pozícióba visszatérés is kudarccal végződhet! Mutasson egy olyan ágenst, amely két egymás utáni hibás mozgással is sikeresen megbirkózik és eléri a célt.

Megjegyzés: Az eredeti pozíció itt azt a pozíciót jelenti, amelybe az ágens épp menni tervezett, nem a kiindulási pozíciót.

A változtatás igen egyszerű: ha a cselekvéssorozat végrehajtása során minden cselekvés végrehajtása után ellenőrizzük, hogy ott vagyunk-e, ahol a terv szerint lennünk kell. Amennyiben nem, tegyük félre a jelenlegi cselekvéssorozatot és tervezzünk egy új utat a jelenlegi pozícióból abba, ahol lennünk kellene! Jegyezzük meg továbbá azt is, hogy éppen eltévedtünk. Majd ha megvan az útvonal a kezdőállapotba, hajtsuk végre a megoldásként kapott cselekvéssorozatot. Ha ennek során újra eltévedünk, dobjuk el a jelenlegi cselekvéssorozatot és tervezzünk újat. (Ezért jegyeztük meg az imént, hogy el vagyunk tévedve.) Amennyiben sikeresen visszajutottunk abba az állapotba, amelybe az első eltévedés előtt indultunk, vegyük elő újra az eredeti tervünket (ami továbbra is egy jó terv, csak nem sikerült elsőre végrehajtani!), és próbálkozzunk meg vele újra!

d) Most két különböző visszaállítási sémával kísérletezzen egy hiba megtörténte után: (1) induljon az eredeti út legközelebb eső csúcsa felé, és (2) tervezze át az utat a cél felé az új pozícióból kiindulva. Hasonlítsa össze a három visszaállítási séma teljesítményét. Meg fogja-e változtatni az összes hasonlítás eredményét a keresési költségek figyelembevétele?

1) Továbbra is figyeljük, hogy az aktuális pozíció az-e, amire számítottunk. Ha nem, úgy tároljuk el a már megtalált megoldást, és indítsunk egy új útvonaltervezést a jelenlegi pontból az eltárolt útvonalterv legközelebbi csúcsába. Ha ez megvan, hajtsuk végre ezt a megoldást. Ha eközben megint eltévedünk, az előzőhöz hasonlóan újra próbáljuk meg megkeresni és elérni az eredeti útvonal legközelebbi pontját. Ha visszaérünk az eredeti útvonal egy pontjára, folytassuk az eredeti tervet!

2) Továbbra is figyeljük, hogy az aktuális pozíció az-e, amire számítottunk. Ha nem, felejtsük el az eredeti tervet, és a jelenlegi pozícióból készítsünk újat!

- Teljesítmény. Az első és második séma közötti különbség akkor tűnik fel, ha a legközelebbi csúcs, ahonnan folytatni szeretnénk az utat, egy akadály túloldalán van, ami azt eredményezheti, hogy az eléréséhez nagyot kell kerülni. Ez nem fordulhat elő az eredeti útiterv előző pontjával. Előfordulhat azonban olyan eset is, hogy az optimálisként megtalált út egy akadályt az egyik oldalról kerülne meg, a hiba miatt a másik oldalon indultunk el, de visszamenni az akadály elejéhez költségesebb lenne, mint azon az oldalon megkerülni, amerre már elindult az ágens. Ilyen esetben mind a második, mind a harmadik módszer jobbnak bizonyulhat.

- A keresési költség az első két módszer esetében várhatóan kisebb lesz, mint a harmadiknál, hisz ezekben az esetekben kevés lépést kell újratervezni (az elsőnél összesen legfeljebb egyet minden egymás után elkövetett hibáért), míg a harmadik esetén egy teljesen új útvonalat tervezünk, ami igen költséges lehet, ha még az út elején járt az ágens.

- Összességében leginkább az akadályok topológiáján múlik, hogy melyik újratervezési módszer a legcélravezetőbb.

e) Most tételezze fel, hogy vannak lokációk azonos "panorámával" (tételezzük fel például, hogy a világ egy négyzetrács négyzetes akadályokkal). Milyen problémákkal kell most az ágensnek szembenéznie? Milyenek most a megoldások?

- Amennyiben bármely kezdőpont "panorámája" különböző, úgy az ágens körülnézve azonnal meg tudja állapítani, hol van. Ha azonban vannak 'egyforma helyek', úgy szükséges lehet a pillanatnyi környezetnél távolabb tekinteni. Ez lényegében egy új feladat megfogalmazását jelenti: vegyük azon pontok halmazát, amelyek "panorámája" megegyezik a jelenlegivel, ez az állapothalmaz egy hiedelmi állapot lesz (125. oldal), és ebből a hiedelmi állapotból kell egy olyan tetszőleges hiedelmi állapotba eljutni, amely egyelemű (ekkor ugyanis biztosan tudni fogjuk, hol is vagyunk éppen). A kezdőpozíció ekkor egyértelműen megállapítható a megoldásból.

- Az új helymeghatározási eljárást minden olyan ponton be kell építeni az ágensbe, ahol annak ezelőtt is meg kellett keresnie a jelenlegi pozícióját a "térképen". Ez az egyszerű esetben mindössze az iteráció kezdetén szükséges, a bonyolultabb esetben (ahol a robot hibázhat) viszont minden lépés után ellenőrizni kell, hogy a megfelelő helyen van-e, ezért a megoldás összes cselekvése után végre kell hajtani. Szélsőséges esetben ez nagyon költséges lehet.

a) Tegyük fel, hogy a cselekvéseknek tetszőlegesen nagy negatív költségük lehet. Magyarázza meg, hogy ez a lehetőség miért kényszerít minden optimális algoritmust a teljes állapottér felkutatására.

Pozitív költségek esetén egy algoritmus biztosan megmondhatja egy útról, hogy rontaná a végeredményt, amennyiben annak költsége eleve nagyobb, mint az eddigi legrövidebb megoldási út költsége, így az abból a csúcsból elérhető állapotokat már nem kell figyelembe venni. Ha lehetségesek negatív élek, akkor ez már nem igaz. Előfordulhat ugyanis, hogy egy költséges él után kellően nagy negatív élek következnek, amelyek olcsóbbá teszik azt az utat. Emiatt szükségessé válik a teljes állapottér felderítése.

b) Segíteni fog-e, ha ragaszkodunk ahhoz, hogy a lépésköltség egy negatív c konstansnál nagyobb vagy azzal egyenlő legyen? Mind a fákra, mind a gráfokra gondoljon.

- Vegyünk egy olyan állapotteret, ahol minden él súlya ez a bizonyos c negatív konstans, és a gyökérből elérhető n csúcs, ebből n-1 csúcsból elérhető egy újabb csúcs, stb. Az állapottér így egy hárfához hasonlító fa lesz, és ha az ágak 'rossz' sorrendben vannak, akkor mind mélységi, mind szélességi gondolatmenettel a teljes fa bejárása szükséges, hogy a leghosszabb (és így legolcsóbb) utat megtaláljuk! A probléma tehát az, hogy még ha tudunk is egy alsó korlátot mondani az élek költségére, nem tudunk felső korlátot mondani azok számára, és emiatt az

- Gráfok esetén azonban továbbra is előfordulhat olyan eset, hogy negatív élek egy halmaza kört alkot, és ilyenkor ezen cselekvések ismételt végrehajtása tetszőlegesen lecsökkentheti egy út költségét. Erre vonatkozik a következő részfeladat.

c) Tételezzük fel, hogy a cselekvések egy halmaza ciklust alkot úgy, hogy a halmaz cselekvéseit valamilyen sorrendben végrehajtva az állapot nem változik. Milyen következményekkel jár egy ilyen környezetben tevékenykedő ágens optimális viselkedésére, ha ezen cselekvések mindegyike negatív költségű?

Pozitív él költségek esetén igaz volt, hogy egy kört végigjárni biztosan növeli az út összköltségét. Ha egy kör össz él költsége negatív, akkor ez már nem igaz: a kört tetszőleges sokszor végigjárva akármilyen kis költséget elérhetünk. Ilyenkor matematikai értelemben nem létezik optimális megoldás.

d) Könnyen el tudunk képzelni nagy negatív költségű operátorokat még az útkeresési probléma esetén is. Például néhány útszakasz olyan gyönyörű tájakon halad, hogy az idő és üzemanyag tekintetében messze túlszárnyalja a normál költségeket. Pontos megfogalmazásban magyarázza el, hogy az emberek miért nem kocsikáznak a végtelenségig a szép tájak körül, és hogyan lehetne az útkeresési problémához az állapotteret és az operátorokat definiálni, hogy a mesterséges ágens is el tudja kerülni a ciklusokat.

A kocsikázás és gyönyörű tájak példájánál a válasz egyszerű: akármilyen szép is egy táj, ha elég sokszor láttuk már, biztosan csökken az élvezeti értéke, és egy idő után a benzinköltség fontosabb szemponttá válik. Ezt úgy építhetjük be legegyszerűbben a feladat megfogalmazásába, ha bevezetünk egy idő változót, amely minden cselekvés végrehajtásával növekszik egy pozitív értékkel, és ezt felhasználjuk a h() vagy a g() függvény megfogalmazásánál! Ekkor minél tovább kocsikázunk, annál kevésbé lesz kecsegtető a körút folytatása.

e) Tud olyan valódi problémakört mondani, amelyben a lépések költsége ciklust okoz?

A legkézenfekvőbb példa a pénzkeresés, mondjuk egy pék munkája. Megvásárolja először a munkaeszközöket (egyszeri költség, azaz csak egyszer bejárt él), az alapanyagokat (ennek költsége is pozitív, hisz kiadással jár), majd munkaórákat fektet abba, hogy kenyeret süt. (Itt a költség inkább a befektetett időből adódik, de számolhatnánk akár a ráfordított energia kalóriaértékével is.) Majd ha végzett, eladja a kenyeret, aminek költsége viszont negatív lesz, hisz ezért ő kap pénzt. Ilyenkor egy intelligens ágens olyan utat választ, ahol az összköltség negatív, azaz a péknek profitja keletkezik.

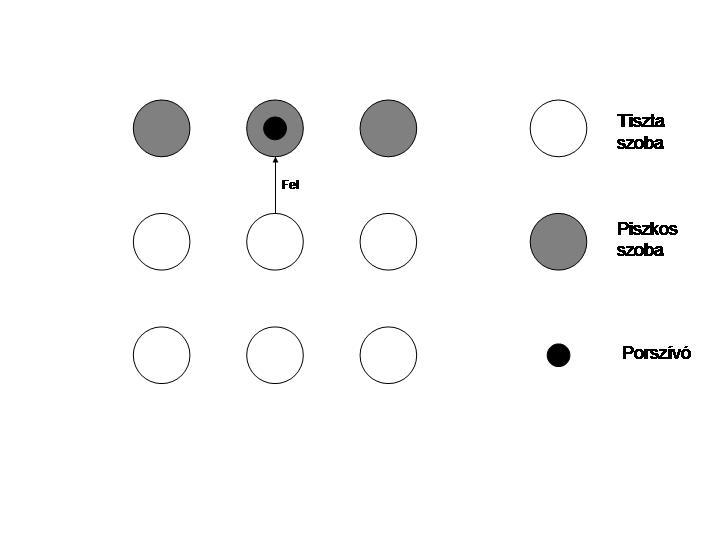
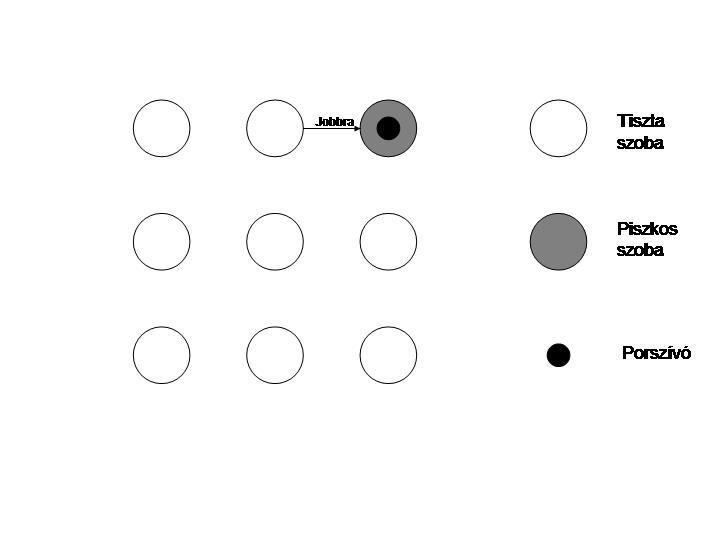
(Emlékeztetőül a Murphy-törvény azt mondta ki, hogy 'szívás' cselekvés végrehajtása után amennyiben a szobában már eleve volt kosz, úgy azt a porszívó felszívja, ha viszont nem volt, akkor koszt csinál.)

i) Az ábrán látható, hogy nincs csupa célállapotokat tartalmazó hiedelmi állapot, tehát nincs biztos megoldás. Ennek oka, hogy a szívás művelet eredményére a Murphy-szabály miatt nem tudunk következtetni a kiinduló állapot ismerete nélkül.

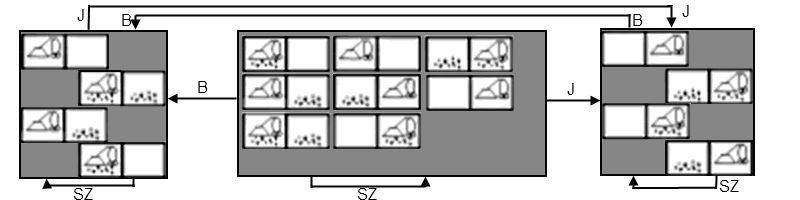
ii) Amennyiben a világ teljesen megfigyelhető, nincs semmiféle probléma. Ekkor ugyanis az ágens pontosan fogja tudni, hogy van-e kosz az adott szobában (vagy a másikban), és így nem fog 'véletlenül' koszt csinálni takarítás helyett. Így könnyen belátható, hogy a probléma megoldható legfeljebb három lépésben (ha van a szobában kosz, felszívja; átmegy a másik szobába; ha van a szobában kosz, felszívja).

a) A fejezetben ismertetett algoritmusok közül melyik lenne alkalmas e probléma megoldására? Szükséges-e, hogy az algoritmus ellenőrizze az ismételt állapotokat?

i) Mivel az állapottér tetszőleges két állapota közötti távolság csekély (legfeljebb három; ez lehet egy mélységi keresés korlátja), így bármely keresés vagy akár a véletlenszerű cselekvés-választás is hamar megoldáshoz vezet. A cselekvések költsége egységes, így legjobb a szélességi keresés az optimális megoldás megtalálása érdekében. (Ez különösen fontos lehet nagyobb állapottér esetében, ahol már nem ilyen egyértelmű, hogy mennyi is lenne egy esetleges mélységi korlát. Az iteratívan mélyülő keresés pedig igen költséges lehet!)

ii) Megint csak az állapottér mérete miatt szélességi keresés esetén előbb fogunk megoldást találni, minthogy az ismétlődő állapotok problémát okoznának. Mélységi keresésnél azonban problémát jelenthet, hogy egy adott állapotban valamely cselekvés nem változtatja meg az állapotot. Ilyenkor, ha nem ügyelünk erre, előfordulhat, hogy a mélységi keresés ezt a cselekvést próbálja ismételgetni, amíg a mélységi korlátot el nem éri (ami persze nem túl nagy). Nagyobb állapottér esetén viszont (lásd alábbi feladatok) kifejezetten fontos lesz az ismétlődő állapotok elkerülése.

(Fontos megjegyezni, hogy az állapottér elemei nem csak egy-egy szobát tartalmaznak, hanem az összeset egyszerre, a kosz eloszlásával együtt!)

b) A 3 × 3 világban alkalmazza a megválasztott algoritmust az optimális cselekvési szekvencia kiszámítására egy olyan kezdeti állapottal, ahol a felső három négyzet mindegyikében található piszok, és az ágens a középső négyzetben tartózkodik.

- Az állapotok száma egy 3x3-as porszívóvilágban 9*2^9 (a porszívó 9 helyen lehet, és mind a kilenc helyen vagy van kosz, vagy nincs). A kezdőállapotból elérhető állapotok száma viszont ennél jóval kevesebb: mindössze 9*2³=72 (ugyanis csak a felső három szobában lehet kosz).

d) Hasonlítsa össze az eddigi legjobb kereső ágens viselkedését egy olyan egyszerű, randomizált reflexszerű ágensével, amely koszt szív, ha azt megtalálja, különben véletlen módon viselkedik.

Az említett randomizált reflexszerű ágens egészen jól teljesít kisméretű porszívóvilágokban, különösen, ha a kosz valószínűsége nagy. Ha azonban a piszkos/tiszta szobák aránya csökken (akár takarítás közben, akár eleve kevés volt a kosz), úgy romlik a hatékonysága is. Már a vizsgált 3x3-as modellben is sokáig keresgélheti a sarokban maradt koszt.

e) Értékelje, hogy mi történne, ha a világot n × n -re nagyítanánk. Hogyan változna a kereső és a reflexszerű ágens teljesítménye n növelésével?

Egy tisztességes kereső algoritmussal ellátott ágens teljesítménye természetesen romlana n növelésével a keresési költség miatt (egy szélességi keresés költsége legfeljebb O(n²)). Ezzel szemben a reflexszerű ágens teljesítménye rohamosan csökken. A véletlenszerűen viselkedő porszívó nem ugyanakkora eséllyel találja meg a különböző helyeken lévő koszt: egy sarokba sokkal kisebb eséllyel "keveredik", mint egy középtájt elhelyezkedő szobába. Ahogy növeljük a tábla méretét, úgy válik egyre szembetűnőbbé a véletlenszerűség hátránya.

Készítette: Ács Gergely András, BME