1.1. Mi az MI?
A kognitív kutatások fő célja, hogy megismerjük, hogy a megismerési folyamatok, a nyelv, az érzelmek, illetve a gondolkodás hogyan alakulnak át és tárolódnak az idegrendszerben. A Mesterséges Intelligenciák gyakorlati célja pedig mindezt reprezentálni egy számítógépes rendszerben. Az MI és a kognitív kutatások szorosan együtt működnek, mivel mindkettő közös célja, hogy megismerjék az agy felépítését és azt, hogy az említett folyamatok hogyan mennek végbe az idegrendszerben. Ha megfelelően ismerjük az agy működését, csak akkor van esélyünk ezt a működést egy számítógép segítségével reprodukálni, esetleg továbbfejleszteni.
Az emberi gondolkodás legsajátságosabb elemei a humor és a viccek. A sajátosságot az adja, hogy a tanulással és egyéb kognitív folyamatokkal ellentétben ez nem figyelhető meg állatokon, így kísérletezni is csak önként jelentkezőkön lehet. A kutatások szerint ugyan az állatok is képesek nevetni,. de a nevetés oka az embereknél sem csak egy humoros helyzet lehet, sőt.[1] Robert Provine kutatásai szerint például a nevetést a beszélgetések során 80-90%-ban semmilyen humoros megjegyzés nem előzte meg, a nevetés maga sokkal inkább egy akaratlan folyamat, ami sokkal inkább egy társas jelzés, mint egy viccre való intellektuális reakció.
A humor eredeti jelentése testnedv; az ókori-középkori elképzelések szerint a különböző jellemeket a testnedvek(humores) különböző arányú keveredése határozza meg.[2] A „homour” szót az angolok a 16. század második felétől már mint hangulat, kedélyállapot használják, utána jelentése bevettől eltérő, excentrikus magatartásra módosul. A 18. századtól a humor már mint esztétikai kategória is megjelenik, főleg Jean Paul, F. W. J. von Schelling, A. W. és F. Schlegel munkáinak köszönhetően. Ekkor a humor már a romantikus képzelőerő alapeleme. Jean Paul azonosoítja is a humorost a romantikussal, illetve összekapcsolja azt a komikussal. Szerinte a humor fő forrása az egyén és a világ meghasonlása, ezt a motívumot utána S Kierkegaard viszi tovább. A 19-20. században már mint esztétikai elem jelenik meg a humor, a történelmi jelentése teljesen háttérbe szorul. S. Freud fejleszti tovább ezután a humor elméletét, szerinte a humor indulat-megtakarítás, a feszültség oldásának eszköze.
Ma főleg két terminológia létezik a humor meghatározására, az egyik az esztétikából származik, itt a humor a komikumnak csak egy részét jelenti, meg van különböztetve a szellemességtől, a gúnytól és a mókától. A humor ebben a felfogásban a különböző helyzetek feldolgozására szolgál, főleg kognitív és érzelmi eszközökkel. A másik értelmezés szerint a humor egy gyűjtőfogalom, felölelve minden olyan fogalmat, ami egy komikus vagy mókás helyzettel kapcsolatba hozható, ezzel át is véve a komikum jelentését. [3]
A kognitív humor elméletekben a legfőbb közös vonás, hogy megkívánják valamilyen eltérés, ellentmondás jelenlétét. Ez az ellentmondás vagy eltérés lehet aránytalanság; pl. „Az elefánt és a kisegér sétál a hídon, megszólal a kisegér: Hallod hogy dübörgünk?”, lehet kétértelmű fogalom, vagy hasonló hangzású szó; pl. „Amerikai óvodában rajzolni tanulnak a gyerekek:- Jack, rajzolj egy négyzetet és egy kört! –Sajnos én csak négyzetet tudok, de Tony Curtis.”, vagy egy ellentmondás a vicc elején feltételezett helyzet, és a vicc végén kirajzolódott helyzet között; pl. „Anya, hordhatok miniszoknyát? – Nem. –Anya, hordhatok tűsarkút? – Nem. –Anya, kisminkelhetem magam? – Nem. – Dehát anya, már 18 éves vagyok!! – Fejezd már be, Pistike!”
Schultz szerint a humor egyik fő forrása pont ez az eltérés az elvárt és a kapott végszó között. A humor tehát abból származik, hogy két logikailag és/vagy értelmileg különálló ötletet, helyzetet egybegyúrunk, egy váratlan vagy meglepő helyzet előállítása érdekében. Ennek az ellentétnek a fontosságát már Arisztotelész is felismerte, a humor egy szükséges elemének tekintette azt. Ez az álláspont a 18. század során sok támogatóra talált, például Gerard(1759) szerint a humor célja a szokatlan relációk keverése és a dolgok ellentétbe állítása. Beathie(1776) szerint a nevetés fő oka két össze nem illő, vagy két nem megfelelő körülmény találkozása volt. Priestley (1777) szerint pedig a nevetés a kontraszt felismerésének jelzése. Spencer(1860) azonban már azt emelte ki, hogy nem minden ellentmondás hordoz humoros tartalmat, szerinte az ellentmondás csak akkor volt vicces, ha egy nagyobb dolgot vetítettek egy kisebbre. Schoppenhauer szerint a nevetés akkor jelentkezik, amikor a hallgató hirtelen felismeri az összeférhetetlenséget a vázolt helyzet és a valós lehetőségek között. Ennek következtében az összeférhetetlenség szükséges, de nem elégséges feltételként jelentkezik az elméletekben.[3]
Egy másik elmélet szerint, ami Thomas Hobbes nevéhez fűződik, amely szerint a vicceket vagy vicces jeleneteket azért találjuk humorosnak, mert a hallgatók/nézők felsőbbrendűnek érezhetik magukat a szereplőkhöz képest. Eszerint a teória szerint a humor az ego növelésére vagy az önbecsülés javítására való eszköz, és a kellemes érzést a az önbecsülés emelkedése váltja ki. Az utóbbi évtizedek során azonban ez a teória megdőlni látszik.[4]
A viccekkel kapcsolatban az első jelentős kutatást Freud végezte, legfőbb eredményeit a 1905-ös könyvében foglalta össze. Freud a viccek osztályozása közben a következő viccet hozza példának: Egy férfi belép egy pékségbe és rendel egy tortát, de ezt hamarosan visszaviszi, és kér egy pohár italt. Ezután megissza az italt és fizetés nélkül távozik. A pék utána szól: –Nem fizette ki az italát –De adtam egy tortát cserébe –Azt sem fizette ki –Nem is ettem meg.
Freud felveti a kérdést, hogy ezt a pár mondatot hívhatjuk-e viccnek, mivel nem tudjuk, hogy pontosan milyen jellegzetességei vannak a vicceknek. Az megállapítható, hogy a humor itt is egy logikai hibából ered, de azzal pontosan nem foglalkozik, hogy a logika egésze hibás, vagy csak egy ok-okozati kapocs. Freud szerint az elménkben cenzorok működnek, és ezek tudat alatt akadályozzák meg, hogy oda nem illő dolgokra gondoljunk. A viccek azonban ki tudják játszani ezeket a cenzorokat, és ez szellemi energia felszabadulásával jár, ami jó érzést és nevetést vált ki a hallgatóból. Szerinte a viccek azért rövidek és tömörek, hogy ki tudják játszani az egyszerűen gondolkozó cenzorokat. Ezek csak a felszínes tartalmakat értik meg, a mélyebb tartalom feltárására alkalmatlanok. Freud teóriája azonban nem minden területen helytálló, a nonszensz humor esetében nem megfelelő, sokkal inkább működik a humoros agresszióra és szexualitásra. [5]
Ennek a teóriának a hibáit emeli ki, illetve javítja Marvin Minsky 1980-as esszéjében[4]. Minsky öt fő ponttal foglalkozik:
-
A józan ész nem elég megbízható a gyakorlati használatra, mert nem javítható, ezért meg kell tanulni elkerülni a leggyakoribb hibáit. A humor jó eszköz ezeknek a hibáknak a megmutatására
-
Nem elég a hibákat megtalálni, számítani kell rájuk és el kell kerülni őket. Ez a cenzorok feladata, a cenzorok nyomják el a hibás gondolatokat. Ezért foglalkozik olyan gyakran a humor „tiltott”, hibás következtetésekkel.
-
Az eredményes gondolkodáshoz ismerni kell az analógiákat és a metaforákat, azonban mindkettő hibás és félrevezető lehet, ezeknek a hibáknak a kiszűrése is a cenzorok feladata.
-
Az intellektuális hibák következményei az emberek elméjében keletkeznek, míg a szociális hibák másokat is bevonnak. A kognitív tudatalatti ezeket a hibákat ugyanolyan illetlennek találja mint a „Freudi” kívánságokat
-
A humor szociális összefüggésekben alakult ki, sokszor arra használható, hogy kíméletes módon hívjuk fel mások figyelmét a hibáikra.
Az első pont kifejtésénél Minsky a következő példát hozza: ha egy gyereknek azt mondjuk, hogy „Én most hazudok”, és elég idős ahhoz, hogy elkezdje végiggondolni az állítást, akkor nem fogja tudni eldönteni, hogy az állítás igaz, vagy hamis, és akármennyit gondolkodik rajta, nem fogja tudni, hogy mit kezdjen egy ilyen állítással. A probléma az, hogy fiatal korban még hozzá van szokva, hogy egy állításról eldönthető, hogy az igaz, vagy hamis, és a józan ész pont ezt diktálja neki. Pont az ilyen hibás előfeltevések miatt, mint ez, van probléma a józan ész használatával. Az előfeltevések eleve hibásak lehetnek, minden következtetés során lehetséges, hogy hibát követünk el, és így lehet, hogy soha nem is jutunk egy helyes következtetésre. A probléma az igazsággal van. Hogyan tudjuk valamiről eldönteni, hogy igaz? A legjobb logika eredménye is csak annyira lehet jó, mint amennyire az alapfeltevései. A matematikában ez nem probléma, mivel ott vannak egyértelmű axiómák, amiből minden mást származtatnak, de az életben ez nem ilyen egyszerű. Az életben csak nagyon kevés olyan dolog van, amire egyértelműen azt mondhatjuk, hogy igaz. A probléma akkor jelentkezik, ha kiderül valamiről, hogy nem igaz. Ha egy régi feltevésről kiderül, hogy nem igaz, akkor törölni kell minden olyan következtetést amihez ezt a feltevést felhasználtuk? Ez a kérdés a Mesterséges Intelligenciáknál is helytálló, nem mindegy, hogy ebben az esetben az összes lehetséges végkifejletet újra kell számolni, vagy csak feltételezzük, hogy azok helytállóak, és az új ismereteket csak a következő számítások során használjuk fel. Az életben az ember saját döntésén múlik, hogy ha valakit hazugságon ér, akkor abban soha többet nem bízik, és elfelejt mindent amit eddig attól az embertől hallott, vagy ezt egyedi esetnek tekinti. Ugyanez a probléma jelentkezik például nagyobb irányító logikák esetében; ha kiderül, hogy az egyik megfigyelő egység hibás eredményt szolgáltatott, akkor törölni kell minden eddigi adatot, és figyelmen kívül hagyni az összes következő jelentést, vagy egyszeri hibának kell tekinteni? Erre a kérdésre is egy megfelelően fejlett Mesterséges Intelligenciának kell megtalálnia a választ. Mindezeket a kérdéseket pedig egy olyan egyszerű vicc vetette fel, mint például az, hogy „Ez az állítás hamis”. A vicceknek tehát, azok közül is főleg a logikai következtetésekre épülőknek fontos szerepük van a megismerési folyamataink hibáinak feltárásában, és ezzel elősegítik a mesterséges rendszerekkel kapcsolatos elvárások pontosítását, az ott előfordulható hibák előrejelzését, illetve azok elhárítását.
Minsky a következő pontban a cenzorokkal foglalkozik, amik szintén fontos szerepet játszhatnak a Mesterséges Intelligenciákban. A cenzorok feladata a hibás eredményre vezető gondolatok kiszűrése, és azok tiltása. A cenzorokat Minsky két főbb csoportra osztja, az első csoport a már létrejött gondolatok tiltja le, a második csoport pedig előre megtiltja, hogy az agy bizonyos következtetésekre jusson. Az első csoport működése viszonylag egyszerű, ha egy adott gondolat megjelenik, akkor azt automatikusan tiltja. A második csoport az, aminek bonyolultabb a feladata, és pont ezek fontosak az MI szempontjából is. Az ilyen típusú cenzor előállítása azért nehézkes, mert szükség van hozzá olyan előfutárokra, amik egyértelműen jelzik az adott gondolat következtét. A cenzor készítőnek tehát ismernie kell azokat az előfutárokat, amik a nem kívánt gondolathoz vezetnek, és az előfutár gondolatnál a lehetséges következő lépések közül úgy kell választania, hogy jó következtetésre lépjünk tovább. A cenzornak természetesen tudnia kell tanulni is, és ehhez memóriára van szüksége. Szüksége van egy rövid távú memóriára, így emlékezni fog, hogy pontosan mi előzte meg az adott nem kívánt eseményt, ezen kívül pedig egy hosszú távúra, amiben tárolja az előfutárokat. Ennek a mérete egy tapasztalt cenzor esetében elég nagyra nőhet ennek következtében. Ezek alapján ha az első típusú cenzornak egy viccet mesélnénk, akkor csak a csattanó után jönne rá, hogy ezt már hallotta, de a második típusú már menet közben rájönne, hogy ismeri a viccet. A cenzoros felfogásmód magyarázza azt is, hogy miért találunk egy olyan viccet kevésbé viccesnek amit már előzőleg hallottunk. Ilyenkor vagy eleve felismerjük, hogy ismerjük a viccet, vagy egy új cenzor jön létre, vagy egy előző bővül, mivel az ismétlés egyértelművé teszi az előfutár kilétét. A Mesterséges Intelligenciák esetében ilyen cenzorok alkalmazása jelentősen megkönnyíti és meggyorsítja a helyes következtetésre jutást, mivel a cenzor felismeri, ha egy hibás eredményre vagy következtetésre jellemző előfutár jelentkezik, és a műveletet olyan irányba tereli, amivel közelebb, de legalábbis nem távolabb kerülünk a megoldástól. A cenzorok mérete főleg itt érdekes, mivel az agyban az erőforrások jóval nagyobbak, mint amit ténylegesen kihasználunk, azonban egy számítógépes rendszerben ez már nem mindig van így. A formális logikai cenzorok mérete nem kell, hogy túl nagy legyen, mivel viszonylag kevés ellentmondással paradoxszal találkozunk, de ahhoz, hogy minden nem kívánt eseményt elkerüljünk, már jóval nagyobb memóriára van szükség.[5]
Egy másik nagy kérdés a viccekkel és a humorral kapcsolatban, hogy hogyan osztályozhatjuk őket. A viccek megértéséhez humorérzék kell, de a humorérzéket magát még mindig mérni kell valahogy. Sok próbálkozás volt már olyan gépek és tesztek létrehozására, amik egyszerűen és egységesen képesek a humorérzék mérésére, de még nem született mindenki által elfogadható eredmény. Sok esetben önértékeléssel próbálkoznak, de mivel a humorérzék az emberek nagy többsége szerint egy fontos tulajdonság, ezért valószínű, hogy az emberek nagy része magasabbra értékeli a sajátját, mint amennyire az a valóságban helytálló lenne. Egy kanadai humorista szerint egy férfi nyugodtan bevallhatja, hogy nincs füle a zenéhez, vagy nincs fantáziája, esetleg hogy nem érdekli a vallás, de olyan nincs, aki azt mondaná, hogy nincs humorérzéke. A humorérzék mérő eszközök legnagyobb hibája, hogy a többségük a nevetésen keresztül méri a humorérzéket, ám a nevetés nem feltétlenül függ össze a humorérzékkel. Thorson és Powell 1993-ban kifejlesztett mérési módszere volt a legjobb eredményekkel rendelkező olyan módszer, ami már nem a nevetés mérésével dolgozik. A humort négy fő kategória szerint mérik:
-
a humor megteremtésének képessége, a kreativitás, illetve a humor felhasználásának képessége szociális célok eléréséhez
-
események feldolgozásához vagy alkalmazkodáshoz használt humor
-
a humor megbecsülése
-
a humorhoz való hozzáállás
A humorérzéken kívül a humor és viccek hatását is többen vizsgálták. Mivel ezeket kognitív folyamatoknak tekintjük, ezért jogos a kérdés, hogy milyen hatással vannak a tanulók teljesítményére, illetve az oktatásra. A humor megítélése az oktatásban azonban nem egyöntetű. Stopsky(1992) szerint a humor elengedhetetlen a kritikus gondolkozás kialakításához a diákokban. Több lehetséges módszert ad, hogy a humor milyen módon építhető be az oktatásba, azonban állításait nem tudja kísérleti eredményekkel alátámasztani. Shade(1996) szerint a humorérzék és a humor egyaránt szükségesek. Sok tanár hozza példaként a személyes tapasztalatait, miszerint a humor nagy mértékben segíti a tanulási folyamatot, azonban a kutatási tapasztalatok különböző eredményeket hoznak.
Spector (1996) fiatal diákokkal végzett tanulmánya során a következő eredményekre jutott: a gyerek kognitív képességeinek fejlődnie kell ahhoz, hogy a humorérzékük is fejlődjön. A 8 évesek körében végzett kísérletek azt mutatták, hogy már képesek megérteni az idiómákkal kapcsolatos vicceket (Kész vagy? – Teljesen..). A kísérletek megmutatták, hogy az ötödikesek már sokkal több humoros idiómát értenek, mint a harmadikosok, ezzel alátámasztva azt a teóriát, hogy a humorérzék a gyerekek fejlődésével egyenesen arányosan fejlődik. A humor használatára az oktatás során a legjobban a fiatalabb diákok reagáltak, főleg az alsóbb évfolyamokból. A gimnazistákkal és egyetemistákkal végzett kísérletek azonban már kevesebb sikert mutattak. Ebből arra következtettek, hogy a humor a fiatalok körében motiválóan hat a figyelemre, és ez magyarázná azt is, hogy az idősebb diákoknál miért nem jelentkezett a várt hatás. Az idősebbek körében a figyelemre való motiváció már inkább belső késztetésként jelentkezik, a humornak ezért nem volt jelentős hatása rajtuk. Az idősebbek körében végzett kutatásokkal azonban vannak problémák Ziv 1998-ban 11 kutatást említ a témával kapcsolatban, ezek közül 8 nem mutatott kapcsolatot a humor és az oktatás hatékonysága között, és 6 csupán meg nem jelent szakdolgozat volt. A másik nagy probléma, hogy a kutatások igen régiek, főleg 1961 és 1977 között készültek, így újakra lenne szükség. Schmidt 1994-es kutatásai szerint azonban az egyetemisták jobban emlékeznek a humoros kifejezésekre, mint az átlagosokra, így a humor és viccek szerepe nem teljesen leírható a felsőoktatásban sem.
A számítógép alapú rendszerek és a humor kapcsolatát még ennél is kevesebben kutatták, a legérdekesebb kutatást Snetsinger és Grabowski végezte 1994-ben. Egy oktatóprogramot mutattak két egyetemista csoportnak, ami kullancsokról szólt. Eredményeik szerint ugyan nem volt jelentős különbség a konkrét információ megragadása és visszaadása között a két csoportban, azonban az a csoport, amelyik a humoros anyagot kapta sokkal jobban figyelt utána a kullancsokra, illetve a kullancsok okozta fertőzésekre.
Összegzésképpen tehát a humor jó hatással van a fiatal diákok figyelmének fenntartására, azonban a tananyagtól függetlennek kell lennie, hogy ne zavarja össze a diákokat. Az idősebb diákok számára a tananyaghoz nem kapcsolódó viccek károsak lehetnek a tanulási folyamatra, azonban hosszú távon lehet, hogy jobban fognak emlékezni a tanultakra, illetve a tanulási folyamatot kellemesebbé tehetik. [4]
Oktatóprogramok illetve Mesterséges Intelligenciák készítése során érdemes figyelembe venni a fenti eredményeket. Az ember és gép kapcsolatát sokkal kényelmesebbé lehet tenni, ha a gép képes megérteni a vicceket, és esetleg képes azokra egy másik viccel reagálni.
Sokak szerint a Mesterséges Intelligencia legfőbb célja, hogy a robotokat és programokat az ember számára elfogadhatóvá tegyük, ne csak mint egy munkaeszköz, hanem mint társ is. Ennek elengedhetetlen feltétele, hogy mint minden embernek, ezeknek is legyen humorérzékük. Ez az ipar és a kutatások sok területén hasznos lenne. Elviselhetőbbé tennék a hosszú űrutazásokat az űrhajósok számára, és jobb munkamorált biztosítanának az olyan dolgozóknak, akik automata rendszerekkel és robotokkal dolgoznak nap mint nap. Egy ilyen robot létrehozása azonban ma még rendkívül komplex feladatnak tűnik. A rendszernek ismernie kéne az összes gyakori viccet, ami egy beszélgetés során előkerülhet, vallástól és kultúrától függetlenül. Ezen kívül a rendszernek képesnek kellene lennie rá, hogy felismerje, ha neki egy viccet mesélnek, és arra egy másik viccel reagálnia kéne. Ezt a viccet úgy kéne kiválasztania, hogy a legkisebb legyen a valószínűsége annak, hogy a beszélgetőpartner már hallotta a viccet, illetve el kéne tárolnia minden egyes emberhez, hogy milyen viccet mesélt nekik, illetve tőlük miket hallott a beszélgetések során. Mindez mai szemmel nézve még nagy feladatnak tűnik, de a technika rohamos fejlődése miatt valószínűleg a nem is olyan távoli jövőben mindez megvalósítható lesz. [6]
A viccek és a humor tehát több kutatás szerint is kognitív folyamatnak tekinthetők, és megértésükhöz is szükség van bizonyos kognitív fejlettségre és képességekre. Ezeknek a folyamatoknak a megértése sokat segíthet az agy felépítésének és működésének megismerésében, az agy megértése pedig fontos lépés ahhoz, hogy reprodukálni tudjuk a működését. A Mesterséges Intelligenciák létrehozásához az agy és a kognitív folyamatok megértése elengedhetetlen, az igazán hatékony programok elkészítéséhez ismerni kell, hogy az agyunk hogyan működik, illetve hogyan kerüli el azokat az általános hibákat, amikkel a mindennapi következtetések során találkozunk. Ezekre a hibákra a legtöbb példát a viccekben találjuk, ahol a humor pontosan az ilyen hibás következtetésekből származik. A viccek megértése és kutatása tehát egy fontos terület lehet, a kutatások azonban még nem elég szerteágazóak ahhoz, hogy látványos eredményekkel szolgáljanak.
[1] Jakabffy Éva, Nem viccből nevetünk
[2] Magyar Nagylexikon, IX. kötet, Magyar Nagylexikon Kiadó, Budapest, 1999
[4] Robert D. Whisonant, The Effects of Humor on Cognitive Learningin a Computer-Based Environment
[5] Marvin Minsky, JOKES and the Logic of the Cognitive Unconscious
[6]] Lance Winslow, Artificial Intelligence - Understanding a Joke and Responding with Another One
Szerző: Kerémi András, BME
Esszém témája Arisztotelész munkássága a mesterséges intelligencia vonatkozásaiban, mivel segítségével juthatott el a logika azon szintre, ahol már autonóm rendszerek külső beavatkozás nélkül, önállóan képesek logikailag bonyolult feladatok elvégzésére. Mindezt saját következtetéseik alapján, érzékelőik segítségével, képet alkotva a körülöttük lévő világról. A racionálisan viselkedő rendszereket ágensek nevezzük. Szenzorjaikkal érzékelik a környezetüket, hatással vannak rá, képesek azt meghatározott logika mentén megváltoztatni. A legnagyobb probléma viselkedésük megalkotásakor, hogy a problémamegoldást tanulniuk kell, alkalmazkodni a változó környezet okozta feltételekhez. Az intelligencia az egyén összetett, globális képessége arra, hogy célszerűen cselekedjen, racionálisan gondolkodjon, környezetében hatékonyan működjön. Ezért a viselkedését nem előre megírt feltételek határozzák meg, hanem célok, hatékonyság (reflexszerű, célorientált, hasznosságorientált ágensek közötti különbség erre világít rá). Ehhez kell a logika lehető legmagasabb szintű ismerete, hogy kellően absztrahálhassuk a cselekvések, a világ és a problémák kapcsolatát. Át tudjuk hatékonyan ültetni valamilyen programozási nyelvre, mellyel rendszerünket szeretnénk működtetni. Ezt a fejlődésfolyamatot Arisztotelész indította el, nélküle nem tarthatnánk a logikában ott, ahová eddig eljutottunk. Belőle, tudásából táplálkozott a középkori és a modern logikakutatás. Szillogisztikus következtéztetési módszere pedig mindmáig használt eszköz. Ő állapította meg, hogy kell élőket és életteleneket kategóriákba sorolni, ő próbálta meg elsőként megállapítani a szubsztanciákat, azaz az önálló léttel rendelkezőket, a dolgok lényegét, a problémák magját megtalálni. Ezáltal az ontológia úttörőjévé is vált, ami elmaradhatatlan szintén a mesterséges intelligenciához, mivel így tudja környezetét megismerni/elemezni az ágens.
Arisztotelész Kr.e. 384-ben Chalkidiké félszigetén, Stageirában született. Platón egyik legjelesebb tanítványa volt. Apja Nichomachos volt, III. Amyntas makedón király háziorvosa. Arisztotelész apjától örökölte természettudományok iránti érdeklődését, különösen érdekelte az orvostudomány és a természetfilozófia. Ezeken kívül még behatóbban foglalkozott a retorikával is. Arisztotelész volt az, aki a filozófiai rendszerelméletet és a tudományos részletkutatást egymással összeegyezteti, kiegészíti. Arisztotelész munkássága alatt kora tudományos ismereteit rendszerezte, foglalta össze. Tizenhét évesen Athénba ment, ahol Platón tanítványa lett. Kr.e. 368-348-ig tanult nála. Arisztotelész filozófiájára nagy befolyással volt a knidosi Euxodos. Platónt nagyon tisztelte, azonban kritizálta mesterét, filozófiáját. Platón halála után nem őt, hanem Speusipost választották meg az Akadémia vezetőjének. Ekkor elhagyta Athént, a troasi Assosba utazott. Itt szoros kapcsolatot alakított ki az uralkodóval, Hermisszal. Később az uralkodó unokahúgával, Pythiasszal kötött házasságot. Kr.e. 343-ban II. Philipposz király kérésére elvállalta Nagy Sándor nevelését. Nagy Sándor uralkodása alatt lehetősége volt iskolát alapítani Kr.e. 335-ben Athénban, a Lükeiont. Makedón származása miatt idegennek, kémnek tekintették az athéniak, nem övezte oly tisztelet, mint Platónt. Később ezért el is üldözték Athénból Nagy Sándor halála után. Száműzetésben halt meg Kr.e. 322-ben. Arisztotelész és Platón gondolkodása élesen elkülöníthető. Ezt jól szemlélteti Raffaello: Az athéni iskola (2. ábra) vatikáni freskója. Míg Platón az égre mutat, mint az ideák földöntúli világára, addig Arisztotelész a földi világra mutat. Arisztotelész csak is az érzékelhető tárgyakban látja a valóságot, nem elvont elmélkedést folytat, hanem kézzel fogható dolgok megismerésére törekszik. A jelenségek figyelembevétele számára módszertani szabály. [1]
Arisztotelész a tudás három fajtáját különböztette meg. A poiétikus, a praktikus és a teoretikus tudást. A poiétikus az alkotó tudás, ami a mesterségekben jelenik meg. A praktikus tudás a társadalomhoz köthető tudás: etika és politika. A teoretikus tudás elméleti tudás, mely három részre osztható: metafizika, fizika és matematika. Ezekkel a következő műveiben foglalkozik: Nikomachoszi Etika, Politika, Metafizika, Fizika, Az égbolt, Organon, Kategóriák, Első Analütika. A témával kapcsolatban most a Metafizika és Organon műveket emelném ki. Ezek különböző időben készült művek gyűjteményei, így a tanítványok és a mester munkái is megtalálhatóak közöttük. A Metafizika a tudományoknak többféle meghatározását adja meg. Egyrészt ez a dolgok alapvető okainak tudománya, a „létezővel, mint létezővel” foglalkozó tudomány. Másrészt ez a legfőbb szubsztanciának (az Első Mozgatónak, Istennek) a tudománya. [2] Arisztotelész logikával kapcsolatos műveit az Organon tartalmazza. Benne található lét és kategóriaelmélettel kapcsolatos írásai. Az organon jelentése eszköz. A logika fogalma, mely egyben kifejezi, hogy mi Arisztotelész álláspontja a logikáról: a logika minden tudomány alapja, tehát nem egy külön tudományág. Út a megértéshez a helyes gondolkodáson keresztül. Két legfontosabb írása az Organonból a Kategóriák és az Első Analütika. Utóbbiban a logikai következtetés módszeréről ír. Számos területen újat alkotott. Az arisztotelészi logika a logikai alanyra és a logikai állítmányra felbontható ítéletekkel foglalkozik.
Arisztotelésznek a mesterséges intelligenciára (MI) gyakorolt hatásának megállapításához fontos tisztázni, hogy mit is értünk MI, értelem alatt. MI-nek négyfajta irányzata terjedt el [3], amiket két dimenzió mentén értelmezhetünk: gondolkodást vagy cselekvést célozó dimenzió, illetve a célszerűség mértéke, a racionalitás dimenziója. Ezek alapján a négyféle álláspont:
-
Emberi módon gondolkodó rendszerek: kognitív, azaz a megismeréssel kapcsolatos tudományok területe, céljuk az emberi elme modellezése, megértése, működésének minél jobb közelítése.
-
Emberi módon cselekvő rendszerek: ez a megközelítés Alan Turing nevéhez kötődik, aki a gondolkodás és a cselekvés kapcsolatának vizsgálatával próbálta elkészíteni egy számítógép modelljét. Szerinte a működés, az intelligencia mércéje az emberi viselkedés minél pontosabb imitálása. Ez figyelhető meg Turing tesztjében is: egy kérdező elkülönítve egy számítógépnek és egy embernek kérdéseket tesz fel, ezeket kell megválaszolniuk. Ha a kérdező a válaszokat vizsgálva nem tudja eldönteni, melyek a gép válaszai, akkor sikeres a teszt.
-
Racionálisan gondolkodó rendszerek: nem az emberi gondolkodás követése a cél, hanem formális következtetési szabályok alkalmazásával elérni a kívánt célt.
-
Racionálisan cselekvő rendszerek: ez a jelenleg használt megközelítése az MI-nek. Célja egy adott feladat minél pontosabb végrehajtása. Nem feltétel, hogy emberek módjára gondolkodjanak, cselekedjenek az így tervezett rendszerek.
További osztályozást John. R. Searle vezetett be a gyenge és az erős MI definíciójával. Az erős MI szerint az intelligencia algoritmusok segítségével kialakítható, önálló gondolkodásra képes, az intelligencia mértéke az algoritmus bonyolultságától függ. Algoritmusok segítségével előállíthatóak az érzelmek, az értelem, a gondolkodás folyamata. A gyenge MI nem rendel agyat a rendszerhez, elegendő, ha úgy cselekszenek, mintha intelligensek lennének.
A mesterséges intelligencia kapcsán állandóan előkerül az ontológia kifejezés. Mit is jelent az ontológia? Szó szerint léttudományt jelent. Az ontológia a filozófia azon része, amely a léttel foglalkozik, annak legalapvetőbb törvényszerűségeivel. Arisztotelész mesterével ellentétben a létezőt az anyagi világban jelölte meg, nem az ideák világában. Négy létezőről beszélt, a földről, a vízről, a tűzről és a levegőről. Arisztotelész különbséget tett még a változó és az örök létezők között. Ellenállhatatlan a késztetés, hogy kijelentsük, Arisztotelész nélkül nem lenne mit leképeznünk, meghatároznunk gépeink gondolkodásához, viselkedésének szabályozásához. Alapvető fogalmainkat a logikáról ő alkotta meg. A logikában bármi fogalom, amiről állítás hozható létre. Ontológiákat az ágensek vonatkozásában a tudás és az ismeretanyagok megosztására használják a mesterséges intelligencia területén belül, elosztott tudást, információhalmazt jelölnek. Ezen információk fogalmakról készülnek. Fogalmak és viszonyok kapcsolatát vizsgálja, milyen összefüggések találhatóak közöttük. Ezek az összerendelések egy szótárban találhatóak meg. A közös szókészlet segítségével egységes fogalomkör alakulhat ki az ágensek között. Ontológia az ágensek ezen irányú kommunikációja során kialakult tartomány, modell meghatározása, relációk és objektumok definiálása. Ezek a definíciók logikai kalkulusokkal, pl. ítéletkalkulus vagy predikátumkalkulus segítségével írhatóak le attól függően, hogy ítéletlogika vagy elsőrendű logika kerül használatra. Következtetési szabályok, lépések segítségével látható be igazságtartalmuk, erre lesznek alkalmasak Arisztotelész szillogizmusai.
Ontológiák széles körben használtak tudásbázisok, elosztott rendszerek esetén. Alap ontológiának nevezzük azokat az ontológiákat, amik nem tartoznak egy konkrét probléma tartományához, doménjéhez, általános használatra készülnek. Egyetemesen elfogadott alap ontológia még nem létezik, számos megvalósítással kapcsolatos problémába ütköztek: nem magától értetődő a világ fogalmakra bontása, a „létezők” meghatározása. Az ágens működésének hatékonysága pedig attól függ, hogy az ismereteit a világról milyen mértékben képes kategorizálni. A kategorizáció a tárgyak fogalmakhoz rendelése, mely lehetővé teszi a közvetlenül nem észlelt információk következtetését. Erre épül a meghatározó tulajdonságok modellje: egy fogalom jelentését tulajdonságainak összekapcsolt listájával adhatjuk meg. Egy ilyen listában szereplő tulajdonságoktól el kell várni, hogy legyen mindegyik szükséges a fogalom meghatározásához, illetve legyenek elemiek, azaz nem bonthatóak további tulajdonságokra. Ezáltal biztosítható, hogy egyértelműen besorolható egy fogalom egy kategóriába. Arisztotelész kezdte el a kategóriák kialakítását, fogalmazta meg Metafizika című művében [4]. Szerinte a tudományoknak három dologra van szüksége:
-
Genus (nem): mely dolgok képezik a vizsgálat tárgyát
-
Principium: a bizonyítás kiinduló állításai
-
Tulajdonságok: adott genushoz tartozó dolgok tulajdonságai
Tíz kategóriát állapított meg:
-
szubsztancia (létező: ember, növény, állat, tárgy) Két alcsoport található ezen belül:
-
elsődleges: individuum (Isten, egyedi létező)
-
másodlagos: fajok, nemek (ember, állat, tárgy)
-
-
mennyiség (liternyi, négyzetméternyi)
-
minőség (fehér, kategóriákkal foglalkozó)
-
viszony (kétszerese, fele, kisebb)
-
hely (vízben, híd mellett)
-
idő (tegnap, délben)
-
helyzet (fejjel lefelé, vízszintesen)
-
birtoklás vagy ellátottság (fel van öltözve, ruhát hord)
-
cselekvés (megy, mozgat, fordul)
-
elszenvedés (tétettetik, égettetik)
Arisztotelész a logika kifejezést nem használta, nem is említi. Ő maga mindig „első filozófia”, bölcsesség néven emlegette. A művet magát Rhodosi Andronikos állította össze Arisztotelész több különböző művéből. Címének („fizika utáni”) kétféle értelmezése lehetséges: mivel vagy Arisztotelész Fizika című munkája után jelent meg, vagy pedig mélyebb okok miatt. Arisztotelész mindig azt vallotta, hogy a megismerés kétféle módon lehetséges. Egyik út a puszta fizikai érzékelés. A másik a közvetlen érzékvilágon túlra mutat: az érzékelést követően gondolkodással felfogni, megérteni egy tárgy, egy létező lényegét. Ezt megfelelő következtetések, régebbi tapasztalatok segítségével lehet elérni.
Arisztotelész követői alkották meg a peripatetikus (arisztoteliánus) logikát. Ez egy filozófiai irányzat, mely Arisztotelész tanításaira épít. Diákjai gyűjtöttek össze munkáit, dolgozták fel, vitték tovább tudását. Tagja volt többek között Theophrasztosz, a „botanika atyja”, illetve rhodoszi Andronikosz, aki rendezte, kiadta Arisztotelész műveit. Így született meg a Metafizika és az Organon is. Gyakorlati szemszögből, adott szempont szerint vizsgálnak egy témát, nem elszigetelten a valóságtól. A logika klasszikus ága ez.
Arisztotelész elsőként foglalkozott a következtetési eljárások tanulmányozásával. Eszköze a gondolkodás, jelei a szavak. Ebből kiindulva megpróbált egy szabályrendszert alkotni úgy, hogy igaz állításról bebizonyítható igazságtartalma, minden állításról eldönthető, hogy igaz vagy hamis. Így alakította ki logikai rendszerét, a szillogisztikát, ami az elmúlt évezredekben uralkodó volt a logikai következtetésekben. Immanuel Kant A tiszta ész kritikája bevezetőében írta: „A logika a legrégibb időktől kezdve ezen a biztos úton jár, ami abból látható, hogy Arisztotelész óta egyetlen lépést sem kellett hátrálnia.” Erre épül a mesterséges intelligencia kutatás logicista megközelítése, mely vallja, hogy pusztán programokra alapozva intelligens rendszerek hozhatóak létre. Már az 1960–as években készítettek olyan programokat, melyek képesek voltak a probléma logikai jellegű megfogalmazásából kiindulva a probléma megoldását megadni. Ebben az esetben informális tudást át kell alakítani, formális logikai eszközökkel ki kell fejezni. [3] Ehhez volt hatalmas segítség Arisztotelész kategóriaelmélete, következtetési eljárásai. Segítségükkel formalizálni lehetett a logikai problémákat.
Szillogizmus - formális következtetések. Az érvelés logikai modelljének alapja. Arisztotelész a szillogizmusokat három alakzat szerint felírhatónak tekintette: a következtetés, amely két előzményből (premissza) és a zárótételből (konklúzió) áll. Az egyik állítás általános érvényű tétel, ez a főtétel. A másik állítás vagy premissza egyedi, kevésbé általános, ez az altétel (vagy eset). A zárótételben található egy következtetés. A következtetés három fajtájú lehet: induktív, deduktív és abduktív. Az induktív következtetésben egy eredményből és egy esetből következtetünk a tételre, a deduktív következtetéskor egy tételből és egy esetből következtetünk az eredményre, az abduktív következtetés alkalmazásával egy eredményből és egy tételből egy esetre. A deduktív esetekben az általánosból következtetünk az egyedre, induktívkor az egyedből az általánosra. Az abdukció és az indukció feltételezésen alapuló következtetési forma. Indukciónál csak egyedi esetekre bizonyíthatjuk a tétel igazságtartalmát, nem igazolható minden esetre, mivel ha végtelen sok egyedi eset található, akkor bármely következő egyed vizsgálata cáfolhatja azt. Abdukciónál nem ismerjük az esetet, amire a tételt alkalmaztuk. Arisztotelész következtetési szabályrendszerét a későbbi időkben csak kiegészítették, a középkorban egy negyedik alakzattal egészítették ki. A középkori Margarita Philosophica enciklopédia egyik metszete (3. ábra) mutatja a középkori logikakutatás véleményét a szillogizmusokról: két vadászeb, az igazság és a hamisság üldözi a nyúl formájában található következtetési problémát. A vadász a helyes következtetési szabályok, a szillogizmusok segítségével ejti el a vadat.
Példák:
-
Abdukció
-
Tétel: A növényeknek vízre van szüksége.
-
Eredmény: Nedves a virágok földje.
-
Következtetés (eset): Meglocsolták a virágokat, esett az eső…
-
-
Dedukció
-
Tétel: Az ember halandó.
-
Eset: Arisztotelész meghalt.
-
Következtetés (eredmény): Arisztotelész ember.
-
-
Indukció:
-
Melléktétel, eset: László nem tanulta meg a leckét.
-
Eredmény: László tudatlan.
-
Következtetés (főtétel): Tanulás nélkül nincs tudás.
-
A deduktív következtetés típusai – a főtétel tulajdonságai alapján [5]:
-
Kategorikus - A főtétel egyaránt vonatkozik az egy osztályba tartozó elemekre, mivel tulajdonságaik azonosak: A gyümölcs a növény frissen fogyasztható termése, áltermése. A paradicsomnak piros termése van. A paradicsom gyümölcs.
-
Feltételes - Feltételes állításból áll a főtétel: Ha nem vesz valaki jegyet a vonatra, akkor megbüntetik. Mátyást megbüntették. Mátyás nem vett jegyet.
-
Szétválasztó - Választás található a főtételben, azonban a lehetőségek kizárják egymást: Balra kanyarodva lehet eljutni a piacra. Csak jobbra lehet fordulni.
Arisztotelésztől mindig az egyetemes igazságok megismerését kutatta, kerülte a feltételezéseket. Ezért első úttörő alakja volt a tudományoknak. Munkássága felöleli az ókori görög világ ismeretanyagát. Foglalkozott többek között filozófiával, biológiával, fizikával, matematikával, csillagászattal, pszichológiával, közgazdaságtannal, politikával, retorikával. Megfigyelései, vizsgálatai a kor korlátozott lehetőségei miatt kerültek később esetleges pontosításra, helytállóak maradtak az idők folyamán. Inspirációt adott a későbbi korok embereinek, ösztönző erőként hatott a tudományok fejlődésére.
Befejezésként, összegzésként megpróbálok Arisztotelész logikából, gondolkodásmódjából visszaadni egy keveset, hogy mit gondolt a tudományokról, a gondolkodásról - az „okosságról”, a szakmai tapasztalatokról – a „mesterségekről”. Szerinte a gondolkodás segítségével az igazságot felismerhetjük. „Minthogy a tudomány az általános és a szükségszerű dolgok megismerésére vonatkozik, s mindannak, ami bizonyításra szorul, tehát minden tudománynak, megvannak a kiinduló elvei (mert a tudomány következtetésen alapszik) … Tudományos megismerés tárgya mindig bizonyítható … Az okosság nem lehet azonos sem a tudománnyal, sem a mesterséggel. A tudománnyal azért nem, mert a cselekvés tárgya másképp is lehet, mint ahogy van. A mesterséggel pedig azért nem, mert a cselekvés és a létrehozás másnemű fogalmak. Tehát csak egy lehetőség marad: az okosság gondolkodással párosult cselekvő, igaz lelki alkat, amely arra irányul, ami az embernek jó vagy rossz. A létrehozásnak ugyanis önmagán kívül eső célja van, ellenben a cselekvésnek nem, hiszen a jó cselekvés maga a cél … Nyilvánvaló tehát, hogy az okosság valamiféle erény … Tehát az okosság az ésszel éppen ellentétes szerepet játszik; az ész ugyanis azokra a határt alkotó tételekre vonatkozik, amelyek nem okolhatók meg, az okosság viszont a végső egyedi esetre vonatkozik, amelyet nem ragadhat meg a tudomány, hanem csak az észlelés, nem az egyes érzékszervek sajátos tárgyaira vonatkozó észlelés, hanem olyanfajta észlelés, amilyennel a matematikában azt észleljük, hogy az előttünk álló egyedi alak háromszög.”[6]
[1] Kapitánffy István - Szepessy Tibor: Az ókori görög irodalom (Vázlatos áttekintés), 135-142. oldal, Budapest, 2005.
[2] Steiger Kornél: Bevezetés a filozófiába, 2. fejezet, Szöveggyűjtemény, Budapest, 2004. ISBN 963-346-263-0
[3] Csáji Balázs Csanád - A mesterséges intelligencia filozófiai problémái, Szigorlati dolgozat, Budapest, 2002., letöltés dátuma: 2010. december 8., http://www.sztaki.hu/~csaji/CsBCs_MI.pdf
[4] Birta Zsolt: Arisztotelész kategória elmélete és szubsztancia felfogása, Jegyzet kivonat, letöltés dátuma: 2010. december 8., http://szabadbolcsek.uw.hu/documentumok/filotori/okor/filtor-okor-arisztotelesz-kategoriaelmelet-es-szubsztancia-felfogas-by-bzs.doc
[5] Fazekas Project - Kulturális Enciklopédia, Szillogizmus szócikk, letöltés dátuma: 2010. december 3., http://enciklopedia.fazekas.hu/retorika/Szillogizmus.htm
[6] Arisztotelész: Nikomakhoszi etika, Hatodik könyv, letöltés dátuma: 2010. december 7., http://users.atw.hu/irodalomelmelet/nikoma.pdf
[1] Arisztotelész mellszobra, letöltés dátuma: 2010. december 6., http://sdt.sulinet.hu/data/c443b57c-e031-4e05-b2d5-93635aedf416/1/5/ResourceNormal/22_87_arisztotelesz.jpg
[2] Raffaelo: Az athéni iskola, letöltés dátuma: 2010. december 6., http://kaptarlako.freeblog.hu/files/platon_et_aristotle_rafaello_stanzasign_res.jpg
[3] Gregor Reisch, Typus logicae, Margarita Philosophica, letöltés dátuma: 2010. december 6., http://upload.wikimedia.org/wikipedia/commons/4/44/Gregor_Reisch%2C_Margarita_Philosophica%2C_Typus_Logice.jpg
Szerző: Likker Ádám, BME
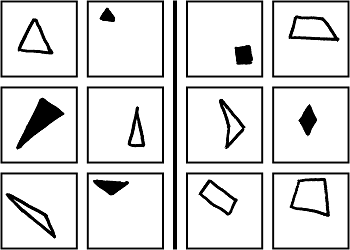
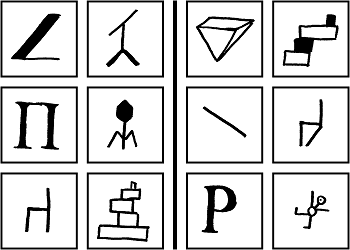
A Bongard problémák először 1967-ben, Mikhail Moiseevitch Bongard könyvében jelentek meg, amit 1970-ben Pattern Recognition címmel fordítottak angolra. Igazán ismertté csak 1979-ben váltak, Douglas R. Hofstadter: Gödel, Escher, Bach: An ethernal golden braid című munkája által. Egy probléma 12 fekete-fehér képből áll, hat a bal, és hat a jobb oldalon. A megoldás egy szabály megtalálása, ami az összes bal oldali ábrán teljesül, de egyik jobb oldalin sem. A jobb oldali ábráknak lehet saját leíró szabálya, sokszor a bal oldali szabály ellentéte, de ez nem kötelező. A továbbiakban a szakirodalmat követve, Bongard probléma helyett a BP rövidítést használom, az egy oldalon álló képeket pedig osztálynak nevezem. Az ábrákon bemutatok néhány problémát és azok megoldásait.
A Bongard problémákat alkalmazzák a pszichológia területén, alkalmassági vizsgaként, és a mesterséges intelligencia számára is komoly, összetett kihívást jelentenek. Egy olyan program, ami a megoldásukat keresi, bemenetként egy fekete-fehér pixelekből álló képet kap. Ahhoz, hogy ezt elemezni tudja, először objektumokká kell alakítania (pont, szakasz, háromszög, négyszög, stb.). Felmerül a kérdés, hogy megtehető-e ez egyetlen képet figyelembe véve, azaz létezhet-e egyértelmű hozzárendelés a képek és objektumok között. A továbbiakban az [1] forrás alapján összefoglalom, milyen nehézségekbe ütközik egy ilyen hozzárendelés.
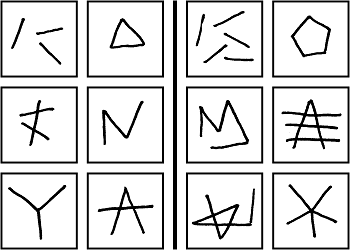
Számos olyan probléma van, ahol ugyanazt a képet alapjaiban eltérő módon kell értelmezni. Ennek egy példája, hogy egy objektumot vizsgálhatunk egészében, vagy felbonthatjuk részekre. BP 6-nál a bal fölső ábra egy háromszög, míg ugyanez a kép BP 85-ben három szakaszt jelent. Szintén BP 85-ben egy szakaszt egynek kell venni, akkor is ha más szakaszok metszik, míg BP 87-ben minden metszéspont két részre osztja az eredeti szakaszt. Még súlyosabb probléma, amikor egy képet olyan objektumnak kell tekinteni, ami valójában nincs ott. Erre példa BP 97, ahol sok pont, vonal vagy kör egy háromszöget alkot. Mindebből az következik, hogy nem lehet egy képet önmagában értelmezni, csak egy egész problémát.
Sok esetben a képeket nem lehet elemi geometriai fogalmak segítségével leírni, mint például BP 19 esetében, ahol a “nyak” fogalom a megoldás kulcsa. Ebből látható, hogy nem lehet előre megadni az összes objektumot, vagyis a programnak képesnek kell lennie tanulásra, és új fogalmak alkotására.
Bizonyos esetekben ki kell szűrni a képekből a fontos információt. Ez lehet a képfeldolgozásnál jelentkező zaj (BP 98) vagy fölösleges adatok, amik a megoldás keresését nehezítik (BP 73).
Miután meghatároztuk az objektumokat, már csak az osztályokat megkülönböztető szabályt kell megtalálni. Erre Hofstadter kidolgozott egy módszert, amit a következőkben ismertetek [2] alapján. Alkossunk egy sémát, ami egy osztály minden tagján értelmezhető, például soroljuk fel az összes előforduló objektum típust. Ezt a sémát töltsük ki adatokkal minden kép alapján, vagyis gyűjtsük össze az adott objektum típusból megjelenő példányok számát, méretét, színét, helyzetét, stb. Ezután keressünk hasonlóságokat a leírások között, amik alapján a sémákat tovább bonthatjuk alsémákra.
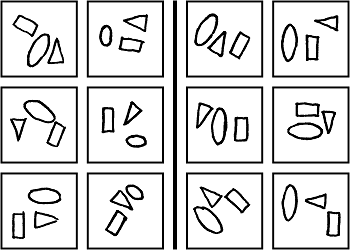
BP 49 esetén közös objektum típus a zárt görbe. A főséma:
-
zárt görbe
Objektum példányok felsorolása a bal alsó képhez:
-
zárt görbe: 1 nagy háromszög, 6 kis kör
Ha ezt minden képre megtesszük, észrevehetjük, hogy mindenhol egy nagy görbe és hat kis kör van. A felbontott séma:
-
nagy zárt görbe
-
hat kis kör
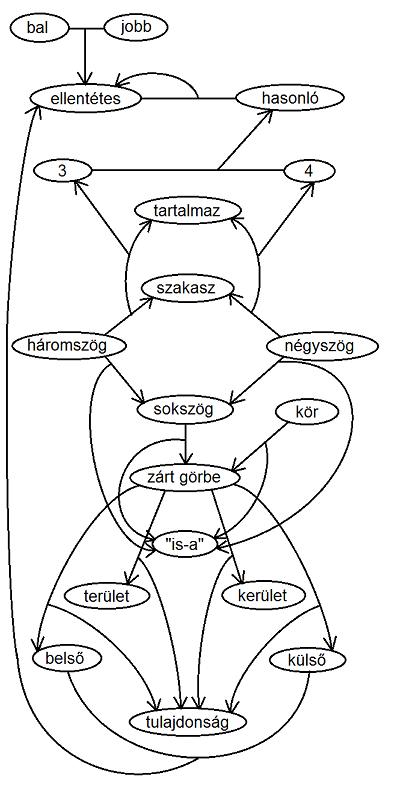
A továbblépéshez szükséges, hogy külön vizsgáljuk a zárt görbén kívül és belül eső területet. Ehhez nyújt segítséget a fogalomháló. Ez egy irányított gráf, aminek csúcsaiban geometriai alapfogalmak, képértelmezés közben alkotott új fogalmak (“nyak”) és tulajdonságok vannak. Két csúcsot akkor köt össze él, ha a két fogalom valamilyen módon összekapcsolódik, mint például a háromszög a hármas számmal vagy a területtel. Egy él és egy csúcs között is lehet él, ekkor az első él a csúcsban ábrázolt kapcsolatot jelöli az irányításnak megfelelően, például: a háromszög tartalmazza a szakaszt. Ha a sémában megjelenik egy fogalom, a gráfban hozzá kapcsolódó fogalmak is aktivizálódnak, tehát tulajdonképpen ez a módszer az agyműködést modellezi. A programozó megadhat egy alapgráfot, de nem egyértelmű, hogy a megjelenő új fogalmakat a program hogyan építse be ebbe a gráfba. Hofstadter könyvében található egy példa ilyen fogalomhálóra, amit kiegészítettem, hogy BP 49 megoldható legyen vele, így többek közt kiolvasható belőle, hogy a bal és a jobb ellentétek, az ellentétes és a hasonló ellentétek, a háromszög három szakaszból áll, a négyszög négy szakaszból, a háromszög és a négyszög sokszögek, a sokszög és a kör egy zárt görbe, a zárt görbének van belseje és külseje, amik ellentétek, illetve területe és kerülete.
Az ábrán a zárt görbe aktiválja a kívül és belül fogalmakat, ez alapján a bal alsó kép leírása:
-
zárt görbén belül: három kis kör
-
zárt görbén kívül: három kis kör
Az itt megjelenő hármas szám aktiválja a háromszöget:
-
zárt görbén belül: egyenlő szárú háromszög
-
zárt görbén kívül: egyenlő szárú háromszög
A háromszög egy sokszög, a sokszög pedig zárt görbe, amihez tartozik terület és kerület tulajdonság:
-
zárt görbén belül: egyenlő szárú, x területű háromszög
-
zárt görbén kívül: egyenlő szárú, y területű háromszög
Ha minden képre kiszámoljuk x-et és y-t, már megfogalmazhatjuk a szabályt, mi szerint a bal oldalon x<y, a jobb oldalon x>y.
A módszert Hofstadter és a Fluid Analogies Research Group továbbfejlesztette, és a későbbiekben bemutatott Phaeaco program is alkalmazza.
Előfordulhat, hogy egy leírásból nem tudjuk közvetlenül kiolvasni a megoldást, pedig valamilyen formában már benne van. Ekkor alkalmazható a meta-leírás módszer, vagyis a leírásról készült leírás, ahol magasabb absztrakciós szintről szemléljük a problémát, hátha így észreveszünk valami újat. Egy meta-leírás sémája például a következő lehet:
-
felhasznált fogalmak
-
ismétlődések a leírásban
BP 91 bal oldalán a jobb alsó képnél az objektumok felsorolása a következő:
-
görbe szakasz
-
kicsi fekete kör
-
kicsi fekete kör
-
kicsi fekete kör
Az ebből készített meta-leírás:
-
felhasznált fogalmak: görbe, szakasz, kör, kicsi, fekete
-
ismétlődések: 3 példányban “kicsi fekete kör”
Így megjelenik a hármas szám, ami végül el fog vezetni a megoldáshoz. Ebben az esetben ugyanezt talán egyszerűbben is megállapíthatta volna a program, de előfordulhat, hogy csak ez a módszer vezet el a megoldáshoz. Nagyon fontos a rugalmasság, a programnak nem szabad elakadnia, ha egyszer rossz irányba indult el.
Ebben a részben a Bongard problémák megoldására készített programok működési elvét és eredményeit vizsgálom meg [4]. Az elsőt 1975-ben Bongard egy tanítványa, Maksimov készítette. Ez a program valójában nem Bongard problémákat oldott meg, hanem az azokhoz nagyon hasonló, 48 “Maksimov problémát” (a továbbiakban MP). Bemenetként 45x64 pixel felbontású, fekete-fehér képeket használt. Egy MP-ben tetszőleges számú kép lehet a bal és a jobb oldalon, amikhez egy megkülönbözetető szabályt kell találni, illetve egy új problématípust is létrehozott, ahol a két osztály csak egy-egy mintapéldánnyal adott, és az alattuk lévő többi kép közül kell kiválogatni a kategóriákba illőket. Ha a program mindig visszajelzést kap egy embertől, hogy helyesen választott-e, akkor egy tanulási folyamat valósul meg.
Maksimov az akkoriban elfogadott általános MI filozófiai megközelítést alkalmazta, vagyis a problémákat egy állapottérként fogta fel, ahol valamilyen heurisztika szerint kell az állapotokon a cél felé haladni, hogy az exponenciális idő és tárigényt csökkentse. A képekből egy fa gráfot épített, ahol az eredeti kép a gyökér, ebből különböző műveletekkel származtat le új képeket, amikre rekurzívan ugyanezeket a műveleteket alkalmazza. Ilyen művelet a csak körvonalak meghagyása, minden körvonal kitöltése, konvex burok, elemek szétválasztása. Közben numerikus és logikai értékeket rendel a képekhez, úgy mint terület (pixelek száma), kerület, konvexitás, kitöltöttség. Az eljárás akkor ér véget, ha elér egy olyan állapotot, ahol a bal oldali képek egyik értéke minden képre megegyezik, de a jobb oldali képekétől különböző.
Maksimov állítása szerint a program által elért eredmények hasonlítanak az emberi eredményekhez, bár nem ad részletes adatokat erről. Az MP-k megoldásai azonban általában olyanok, amik egy gép számára könnyen megtalálhatók ezzel az algoritmussal, de embereknek kevésbé kézenfekvők (pl. konvex burok kerülete). A másik probléma, hogy az akkori gépek memóriája nem volt elég nagy a leszármaztatott fa tárolásához, így sokszor el kellett dobni adatokat, amik lehet hogy később hasznosak lettek volna.
Egy teljesen más megközelítésre épülő programot 1993-ban Saito és Nakano publikált [3]. Ez az RF4, ami általános logikai problémamegoldásra készült, és többek közt a Bongard problémák világában is kipróbálták. Az eredményekről annyit árultak el, hogy a 100 BP-ből 41-et oldott meg. Ennek a programnak a bemenetei azonban nem a képek pixelei, hanem egy logikai formula, amit valakinek előre el kell készítenie. Az algoritmus elsőrendű logikai formulák terében dolgozik, amit mélységi kereséssel jár be, dinamikusan változó sorrendben. Egy működési ciklus során új alapformulát generál, amit különböző feltételek alapján eldob, vagy megtart. Ha nem dobja el, akkor kombinálja a korábbi formulákkal, amig ez a transzformációkkal lehetséges. Ha nincs több kombináció és még nem találta meg a megoldást, új alapformulát generál. Képes tanulásra is, amit bizonyít, hogy mikor másodszorra oldotta meg ugyanazokat a problémákat, a megoldás csak harmadannyi időt vett igénybe.
BP 6-nál a bal fölső ábra reprezentációja logikai formulákkal:
sokszög(X) ^ üres(X) ^ szögek(X) = 3
A probléma megoldása pedig ez lesz:
Ez a megközelítés nem mindig működik, mert sok információt elhagy, például a háromszög pozícióját a dobozon belül, pedig van ahol ez a megoldás kulcsa. Ha hozzávesszük ezt az információt a leíráshoz, így fog kinézni: sokszög(X) ^ üres(X) ^ szögek(X) = 3 ^ súlypont(X) = P
Hasonlóan hozzá kellene venni még a háromszög szélességét, magasságát, területét, stb. Fellépnek azok a problémák is, melyeket írásom korábbi részében mutattam be, például hogy bizonyos esetekben egy háromszöget három vonalként kell értelmezni. Vannak esetek, amikor egy zárt görbe alakja nem lényeges, mert csak a belső és külső tartomány számít, az RF4 ezt zárt_görbe(X) formában írja le. Azonban más esetek is vannak, amikor szabálytalan alakú zárt görbe szerepel a képen, de az alakja nem elhagyható információ, ekkor hosszabb leírást kell készíteni. Tehát két lehetőség van: vagy minden információt felhasználó leírást készítünk, ami túl hosszú és nehezen kezelhető, vagy elhagyunk fontos információkat, és bizonyos problémákat nem tudunk megoldani.
Harry Foundalis ebből azt a következtetést vonja le, hogy a logikai formulák nem alkalmasak a Bongard problémák megoldására [4]. Az RF4 csak úgy tud hatékonyan működni, ha egy olyan ember készíti el számára az ábrák reprezentációját, aki már tudja a megoldást. Hiányzik belőle az a fontos képesség is, hogy ha zsákutcába ér a program, új nézőpontból vizsgálja meg a problémát.
1996-ban Harry Foundalis egy teljesen új megközelítést alkalmazva készítette el kifejezetten Bongard problémák megoldására a Phaeaco-t [4]. Ugyan kevesebb BP-t tudott megoldani, de az RF4-gyel ellentétben nem igényel előfeldolgozást, bemenetként 12 darab 100x100 pixel felbontású fekete-fehér képet kap, két osztályra bontva. A problémamegoldás két szinten történik, először az összes képet egyszerre látja a program, ennek alapján néhány megoldási “ötlete” támad, amiknek az alkalmazhatóságát részletesen megvizsgálja minden egyes képre. Nem lehet előre tudni, hogy milyen ötletei lesznek a programnak az első fázisban, ezért egy BP-t csak az esetek bizonyos százalékában tud megoldani.
Egy probléma csoport amiben a program sikeres, amikor valamilyen tulajdonság értéke különböző a két oldalon, mint BP 3 esetén, amit a leggyorsabban tud megoldani. Itt a tulajdonság a kitöltöttség, ami igaz vagy hamis lehet, ezért az egyezés nagyon gyorsan kiderül, és nincs szükség a második fázisba lépésre. Ugyanígy működik a folytonos értéket felvevő tulajdonságokra is, például BP 2-nél. Az első szinten statisztika készül a területekről, és mivel ez jelentősen eltér, a programnak az lesz az ötlete, hogy a megoldás a területekhez kapcsolódik. Itt belép a második fázisba, minden képre kiszámolja az objektum pontos területét, és ezzel megtalálja a megoldást.
További sikeresen megoldott BP csoport a számosságra épülők (egy objektum – két objektum, három vonal – öt vonal), illetve a létezéssel kapcsolatosak (egyik oldalon van görbe szakasz, a másikon nincs). Kisebb valószínűséggel oldja meg a program a konvex burok vizsgálatát igénylő problémákat, mert a konvex burok képzése viszonylag lassú művelet, ezért nem mindig hajtódik végre, csak ha az első fázis ezt javasolja a másodiknak.
Magasabb szintű absztrakciós gondolkodást igényelnek azok a BP-k, ahol a hasonlóság nem tulajdonságok, hanem tulajdonságok kapcsolatai között áll fenn (egy képen egyforma méretű objektumok – különböző méretűek). Itt a Phaeaco eredményei jóval gyengébbek, mint az embereké. Ez volt az egyetlen olyan problématípus, ahol miután a programozó beépítette a megoldáshoz szükséges képességeket, két másik probléma is automatikusan megoldódott. Ennek az az oka, hogy Bongard igyekezett elkerülni az ismétlődést, a problémái szinte mind egy új ötletet használnak fel. 100x100 pixeles képeken azonban nyilván nem lehet végtelen sok problémát ábrázolni, ezért elméletben ha mindig új feladatok megoldására teszünk képessé egy programot, végül mindent meg tud majd oldani.
A Phaeaco tartalmaz egy “mentor” funkciót is, aminek segítségével egy ember alakzatokra tudja tanítani. Ez úgy történik, hogy egy dobozban rajzot készít róla, és beírja a nevét, ami lehet egy szó vagy egy egész mondat is. Ezután a program elemzi és tárolja a rajzot, a szöveget pedig megkísérli morfémákra bontani, és asszociációkat hoz létre a kettő között. Így lehetséges az, hogy a program kezdetben nem ismer egy olyan egyszerű fogalmat sem, mint a háromszög.
A Phaeaco által megoldott problémák száma ugyan kisebb, mint néhány más hasonló célú programé, azonban magas automatizálási szinten áll, vagyis minimális emberi segítséget igényel.
Az eredeti, 100 darab Bongard által készített problémához elsőként Douglas Hofstadter adott hozzá 56 új problémát, majd Harry Foundalis 44-et. Ma már több, mint 300 különböző példány létezik. A megoldásuk formája alapján több csoportba sorolhatók, többek közt:
-
tulajdonság értéke (kitöltöttség, terület, számosság)
-
tulajdonság értékeinek kapcsolata (azonos, különböző)
-
létezés
-
szerkezet és relációk
A fentieken kívül az MI számos területét érinti egy-egy feladvány, ami magyarázatot ad arra, hogy miért jelent még mindig komoly kihívást egy megoldó program készítése, miközben egyes emberek elegendő gondolkodási idő után a legtöbb problémára jól válaszolnak. Néhány példa:
-
BP 100: karakterfelismerés
-
BP 121: kódolás
-
BP 90, 166: klaszterezés
-
BP 170: asszociáció
-
BP 176: útkeresés
-
BP 195: térlátás
-
BP 198: mozgás
-
BP 199: gravitáció
-
BP 200: Bongard probléma a Bongard problémák megoldási módszereiből
-
BP 252: lehetetlen testek
Az összes BP megtekinthető az [5] forrásként megadott honlapon.
Ezek után felmerül a kérdés, hogy szükséges-e ezeknek a fogalmaknak az előismerete a valós világból. Ugyanis ha így van, az lehetetlenné teszi egy tökéletes megoldóprogram létrehozását. Időnként jelentősen befolyásolja az embereket a képek leírásában a valós világ béli objektumokkal szerzett tapasztalat és a matematikai fogalmak ismerete. Könnyebben oldják meg például a konvex és konkáv fogalmakra épülő feladatokat azok az emberek, akik ismerik őket, és valószínűleg aki soha nem látott fát, az nehezebbnek találná BP 70-et. Sajnos ezt a kérdést nem tudjuk eldönteni, mert az emberi agyban nem lehet különválasztani az előismereteket a gondolkodástól. Hofstadter szerint azonban nincs szükség semmilyen előismeretre, vagyis ha létezik a tiszta, minden mástól független intelligencia, akkor a Bongard problémák ahhoz nagyon közel állnak [2].
[1] Alexandre Linhares: A glimpse at the metaphysics of Bongard problems; Artificial Intelligence, Volume 121. Issue 1-2., Aug 2000.
[2] Douglas R. Hofstadter: Gödel, Escher, Bach: An eternal golden braid; Basic Books, New York, 1979.
[3] Kazumi Saito and Ryohei Nakano: A Concept Learning Algorithm with Adaptive Search in Proceedings of the Machine Intelligence 14 Workshop, pp. 347–36, Oxford University Press, New York, 1993.
[4] Harry E. Foundalis: Phaeaco: A cognitive architecture inspired by Bongard’s problems
; PhD. Thesis, Indiana University, May 2006.
[5] Harry Foundalis - Index of Bongard Problems
Szerző: Korom-Vellás Judit, BME
Allen Newell és Herbert Simon által javasolt un. fizikai szimbólumrendszer és heurisztikus keresés hipotézisek analitikus és egyben szintetikus paradigmák intelligensen viselkedő rendszerek tanulmányozásához (analitikus paradigma a meglévő rendszerek elemzésének eszköze, szintetikus paradigma pedig az új rendszerek megtervezésének eszköze). Akármennyire manapság több támadás is érte őket, vitatatlan érdemük, hogy e hipotézisek szilárd empirikus alapokra fektették a számítógépes tudományokat, ezen belül a mesterséges intelligenciát. Tudományos hipotézisek, és ha tetszik, ha nem, komoly vetélytársuk azóta nemigen született meg.
A fizikai szimbólumrendszer hipotézis forrása annak a ténynek a felismerése, hogy a számítógépes tudományok valóban (a formális módszerekbe és a formális verifikálásba fektetett minden bizalmunk ellenére) empirikus tudományok, ahol minden számítógépes fejlesztés, programkészítés, implementáció, üzembe helyezés, egy tudományos kísérlet is egyben. Ritkán bízhatunk abban, hogy a rendszerspecifikáció képes magába foglalni a rendszer működésének és használatának minden, legapróbb mozzanatát, főleg akkor, amikor a rendszer alkalmazási környezetéről eleve hiányos és elavult információval rendelkezünk. Ha viszont empirikus tudománnyal van dolgunk, szükséges valami átfogó paradigma, hipotézis, amely az empirikus kutatásoknak rendszerességet, gerincet kölcsönöz.
Az empirikusan felfogott számítógépes tudományoknak speciális vonása, hogy a vizsgált termékek – az alkalmazott számítógépes rendszerek – nem égből pottyant akármik, hanem általunk megtervezett, átlátott rendszerek. Rendszertechnikai szaknyelven nem fekete, hanem erősen fehér dobozok. Ez tehermentesít minket, hogy az empirikus értékeléseknél igénybe vegyük a statisztikát és a nagy számok törvényét. Elegendő egyetlenegy megtervezett rendszer tanúsága adott körülmények között, hogy a tervezési elképzeléseink sikerességéről helyes képet megalkothassunk.
Számítógépes tudományokban az empirikus paradigmának hasonló szerepet kell betöltenie, mint amilyen a sejtparadigma biológiában (minden élő szervezet sejtekből épül fel), a tektonikus lemez paradigma geológiában (koncepcionálisan minden levezethető lemezek egymáshoz képesti mozgásából), a bakteriális kórokozó paradigma orvosi tudományokban (minden betegség oka egy nem látható bacilus törzs), ill. az atomisztikus paradigma a modern fizikában és kémiában. A paradigma lényege, hogy támpontot szolgál specifikusabb tudományos kérdések megfogalmazásához és empirikus kísérletek megtervezéséhez e kérdések eldöntéséhez. Ilyen paradigmát keresünk az empirikus számítógépes tudomány számára.
A mesterséges intelligencia feladata lenne az intelligenciának számítási modellekkel való megvalósítása, azonban intelligencia összetett, nincs olyan dolog, ami önmagában felelős lenne intelligenciáért annak minden megnyilvánulásában. A rendszer intelligenciáját abban a képességben szokás látni, vagy ezzel a képességgel mérni, ahogy a rendszer a kitűzött célokat éri el a környezete által mutatott változások, nehézségek, és komplexitások ellenére (ld. racionalitás kérdése). Ez nyilván nem fedi az intelligencia összes lehetséges megnyilvánulását, de ez a megközelítés kellően széles és gazdag, hogy akár az emberi, akár a gépi viselkedés terén lehetőséget teremtsen pragmatikusan fontos kérdések tanulmányozásához. Az egyik ilyen kérdés az intelligens viselkedés és a szimbolikus információ kezelésének a viszonya.
A hipotézisek megalkotói szerint a szimbólumokat tárolni és manipulálni képesség megléte az intelligenciához vezető egyik alapvető kívánalom. Mielőtt magát a hipotézist megfogalmazzuk, ildomos tisztázni a benne szereplő fogalmakat. Fizikai szimbólumrendszerről fogunk beszélni, azaz olyan rendszerről, amely engedelmeskedik fizika törvényeinek (és netán mérnökök által is megvalósítható, mert a szimbólumok kezelése nem korlátozódik emberre). A rendszer tartalma a fizikai mintázatok által képviselt szimbólumok halmaza, melyek bonyolultabb szimbólum struktúráknak – kifejezéseknek – az elemei. Adott pillanatban a rendszer tartalmaz szimbolikus struktúrákat és folyamatokat, amik a struktúrákon operálnak, kifejezéseket létesítenek, módosítanak, reprodukálnak, ill. megsemmisítenek. A fizikai szimbólumrendszer tehát egy gépezet, amely időben változó szimbólum struktúrákat gyárt.
A szimbolikus információ használatánál központi fogalom a megjelölés és az interpretáció. Egy kifejezés megjelöl egy objektumot, ha a kifejezés birtokában a rendszer képes az objektumot befolyásolni, vagy objektumfüggő módon viselkedik. A rendszer egy kifejezést interpretál, ha a kifejezés egy folyamatot megjelöl, és ha a kifejezés birtokában a rendszer a folyamatot végrehajthatja. Szükséges még kijelenteni, hogy a kifejezések stabilak. Ha egyszer létesültek, fennmaradnak, amíg explicit módon nem lesznek módosítva. Tételezzük azt is, hogy a kifejezések száma lényegében korlátlan.
Ezek után megfogalmazható már a Fizikai Szimbólumrendszer (FSzR) Hipotézise, miszerint:
„a fizikai szimbólumrendszer szükséges és elégséges eszközökkel rendelkezik az általános intelligens viselkedés megvalósításához”.
A „szükséges” azt a sejtést takarja, hogy minden általánosan intelligens rendszer, ha tüzetesebben megvizsgáljuk, kiderül, hogy egy FSzR. Az „elégséges” arra utal, hogy minden FSzR, ha már kellően gazdag és bonyolult, megszervezhető úgy, hogy az általános intelligens viselkedést felmutassa. (Itt az általános intelligensen – ugyanúgy, mint az embernél, akármilyen valós viselkedést kell érteni, ami a célokkal adekvát, a környezeti kívánalmakkal szemben adaptív, és ez mind a komplexitás és a sebesség korlátain belül. E megfogalmazás alapvető fontossága, hogy az intelligens cselekvést annak eredménye alapján ismerjük fel, függetlenül attól, hogy emberi eredetű, vagy sem.)
A FSzR hipotézis sokak által vitatott (ld. a könyv 26. fejezete) folyománya, hogy az intelligenciát univerzális számítógépen meg lehet valósítani (ennek történelmi lépcsői a formális logika megszületése, a Turing gép gondolata és a digitális számítógép megjelenése, majd képességeiben rohamos fejlődése a tárolt program, listakezelés, stb. mérföldkő ötletek nyomán).
A FSzR hipotézis megalkotói szerint a FSzR alapvető működési folyamata a heurisztikus keresés, amit a Heurisztikus Keresés Hipotéziseként fogalmaznak –
„A FSzR-en belül a problémák megoldását szimbolikus struktúrákként reprezentáljuk és a FSzR keresés révén mutatja fel a problémamegoldó intelligenciáját – folyamatos generál és módosít szimbolikus struktúrákat, amíg rá nem fut a megoldásra”
– és a problémamegoldásban az intelligens viselkedés egyik elsődleges jellemzőjét látják. Problémamegoldáshoz elengedhetetlen a probléma megfogalmazása, aminek elemei egy teszt a megoldást jelentő szimbolikus struktúrák észlelésére és a potenciális megoldásokat jelentő szimbolikus struktúrák (lépés)generátora. Problémát megoldani azt jelenti, hogy egy olyan szimbolikus struktúrát képesek vagyunk generátorral generálni, ami teljesíti a megoldástesztet. Nyilvánvaló, hogy a probléma (akkor) létezik, ha tudjuk, mire van szükségünk (ez a teszt), de a megoldását nem tudjuk azonnal létesíteni (generátor valamilyen értelemben nem tökéletes).
A kigenerált, a teszten elbukott, de várhatóan még hasznos struktúrák (problémahelyzetek) tárolásához problématérre van szükség, ahol többek között helyezkednek a probléma kezdeti és a célhelyzete. A FSzR korábban említett hipotetikus tulajdonságai garantálják, hogy problémamegoldó mechanizmus gyanánt felépíthetünk benne a problémateret a lépésgenerátorával együtt.
Problématér paradigma felül megközelítve az intelligencia kérdését azt mondhatjuk, hogy ha a rendszer képes kontrollálni, hogy a generált probléma helyzetek milyen sorrendben kerülnek tesztelésre, akkor kívánatos lenne olyanokkal kezdeni, amelyek nagyobb valószínűséggel garantálják a megoldás korai megjelenését. Egy FSzR-t annyiban tekinthető intelligensnek, amennyire ezt a fajta működést képes megvalósítani. Fontoljuk meg mi lehetne ennek (avagy az intelligencia megjelenésének) a feltétele?
A válasz egyszerűen hangzik, ám konkrét körülmények között a megvalósítása akár a lehetetlenség határát súrolja. Szimbolikus struktúrák (probléma) terének valami mintázatot, rendezettséget fel kell mutatnia, nem lehet „ránézésre” tökéletesen véletlen, és ennek a mintázatnak detektálhatónak kell lennie. Azaz kell, hogy a problématérben beágyazva legyen valamilyen információ, amit a FSzR képes kiemelni és felhasználni, és azáltal mérsékelni a heurisztikus keresés mértékét. Komplexitás szempontjából a problémák lényege nem a kevés, vagy a sok keresés, ami a megoldásukhoz szükséges, de inkább az a sok keresés, ami a megoldásukhoz szükséges lenne, ha a rendszer a megfelelő intelligenciaszintre felkapaszkodni nem tudna. Az intelligencia „informatikai” feladata így a keresés exponenciális robbanásának veszélyét kivédeni, eltávolítani. Ennek kapcsán beszélünk gyenge – a buta exponenciális keresést kivédeni nem képes – és erős – a keresés igényét legalább elvben erőteljesen mérsékelő – módszerekről.
Hogyan juthatunk „informatív”, erős és kiaknázható mintázatot felmutató problématérhez? Erre választ ad a tudásreprezentációk kutatása. Megfelelő tudásreprezentáció megválasztása a problémát olyan problématérbe absztrahálja, ahol hatékony a lépésgenerálás kontrollja és rövidebb (intelligensebb) a megoldás folyamata. Kirívó esetekben az absztrakció annyira jól is sikerülhet, hogy a keresést teljes egészében el lehet kerülni. Előfordul fordítva is, hogy az erőteljes absztrakciók nem vezetnek eredményre, de a technológia előrehaladása és a számítások gyorsítása lehetőséget teremt a sok kereséssel korábban büntető egyszerűbb problématérbe visszalépni és a korábban fel nem vállalható keresési volument kivárva, a problémát sikerrel megoldani (Ez történt tulajdonképpen a sakkban, Deep Blue, ill. korábban még a dámajáték esetében a Chinook kifejlesztésével. Go esetén azonban a helyzet továbbá is reménytelen).
Az említett hipotézisek természetesen hamisak is lehetnek. A FSzR hipotézist érő kritikák jó összefoglalója a Wikipedia cikk. Azonban lássuk be, hogy mielőtt foglalkoznánk, hogy egy hipotézis igaz, vagy hamis, érdemes terítékre venni, hogy releváns-e (tudományosan hasznos)? Egy hipotézis releváns, ha világosan megadja, hogyan kellene azt verifikálni és a tesztekben hol kellene látni a hipotézis sikerét, vagy bukását. Az FSzR és a HK hipotézisek mindegyike releváns. Igazak-e? Építsük egyre bonyolultabb fizikai szimbólumrendszereket és értékeljük a viselkedésüket! Ugye egyszerű!
Fontos azt is kihangsúlyozni, hogy az eltelt 35 év ellenére mégsem született meg hasonló általánossággal megfogalmazott, tudományosan releváns hipotézis vetélytárs. Az „intelligencia szimbólumok nélkül” kritikáknál pedig ne felejtsük, hogy:
-
lehet, hogy a futási időben nehezen látjuk ilyen rendszerekben a szimbolikus információt, de a megtervezésükhöz mindenképpen szükség volt a tervező (emberi) FSzR közreműködésére (a reflexszerű ágens programját célorientáltan deliberatív tervezőnek meg kell írnia), avagy ilyen rendszerek tulajdonképpen a „lefordított” tudást képviselnek.
-
a FSzR valóságos volta egy fizikai rendszer, a szimbólumrendszer egy leíró és egy prediktív modell a viselkedésének értékeléséhez (pl. ahhoz, hogy a fizikai valóságot milyen absztrakciós szinten fogjuk meg, hol jelenik meg a kontrollba átemelhető mintázat.). Semmilyen rendszer – fizikai révén, nem létezik egyből a szimbólum szintjén. Annak kell modellezni, hogy beszélhessünk róla (Sakkot játszunk egy teljes és egy bábu hiányos sakk készlethez. A másikhoz gyufadobozt kooptálunk fekete vezér minőségében. Mennyi fog a játék (legális sakk) mindkét esetben? Igen. Különböző a két fizikai rendszer? Igen. Azonos a szimbolikus absztrakció (problématér), a keresés mértéke? Igen.)
Newell, Allen; Simon, H. A. (1976), "Computer Science as Empirical Inquiry: Symbols and Search", Communications of the ACM, March 1976, Vol 19, No 3, pp. 113- 126 (1975 Turing Award Lecture),
http://portal.acm.org/citation.cfm?id=360022
Fizikai szimbólumrendszer hipotézis összefoglalása:
http://www.rci.rutgers.edu/~cfs/472_html/AI_SEARCH/PhysicalSymbolSystemHyp.html
Fizikai szimbólumrendszer hipotézis összefoglalása:
http://en.wikipedia.org/wiki/Physical_symbol_system
Deep Blue-val kapcsolatos oldalak:
http://www.nybooks.com/articles/archives/2010/feb/11/the-chess-master-and-the-computer/
http://www.worldchesschampions.com/kasparov_vs_deepblue.php
http://www.research.ibm.com/deepblue/learn/html/e.shtml
Chinook Home Page:
http://webdocs.cs.ualberta.ca/~chinook/
Kidolgozta: Dobrowiecki Tadeusz, BME
Készítette: Dobrowiecki Tadeusz, BME
Az 1940-es évektől kezdve egyre több tudományos kutatással kapcsolatban kerül elő a sejtautomaták fogalma. Ebben a pár oldalas esszében megpróbálom összeszedni, hogy pontosan mit is takar ez a fogalom, hogyan és mire használhatóak a sejtautomaták. Bemutatom ennek a kutatási területnek a fejlődését kezdeteitől napjainkig, külön kiemelve néhány megvalósítását és alkalmazását.
A sejtautomaták diszkrét dinamikus rendszerek, mivel helyük, idejük és állapotuk is diszkrét [ACA]. Ezt a modellt használják többek között a számításelméletben, matematikában, fizikában, elméleti biológiában és mikroszerkezet modellezésben is.
A modell egy szabályos, akár egy, vagy több dimenziós rácsozat, amelyeknek elmei cellák (sejtek). Ezeknek a sejteknek véges számú állapota lehet. Egy sejt t időbeli állapota csak a sejt t-1 időbeli állapotától, a cella szomszédainak t-1 időbeli állapotától és egy előre meghatározott (általában matematikai) szabálytól függ. Minden sejt állapota szinkronban változik, frissül. Ezt a frissülést új generáció létrejöttének nevezzük.
Többféle sejtautomata létezik, amelyeket alapvetően a dimenziójuk, és az előre meghatározott generációs szabályaik különböztetnek meg. Ilyenek például a Rule sejtautomaták (Rule 30, Rule 90 stb.), a Wireworld, a Neumann sejtautomata, és a Conway-féle életjáték, amelyek közül néhányat majd részletesebben bemutatok.
Stanisław Ulam matematikus az 1940-es években a Los Alamos-i Nemzeti Laboratóriumban kristályok növesztését tanulmányozta, egy egyszerű rácsszerkezet modellt alkalmazva. Eközben munkatársa, Neumann János az önreprodukáló rendszerek problémájával foglalkozott. Neumann eredeti felvetése az volt, hogy vajon miféle logikai szerkezet elegendő egy olyan automatikus géphez, amely önmagát reprodukálni képes. Az ilyen szerkezetet kinematikus modellnek nevezzük. A tervezés közben Neumann rájött, hogy mennyire nehéz egy magát reprodukáló robot megalkotása. Elfogadva Ulam tanácsát, a szerkezetet egy olyan matematikai absztrakció köré építette, amely egyike volt Ulam kristálynövesztési tanulmányai során használtaknak. Ebből alakult ki az első rendszere a sejtautomatáknak, amit Neumann Univerzális Konstruktorának neveznek [TJN].
1946-ban Norbert Wienernek és Arturo Rosenblueth-nak jelent meg „The mathematical formulation of the problem of conduction of impulses in a network of connected excitable elements, specifically in cardiac muscle” című tanulmánya, amelyben egy olyan sejtautomata modellt alkottak meg, amely matematikai leírást adott a keringési rendszerek ingerületvezetésére. Munkájukra a későbbi szívritmuszavarral és ingerlékeny rendszerekkel foglalkozó modern kutatások is hivatkoztak.
Az 1960-as években a sejtautomatákat a dinamikus rendszerek egy típusaként tanulmányozták és először állapították meg kapcsolatát a szimbolikus dinamika területével. 1969-ben jelent meg Gustav A. Hedlund „Endomorphisms and automorphisms of the shift dynamical system” című írása, amely ebből a nézőpontból indult ki. Legalapvetőbb eredménye a sejtautomaták globális állapotainak karakterizációja, mint váltás terek folyamatos endomorfizmus halmaza.
Az 1970-es években egy kétállapotú, kétdimenziós az Élet játékának (Game of Life) nevezett sejtautomata vált ismerté, főleg a kialakuló számítógépes közösségben. Feltalálója John Horton Conway volt, ám nem ő, hanem Martin Gardner mutatta be a világnak 1970 októberében, a Scientific American című magazinban.
1969-ben jelent meg a számítástechnika német úttörőjének, Konrad Zuse-nak „Calculating Space” című műve, amelyben azt ajánlotta, hogy az univerzum fizikai törvényeire tekintsünk úgy, mint a természet által diszkretizált, óriási sejtautomata számítási eredményeinek kimenetelére. Ez volt az első könyv a digitális fizika témakörében.
1983-ban Stephen Wolfram publikálta szisztematikus vizsgálatának első sorozatát egy nagyon alapvető, de még ismeretlen sejtautomata fajtáról, amelyet ő általános sejtautomataként (elementary cellular automata) nevezett. Ezen sejtautomatára egyszerű szabályai ellenére igen komplex viselkedés volt jellemző, amely komplexitás a természetben is hasonló mechanizmusokra vezethető vissza.
2002-ben jelent meg Wolfram 1280 oldalas könyve az „A New Kind of Science”, amelyben részletesen kifejti, hogy a sejtautomatákról tett felfedezések nem elszigetelt tények, hanem valamilyen szinten minden tudománnyal kapcsolatosak [TSW].
Az általános bevezetőben már láthattuk, hogy a sejtautomatákat mennyi tudományterületen alkalmazzák. Az Interneten keresve töménytelen mennyiségben találunk tudományos munkákat, írásokat, amelyek a sejtautomaták elméleti vagy gyakorlati alkalmazásairól értekeznek.
Sejtautomatákat alkalmaznak földrajzi információs rendszereknél, az ún. pont minta analízishez, legközelebbi szomszéd analízishez. Ezzel a módszerrel elemezték Milwaukee rablóinak helyét összevetve az áldozataik címével és a Montana-i település eloszlások Voronoi diagramjait is [PVD].
Ökológia rendszerek modellezésével kapcsolatban egyre többször kerül elő a sejtautomaták fogalma, ám gyakori kérdésként merül fel, hogy egyáltalán jogos-e használatuk, főleg a modell diszkrét tulajdonsága miatt.
Sejtautomatákkal véletlen-számokat generálhatunk, és titkosíthatunk, de erről később még kicsivel részletesebben is fogok írni.
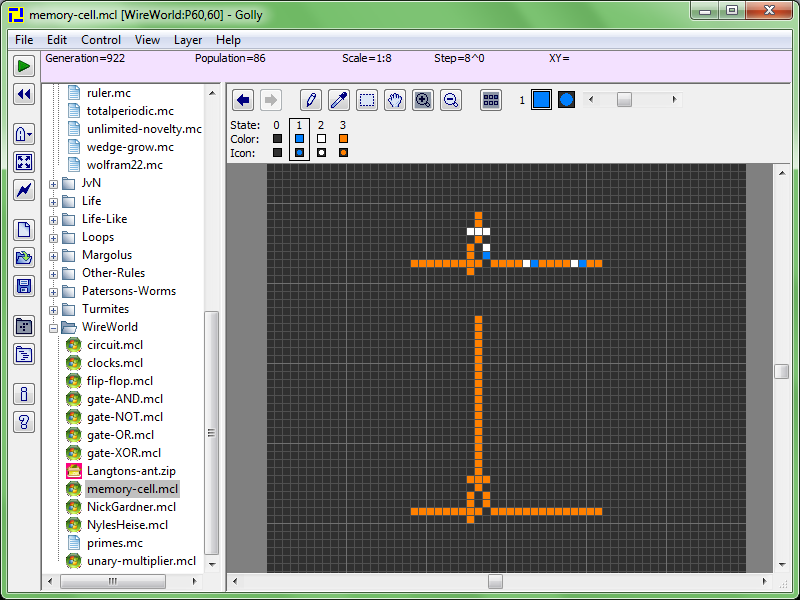
Feltehetjük a kérdést, hogy milyen számításokat lehet elvégezni egy sejtautomata segítségével. Igen érdekes választ kapunk, ha figyelembe vesszük a Wireworld nevű sejtautomatát. Ezt 1987-ben Brian Silverman mutatta be, Phantom Fish Tank nevű programjának részeként. A Wireworld elektronikus logikai elemeket, kapukat szimulál. Tudjuk, hogy a mai számítógépek alapjai ezek a kapuk, és ebből következik, hogy összeállíthatunk egy ilyen számítógépet, amivel tetszőleges számítást elvégezhetünk. Persze ne feledkezzünk meg arról, hogy ez soha nem lesz megfelelő teljesítményű [PWW].
A mesterséges intelligenciát legjobban érintő alkalmazása a sejtautomatáknak a CBM vagy CAM-Brain Machine. Ez egy hardverarchitektúra, amely képes valós időben több millió neuront tartalmazó neurális hálózatokat szimulálni [PCB].
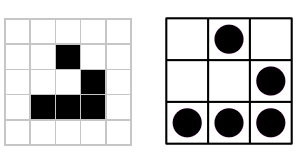
1983-ban Stephen Wolfram mutatta be a Rule 30 nevű egy dimenziós bináris sejtautomatát [KCA], amelyet A New Kind of Science című könyvében is részletez [KSW]. Wolfram osztályozását használva ez az automata 3-as osztályú, vagyis aperiodikus, kaotikus viselkedést mutat.
A Rule 30 különösen érdekes sejtautomata, mivel komplex, látszólag véletlenszerű mintázatot állít elő egyszerű, jól definiált szabályokból. Wolfram ebből a modellből kiindulva állapította meg, hogy egyszerű szabályok létrehozhatnak nagy, komplex struktúrákat és viselkedéseket a természetben is. Bizonyítékként szokták emlegetni az egyik tengeri csiga fajt, a Conus textile-t, amelyen a Rule 30 által előállított kimenethez hasonló minta található (lásd az 1. ábrát).
A Rule 30-at használja Wolfram Mathematica nevű programja véletlen-szám generáláshoz, és ebből kifolyólag kriptográfiai alkalmazása is ismert.
A sejtautomaták közül a legelső volt a Neumann-féle sejtautomata, amit Neumann János alkotott meg Stanisław Ulam javaslatára. Ebben az automatában a véges állapotgépek (vagy sejtek, cellák) egy két dimenziós, kartéziánus (Descartes koordináta rendszer alapú) rácsba vannak rendezve úgy, hogy minden cellának 4 szomszédja van. Mivel ezt a kialakítást először Neumann írta le, ezért is nevezik ezt Neumann szomszédságnak. Egy sejt 29 lehetséges állapotot vehet fel a szabályoknak megfelelően. A Neumann sejtautomata továbbfejlesztéseként jelent meg később többek között Nobili és Hutton sejtautomatája is [KNB].
1970 októberében jelent meg a világ egyik, talán legismertebb sejtautomatájának, a Conway-féle automatának leírása. Az automata igen egyszerű szabályokra épül, ám ennek ellenére izgalmas és látványos kimeneteket ad vissza.
Nevét kidolgozójáról, John Horton Conway angol matematikusról kapta. A játék nulla-játékos (zero-player), ami azt jelenti, hogy az evolúció a kezdeti kiindulóállapotból meghatározott, nincs szükség további bemenetre [GCW].
Az automata egy 2 dimenziós rácsszerkezeten alapul. A cellák kétféle állapotot vehetnek fel, lehetnek élőek vagy halottak. A szabályok a következőek:
-
Bármelyik élő sejt (cella) meghal, ha 2-nél kevesebb élő szomszédja van. (Elpusztul a magányban.)
-
Bármelyik élő sejt életben marad a következő generációban, ha 2 vagy 3 élő szomszédja van.
-
Bármelyik élő sejt meghal, ha több, mint 3 szomszédja van. (Elpusztul a tömegben.)
-
Bármelyik halott sejt életre kel, ha pontosan 3 szomszédja van. (Reprodukálódik.)
A játékból az egyik ismert kimenet a 2. ábrán látható, sikló (glider) nevű minta, amely a hacker kultúra (jobb oldali változat) [GHL] és a www.conwaylife.com
weboldal emblémája is [GGW].
Az Interneten több ezer ilyen és ehhez hasonló minta található, amelyeket a megfelelő programoknak adva bemenetként, látványos animációkat kaphatunk [GCP].
Az egyik általam legjobbnak talált ilyen alkalmazás a Golly névre hallgat [GGO]. Ez egy nyílt forrású, keresztplatformos program, amely nem csak a Conway-féle, de a már említett WireWorld és Neumann 29 állapotú sejtautomatáját is támogatja. A program a 3. ábrán látható működés közben.
A sejtautomaták az elméletből a gyakorlati alkalmazásokba is átkerültek, nem csak szoftveres, hanem hardveres implementálásokban is, amelyek közül több kereskedelmi forgalomban is kapható vagy kapható volt. 1987-ben jelent meg Tommaso Toffoli és Norman Margolus „Cellular Automata Machines” című könyve, amelyben egy ilyen hardveres megoldás részletezve van [HTM]. Ez a CAM-6 nevet viseli.
A CAM-6-ot eredetileg az MIT Laboratory for Computer Science fejlesztette ki. Később az MIT a Systems Concepts-et (a későbbi SC Group-ot) kérte fel a piaci termelésre, hogy ezzel a tudományos közösség számára is elérhető legyen.
A CAM-6 valójában egy IBM-PC, -XT, vagy -AT kompatibilis kártya, és a hozzátartozó PC-DOS 2 kompatibilis meghajtóprogram. Ezzel a koncepcióval elérték azt, hogy a PC erőforrásait (a tápot, lemezmeghajtót, monitort, az alapvető operációs környezetet) kiegészítették egy nagy sebességű sejtautomata szimulátorral, amelynek teljesítménye (erre az adott feladatra) a CRAY-1-ével volt összehasonlítható. Másodpercenként 60 sejtautomata állapotot frissített egy 256x256-os táblán. A vezérlő szoftvert Forth nyelven írták, és 256 kB memórián futott.
A CAM-6 tovább fejlesztett, kompatibilis változata a CAM-PC. 16 bites keresési táblát (lookup table) használt, és támogatta a komplex programozható futási ciklusokat, így a felhasználó többlépéses sejtautomata szabályokkal is dolgozhatott [HHG].
A legutóbbi CAM változat a CAM-8, amelyet szintén az MIT fejlesztett ki. A hardver lelkét a STEP nevű ASIC chip adta. A STEP egy skálázható, fizikai rendszer szimulációkra optimalizált multiprocesszor architektúra [HTF]. Egy STEP kártya, ami 16 db processzort tartalmazott, CBus-on keresztül kapcsolódott a rendszer többi eszközéhez. Egy CBus panelbe 8 db kártya fért, így maximum 128 CAM-8 processzorból állhatott egy számítógép.
A CAM-8-at Sun munkaállomásokban használták, a támogatott operációs rendszer a SunOS volt. Miután a SunOS támogatottsága megszűnt elkezdték Solaris-ra is fejleszteni a drivert, ám az végül nem készült el teljesen. A hardver programozására, a STEP vezérlő program megvalósítására továbbra is főleg a Forth nyelvet használták, de más nyelvekkel is elkezdtek kísérletezni, mint például a Pythonnal, ám ezen próbálkozások 1998 vége felé elhaltak.
Napjainkban főleg FPGA alapú megvalósításokat alkalmaznak. Erre jó példa a már említett CBM (CAM-Brain Machine). A CBM 3D-s sejtautomatáinak hardveres megvalósítását Xilinx's XC6264 FPGA chippekkel végzik. Teljesítményét jól jellemzi, hogy másodpercenként 25 állapotfrissítést végez több millió neuronon.
A sejtautomaták egyik leggyakorlatiasabb alkalmazási területe a titkosítás tudománya, vagyis a kriptográfia. 1986-ban jelentek meg Wolfram véletlen-szám generálással [CRS] és titkosítással kapcsolatos, sejtautomatákról szóló cikkei [CCC]. Észrevehetjük, hogy már a kutatások elején megjelent ez az alkalmazás, amely főleg az automaták véletlenszerűségével, és nem mellékesen könnyű hardveres implementálásukkal magyarázható.
Sejtautomatákat használhatunk szimmetrikus kulcsú titkosításhoz, a Vernam titkosíráson alapulva [CSK]. Az automatákat, ahogyan azt már említettem véletlen-számokból álló sorozatok, szekvenciák (PNS pseudo-random numbers sequence) generálására is használhatjuk, amelyeket a titkosítás során használunk fel. A PNS-ek minősége (vagyis hogy „mennyire véletlen” az a véletlen szám) nagyban függ a sejtautomatában alkalmazott szabályoktól. A sejt programozásnak (cellular programming) nevezett evolúciós technika felfedezése során találtak olyan szabályhalmazt, amely jó minőségű titkosítást, vagyis nagy kulcs törési ellenállást biztosít.
Ennek ellenére nem bízhatunk meg teljesen ezekben a titkosítási rendszerekben. A fenti módszerrel szinte egy időben jelent meg olyan cikk, amely éppen a sejtautomatákon alapuló kriptográfiai rendszerek gyengeségét mutatja meg [CFB].
Ezzel a rövid írással próbáltam bemutatni a sejtautomaták fontosabb jellemzőit, és ebből a rövidségből következik, hogy közel se alaposan. 6 évvel ezelőtt mikor először találkoztam a Conway-féle játékkal, még nem is gondoltam, hogy mennyire komoly tudomány van a sejtautomaták mögött.
Napjainkban is nagyon kedvelt kutatási téma a sejtautomaták köre, és az elért eredmények fényében ez valószínűleg továbbra is igaz lesz, hiszen nem egy problémát sikerült megoldani az automaták segítségével. Talán a nem is olyan távoli jövőben a sejtautomaták alapvető építő elemei lesznek a mesterséges intelligenciának és tudatnak, vagy csak egyszerűen a segítségével a legapróbb részletekig megismerjük a Világegyetemet.
[ACA]
Tim Tyler, Howard Gutowitz
Cellular Automata FAQ internetes oldal
[TJN]
John von Neumann, 1951, "The general and logical theory of automata" in L.A. Jeffress, ed., Cerebral Mechanisms in Behavior – The Hixon Symposium, New York, John Wiley & Sons, 1-31
[TSW]
Stephen Wolfram, 2002, A New Kind of Science, Champaign, Wolfram Media
[PVD]
K. Sugihara, A. Okabe, and B. Boots, 1992, Spatial Tessellations: Concepts and Applications of Voronoi Diagrams, Chichester, New York, Brisbane, Toronto, Singapore, J. Wiley & Sons
[PWW]
A. K. Dewdney, 1990 Jan, "The cellular automata programs that create wireworld, rugworld and other diversions" in Computer Recreations, Scientific American, 146-149
[PCB]
Michael Korkin, Hugo de Garis, Felix Gers, Hitoshi Hemmi, 2001, "CBM (CAM-BRAIN MACHINE)" A Hardware Tool which Evolves a Neural Net Module in a Fraction of a Second and Runs a Million Neuron Artificial Brain in Real Time
[KCA]
Stephen Wolfram, 1983, Cellular Automata
[KSW]
Stephen Wolfram, 2002, A New Kind of Science
, Champaign, Wolfram Media
[KNB]
Von Neumann, J. and A. W. Burks, 1966, Theory of self-reproducing automata, Urbana, University of Illinois Press
[GCW]
[GHL]
Eric S. Raymond
The Glider: A Universal Hacker Emblem
[GGW]
A conwaylife.com oldalon található Glider szócikk
[GCP]
A conwaylife.com oldalon található minták gyűjteménye
[GGO]
A Golly honlapja a Sourceforge.net-en
[HTM]
Tommaso Toffoli, Norman Margolus, 1987, Cellular Automata Machines – A New Environment for Modeling, MIT Press
[HHG]
Howard Gutowitz, 1991, Cellular automata: theory and experiment, MIT Press
[HTF]
MIT Laboratory for Computer Science, 1993, Step Technical Reference
[CRS]
Stephen Wolfram, 1986, Random Sequence Generation by Cellular Automata
[CCC]
Stephen Wolfram, 1986, Cryptography with Cellular Automata
[CSK]
Franciszek Seredynski, Pascal Bouvry, Albert Y. Zomaya, 2003, Cellular automata computations and secret key cryptography
[CFB]
Feng Bao, 2004, Cryptanalysis of a Partially Known Cellular Automata Cryptosystem
Szerző: Nádudvari György, BME