Eddig egy időpontban csak egy képpel foglalkoztunk. A videokamerák azonban másodpercenként 30 képkockát rögzítenek, és a kockák közötti különbségek fontos információk forrásai lehetnek. Abban az esetben, ha a kamera a háromdimenziós jelenethez képest mozog, a képen keletkező látszólagos mozgást optikai folyamnak (optical flow) nevezzük. A folyam a képbeli jellegzetességek mozgásirányát és mozgási sebességét írja le, amit a jelenet és a megfigyelő egymáshoz viszonyított relatív mozgásának következtében kapunk. A 24.7. (a) és (b) ábrán egy forgó Rubik-kockát ábrázoló videofelvételből látunk két filmkockát. A (c) képen az előbbi képekből számított optikai folyam vektorai láthatók. Az optikai folyam a jelenet struktúrájára nézve tartalmaz hasznos információt. Például egy mozgó kocsiból kinézve a távoli tárgyaknak sokkal lassúbb a látszólagos mozgása, mint a közelieknek, így a látszólagos mozgás üteme a távolságról is hordoz valamiféle információt.

Az optikai folyam vektormezeje az x irányú v_x(x, y) és az y irányú v_y(x, y) komponensekkel jellemezhető. Ahhoz, hogy az optikai folyamot megmérhessük, meg kell találni az egymásnak megfelelő pontokat a szomszédos képkockákon. Ehhez azt a tényt használjuk fel, hogy az egymásnak megfelelő pontok körüli képrészeknek hasonló a fényességmintázata. Tekintsük a p, (x₀, y₀) képpont körül t₀ időpillanatban csoportosuló képponttömböt. Ezt a tömböt a t₀ + D_t időpillanatban a különböző (x₀ + D_x, y₀ + D_y) pozíciójú q_i képpontjelöltek körül csoportosuló képponttömbökkel össze kell hasonlítani. A hasonlóság egyik szóba jöhető mértéke a különbségek négyzetösszege (sum of squared differences, SSD):

24.7. ábra - (a) Rubik-kocka egy forgó lemezkorongon. (b) Ugyanaz a kocka 19/30 másodperccel később (Richard Szeliski nyomán). (c) Az (a) és (b) képek összehasonlítása alapján számolt optikai folyam vektorok (Joe Weber és Jitendra Malik hozzájárulásával).

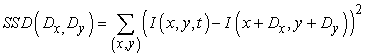
Az (x, y) az (x₀ , y₀) képpont körüli tömb képpontjainak halmazán fut végig. Megkeressük most azt a (D_x, D_y)-t, amely az SSD-t minimizálja. Az (x₀ , y₀)-beli optikai folyam ilyenkor: (v_x , v_y) = (D_x/D_t, D_y/D_t). Alternatívaként maximalizálhatjuk a keresztkorrelációt (cross-correlation):

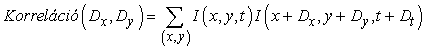
A keresztkorreláció akkor használható a legjobban, ha a jelenet képében textúra található, mert ekkor a vizsgált ablakokban nagy a fényességváltozás a képpontok mentén. Ha egy egyenletesen fehér falra nézünk, a különböző q jelöltekre számított keresztkorreláció majdnem azonos lesz, és az algoritmus a gyakorlatban véletlenszerűen fog választani.

Tegyük fel, hogy a megfigyelő T transzlációs és szögsebességgel rendelkezik [amelyek így a sajátmozgást (egomotion) írják le]. Származtatni lehet olyan összefüggéseket, amelyek a megfigyelő sebességét, az optikai folyamot és a jelenet tárgyainak a pozícióját kapcsolják össze. Tegyük fel, hogy f = 1, akkor:

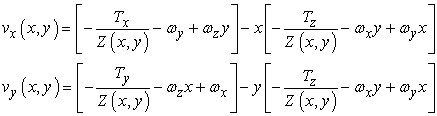
ahol Z(x, y) az (x, y) képponthoz tartozó jelenetbeli pontnak a z koordinátája.

A képlet jobb megértését szolgálja, ha az egyszerű transzláció esetét nézzük. Ebben az esetben a folyammező:

lesz. Néhány érdekes tulajdonságot figyelhetünk meg. Az optikai folyam mindkét komponense, v_x(x, y) és v_y(x, y) is zérus az x = T_x/T_z, y = T_y/T_z pontban. Ezt a pontot a folyammező expanziófókuszának (focus of expansion) nevezzük. Tegyük fel, hogy az x – y sík origóját az expanziófókuszba helyezzük át. Ilyenkor az optikai folyam kifejezései igen egyszerű formát öltenek. Jelölje (x', y') az x' = x – T_x /T_z, és az y' = y – T_y /T_z által definiált új koordinátákat. Ekkor:

Ennek az egyenletnek van néhány érdekes alkalmazása. Tegyük fel, hogy ön egy légy, amely egy falra próbál leszállni, és azt szeretné tudni, hogy adott aktuális sebesség mellett mennyi idő múlva ér a falhoz. Ezt az időt a Z/T_z adja meg. Figyeljük meg, hogy annak ellenére, hogy a pillanatnyi optikai folyam nem képes sem a Z távolságot, sem a T_z sebességi komponenst megadni, a kettő arányát meg tudja adni, és így a leszállás irányításában felhasználható. Az élő legyekkel való kísérletek alátámasztják, hogy a legyek pontosan ezt a mechanizmust használjak. A legyek a legmerészebb repülők az állatok és gépek között, és érdekes, hogy ezt egy olyan látórendszerrel teszik, amelynek borzasztóan gyenge a térbeli felbontása (körülbelül 600 érzékelője van, összehasonlítva az emberek 100 milliójával), de kiemelkedő az időbeli felbontása.

24.8. ábra - (a) Egy olyan videokép-sorozat négy kockája, amelyben a kamera a tárgyhoz képest mozgott és forgott. (b) A sorozat első képkockája, amelyen apró négyzetek jelzik a tulajdonságfelismerő által megtalált tulajdonságokat (Carlo Tomasi hozzájárulásával).

24.9. ábra - (a) A 24.8. ábrán látható kép tulajdonságai elhelyezkedésének háromdimenziós rekonstrukciója. (b) A valódi ház ugyanabból a perspektívából.

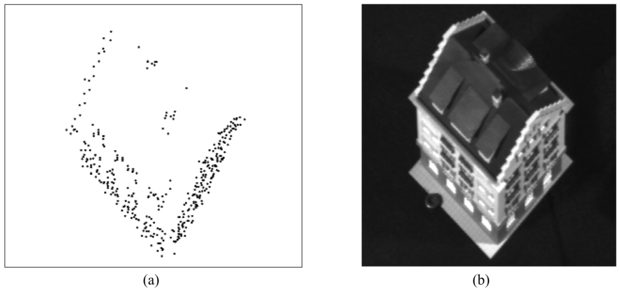
A mélység kiszámításához több képkocka használata szükséges. Ha a filmre egy merev testet veszünk fel, akkor ennek alakja képkockáról képkockára nem fog változni, és így az optikai folyam természeténél fogva zajos méréseit jobban kezelhetjük. Az egyik ilyen megközelítés eredményét a 24.8. és a 24.9. ábrán láthatjuk (Tomasi és Kanade, 1992).

A legtöbb gerincesnek két szeme van. Ez hasznos redundancia arra az esetre, ha elveszítené az egyiket, de más módon is segít. A legtöbb zsákmányállatnak a feje oldalán vannak a szemei, hogy nagyobb területet beláthasson. A ragadozóknak elöl, hogy kétkamerás térbeli látást (binocular stereopsis) valósíthassanak meg. Maga a gondolat a mozgási parallaxisra igen hasonlít, azonban az eltérő időpontokhoz tartozó képek helyett két (vagy több), térben szeparált képet használunk, hasonlóan ahhoz, mint amilyeneket pl. az előrenéző emberi szemek szolgáltatnak. Tekintettel arra, hogy a jelenet egy adott jellemzője az egyes képsíkok z koordinátájához képest más helyen lesz a képen, ha a két képet egymásra fektetjük, a képjellemző elhelyezkedésében a két kép különbséget – diszparitást (disparity) – fog mutatni. Ez látszik a 24.10. ábrán, ahol a piramis legközelebbi pontja balra mozdult el a jobb oldali képen, és jobbra a bal oldalin.

24. ábra - A térbeli látás alapgondolata: különböző kamerapozíciók ugyanannak a háromdimenziós jelenetnek kissé eltérő kétdimenziós nézeteit eredményezik

24.11. ábra - A diszparitás és a mélység összefüggése a sztereolátásban

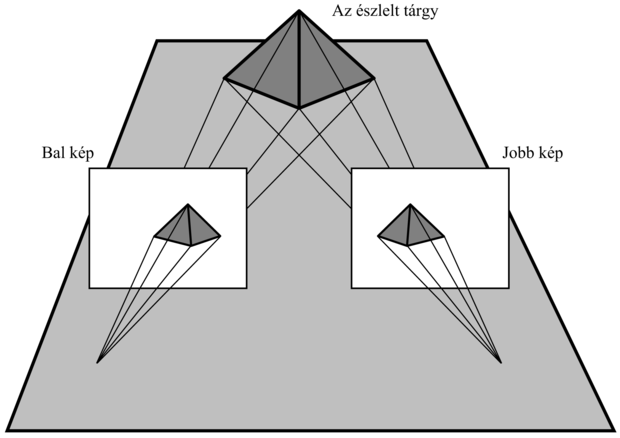
Dolgozzuk ki a diszparitás és a mélység geometriai kapcsolatát. Először azt az esetet vizsgáljuk meg, amikor a két szem (illetve a két kamera) előrenéz, és optikai tengelyük párhuzamos. A jobb és a bal kamera kapcsolata így egy b nagyságú (bázisvonal) transzláció az x koordináta-tengely mentén. A H = v_x ∆t vízszintes és V = v_y∆t függőleges képeltérés számításához az optikai folyam előbb megismert kifejezéseit használhatjuk, T_x = b/∆t, T_y = T_z = 0 mellett. Az ω_x, ω_y, és ω_z rotációs paraméterek zérusok. Azt kapjuk eredményül, hogy H = b/Z és V = 0. Szavakkal megfogalmazva ez azt jelenti, hogy a vízszintes képeltérés a bázisvonal és a mélység aránya, a függőleges eltérés pedig zérus.

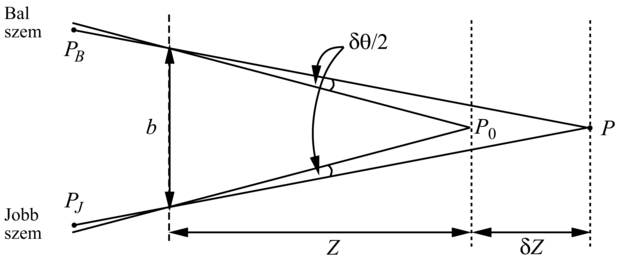
Normális látási körülmények között az emberek fixálnak, azaz összetartóan néznek előre (fixate), vagyis a jelenetben létezik egy olyan pont, amelyben a két optikai tengely metszi egymást. A 24.11. ábra egy P₀ pontra fixáló szemeket mutat, amely pont a két szem középvonalától Z távolságban helyezkedik el. Az egyszerűség kedvéért szögeltérést fogunk számítani radiánban. Az összetartás P₀ pontjában az eltérés zérus. A jelenet egy δZ-vel távolabbi P pontja esetén számíthatjuk a P pont P_L bal és a P_R jobb oldali képének a szögeltolódását. Ha azok mindegyike a P₀ -hoz képest δθ/2 szöggel eltolt, akkor a P_L és a P_R eltolódása, ami a P képeltérése, pontosan δθ. Egyszerű geometriai átalakításokból azt fogjuk kapni, hogy:

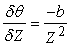
Embereknél a b bázisvonal (baseline) kb. 6 cm. Tegyük fel, hogy Z kb. 100 cm. A legkisebb detektálható δθ (ami a képpont nagyságával függ össze) kb. 5 szögmásodperc, avagy 2,42 × 10^–5 radián, amiből a δZ 0,4 mm-re adódik. Z = 30 cm-re δZ = 0,036 mm-es lenyűgöző értéket kapunk. Ez azt jelenti, hogy 30 cm-es távolságban az emberek akár a 0,036 mm-es képmélység különbség megkülönböztetésére is képesek. Ez teszi lehetővé, hogy be tudjuk fűzni a cérnát egy tűbe, és hasonló műveleteket tudunk elvégezni.

A mindennapi nyelvben a textúra vagy felületmintázat (texture) a felület kitapintható tulajdonságaira vonatkozik (az angol nyelvben ugyanazzal a szótővel rendelkezik, mint maga a szövet^[272]). A számítógépes látásban a textúra egy ehhez közeli fogalomra, egy felületnek a síkban ismétlődő, vizuálisan érzékelhető mintázatára vonatkozik. Példaként említhetjük egy épület ablakainak a mintázatát, egy szvetter kötési mintáját, a leopárd foltos bundáját, a pázsit fűszálainak a mintázatát, kavicsokat a strandon vagy embertömeget egy stadionban. Az elrendezés néha közel periodikus, mint például a kötési szemek a szvetteren, más esetekben, mint például a strandon lévő kavicsok esetén, a szabályosság csak statisztikai értelemben létezik – a kavicsok sűrűsége a strand különböző részein nagyjából azonos.

24.12. ábra - (a) A textúragradienseket illusztráló jelenet. Feltéve, hogy a valós mintázat egyforma, lehetővé teszi a felület irányágának a meghatározását. A számított irányt a képen oly módon elhelyezett fehér kör és nyíl jelzi, mintha a kört a felületre festették volna abban a pontban. (b) Egy ívelt felület alakjának meghatározása a mintázat alapján. (A képeket Jitendra Malik és Ruth Rosenholtz hozzájárulásával közöljük [Malik és Rosenholtz, 1994].)

Amit most a jelenetre vonatkozóan állítottunk, igaz. A képen a textúraelemek vagy texelek (texels) látszólagos nagysága, alakja, távolsága stb. igencsak változik, ahogy ezt a 24.12. ábra mutatja. A csempelapok a jeleneten azonosak. A lapok kivetített nagyságának és alakjának megváltozásában két fő ok játszik szerepet:

Egy kevés matematikai elemzést követően meghatározhatjuk a különböző texeltulajdonságok, mint pl. a terület, a rövidülés és a sűrűség változási mértékének kifejezéseit. Ezek az ún. textúragradiensek (texture gradients) a felület alakjának és a megfigyelőhöz képesti dőlésének és lejtésének a függvényei.

Ahhoz, hogy az alakot a textúrából kinyerhessük, kétlépcsős eljáráshoz kell folyamodnunk: (a) először mérjük a textúragradienseket; (b) majd becsüljük a mért gradienseket okozni látszó felületalakot, azok dőlését és lejtését. A 24.12. ábra mutatja ezen eljárás eredményeit.

Az árnyalást (shading) – a jelenethez tartozó felület különböző részeiről kapott megvilágítás intenzitásváltozását – a jelenet geometriája és a felület-visszaverési tulajdonságai határozzák meg. A számítógépes grafikában a feladat a kép I(x,y) fényességfüggvényének a megadása, ha a jelenet geometriája és a visszaverődési tulajdonságok adottak. A számítógépes látásban azt reméljük, hogy ez a folyamat invertálható, vagyis visszaállíthatjuk a jelenet geometriáját és visszaverődési tulajdonságait, ha az I(x,y) képfényesség adott. A probléma olyan nehéznek bizonyult, hogy a legegyszerűbb esetektől eltekintve e téren nem sikerült eredményeket elérni.

Induljunk ki egy olyan példából, ahol az alakot tényleg visszanyerhetjük az árnyalásból. Tekintsünk egy Lambert-féle felületet, amit egy távoli, pontszerű fényforrás világít meg. Tételezzük fel azt is, hogy a felület messze van a kamerától, így függőleges síkú vetítést fogunk használni a perspektivikus vetítés megközelítésére. A kép fényessége:

I(x, y) = kn(x, y) · s

ahol k egy skálaegyüttható, n a felület normál egységvektora és s a fényforrás irányába mutató egységvektor. Mivel n és s egységvektorok, skalárszorzatuk a kettő közötti szög koszinusza. A felület alakját az n felület menti változása tartalmazza. Tételezzük fel, hogy k és s ismertek. A problémánk most a felület n normálisának a kiszámítása, ha az I(x,y) képfényesség adott.

Az első megjegyzés, amit meg kell tenni, az az, hogy az n meghatározása az adott (x,y) képpontfényesség ismeretében lokálisan alulhatározott. Ki tudjuk ugyan számítani az n és a fényforrás közötti szöget, ez azonban az n-et csak annyiban korlátozza, hogy egy bizonyos, s irányú és θ = cos^–1(I/k) palástszögű kúp felületén helyezkedik el. Hogy továbbléphessünk, jegyezzük meg, hogy képpontról képpontra az n változása nem lehet tetszőleges. Egy sima felület normálisa csak sima módon változhat – amely korlátozást az integrálhatóság (integrability) szakkifejezéssel jelöljük. Ezt a felismerést számos módszerben fel is használják. Egy lehetséges eljárás az n átírása a Z(x,y) mélység Z_x és Z_y parciális deriváltjainak felhasználásával. Ennek eredménye Z egy parciális differenciálegyenlete, amit megfelelő határfeltételek figyelembevételével Z(x,y)-ra nézve meg lehet oldani.

Az eljárás általánosítható. Nem szükséges, hogy a felület Lambert-féle legyen, és az sem, hogy a fényforrás pontszerű legyen. Lényegében ugyanez a módszer használható, ha sikerül a felület R(n) reflektanciatérképét (reflectance map) meghatározni, amely a felületelem fényességét annak n normálisa függvényében fejezi ki.

Az igazi nehézség a kölcsönös visszaverődések kezelése. Egy tipikus belsőtérjelenet esetén, mint például egy irodában lévő tárgyak esetén a felületeket nem csupán a fényforrások világítják meg, hanem a jelenet más felületeitől visszavert fény is, amelyek tényleges másodlagos fényforrásokként szolgálnak. Ezek a kölcsönös megvilágítási hatások igen jelentősek lehetnek. Az ilyen helyzetben a reflektanciatérkép megközelítés teljes mértékben használhatatlan – a kép fényessége nemcsak a normálison múlik, hanem a jelenet különböző felületeinek bonyolult térbeli viszonyain is.

Az ember az árnyalásból képes valamilyen mértékű alakinformáció kinyerésére, így ez a probléma – minden nehézsége ellenére – továbbá is érdekes marad.

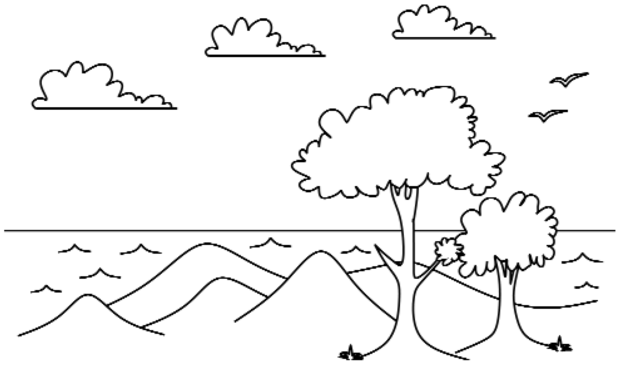
Amikor egy olyan vonalas rajzot nézünk, mint amilyen a 24.13. ábra, a kép egy háromdimenziós elrendezés életszerű benyomását kelti bennünk. Hogyan lehetséges ez? Hiszen láttuk korábban, hogy egy és ugyanaz a vonalas kép végtelen sok jelenet konfigurációból származhat. Figyeljük meg, hogy még a felszín lejtésének és emelkedésének érzetét is megkapjuk. Ez minden bizonnyal (a tipikus alakzatokra vonatkozó) magas szintű tudás és valamilyen alacsony szintű kényszerek összekapcsolásának következtében lehetséges.

24.13. ábra - Egy felidéző vonalas rajz (Isha Malik hozzájárulásával)

A vonalas ábrában rejlő kvalitatív tudással fogunk foglalkozni. Korábban láttuk, hogy a rajz vonalainak különféle lehet a fontossága (lásd 24.4. ábra és kísérőszövege). Az a folyamat, ahogy a kép minden vonalának a tényleges fontosságát megállapítjuk, a vonalcímkézés (line labeling), és ez volt a számítógépes látás által elsőként tanulmányozott problémák egyike. Tegyük fel egyelőre, hogy a világ olyan leegyszerűsített modelljével dolgozunk, ahol a tárgyaknak nincsenek felületei, és ahol az olyan vonalakat, amelyek megvilágítási diszkontinuitásokból adódnak, mint amilyenek az árnyékélek és a tükrözések, valamilyen előfeldolgozó eljárással a képből kiemeltük. A figyelmünket így olyan vonalas ábrákra összpontosíthatjuk, ahol minden vonal vagy mélységi, vagy orientáció diszkontinuitáshoz tartozik.

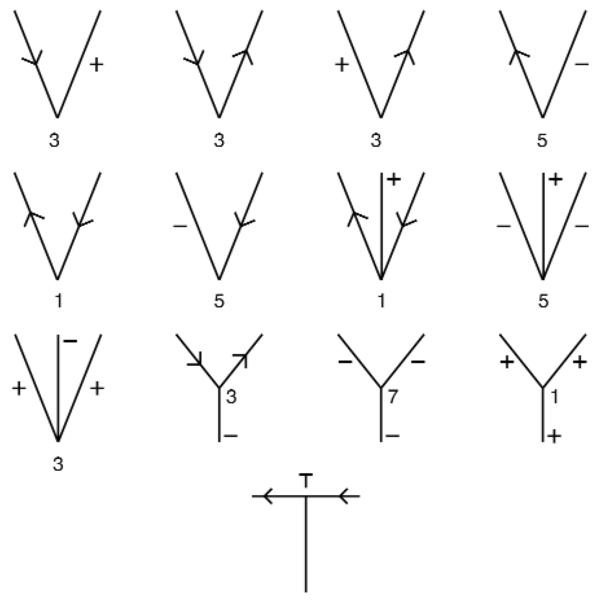
Mindegyik vonalat ezek után vagy egy a felület határán megjelenő pszeudoél (limb) vetületének (ami a felület azon pontjainak összessége, ahol a rálátás iránya a felület érintője), vagy egy élnek (edge) lehet tekinteni (ami a felület normálisának egy diszkontinuitása). Az éleket továbbá konvex, konkáv vagy határoló élosztályokba sorolhatjuk. A pszeudoélek és a határoló élek esetén érdekes annak az eldöntése, hogy a vonalas ábrán a görbét határoló két felületből melyik van hozzánk közelebb. Ezeket a következtetéseket úgy képzelhetjük el, hogy mindegyik vonalhoz a 6 lehetséges vonalcímkének (line label) az egyikét rendeljük hozzá, ahogy az a 24.14. ábrán látható.

24.14. ábra - Különféle vonalcímkék

Egy ábrán található n számú vonal kombinatorikusan elvileg lehetséges címke-hozzárendelésből csupán csekély számú hozzárendelés lehetséges fizikailag. Ezeknek a címkézéseknek a megállapítása az ún. vonalcímkézési probléma. Jegyezzük meg, hogy a probléma csak akkor értelmes, ha a címke a vonal mentén nem változik. Ez nem mindig igaz, hiszen a görbült objektumok képein a címke egy vonal mentén igenis változhat. Ebben a részben ez nem jelent problémát, mert csak poliéderes objektumokkal foglalkozunk.

A poliéderes jelenetelemzéssel először Huffman és tőle függetlenül Clowes próbálkoztak (Huffman, 1971; Clowes, 1971). Huffman és Clowes elemzésüket a nem átlátszó triéderes (trihedral) testekből – azaz olyan testekből, amelyeknél mindegyik sarokpontjánál pontosan három felület fut össze – álló jelenetek esetére korlátozták. A több objektumot tartalmazó jelenetek esetén kizárták a triéderes feltételt megsértő objektumkonfigurációkat is, mint amilyen például az egyik élük mentén érintkező két kocka. Nem engedték a repedéseket (cracks) sem, azaz olyan „éleket”, amelyek mentén a tangenciális síkok folytonosan változnak. A triéderes világban Huffman és Clowes kimerítő listát adtak az összes különböző sarokponttípusról meg arról is, hogy azok hogyan látszhatnak általános nézőpontból szemlélve. Az általános nézőpont feltétel lényegében azt tételezi fel, hogy az összes csatlakozás megtartja a jellegét, ha a szem csak kissé mozdul el. Ha például a képen három vonal metszi egymást, akkor a feltételből következik, hogy a jelenet hozzájuk tartozó éleinek szintén metszeniük kell egymást.

24.15. ábra - A triéderes csúcsok négy fajtája

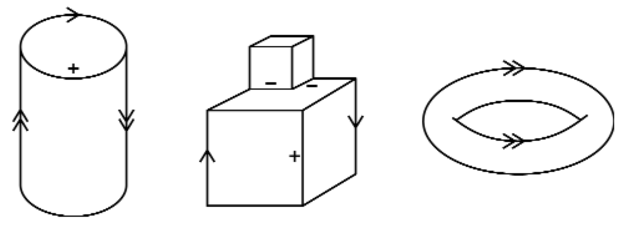
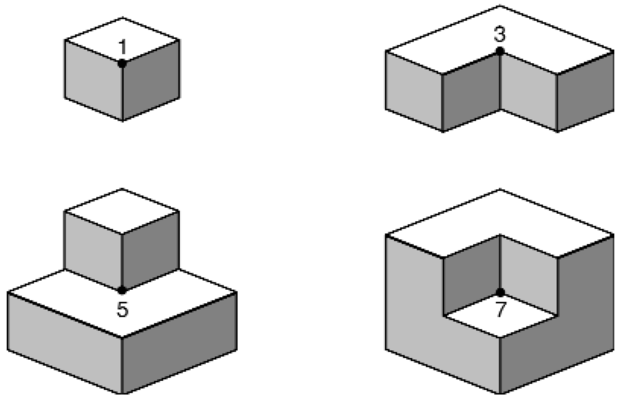
A 24.15. ábra mutatja azt a négyféle helyzetet, ahogy a három síkfelület egy sarokpontban találkozhat. Ezeket az eseteket úgy szerkesztettük, hogy egy kockát nyolc oktánsra (octant) bontottunk. A triéderes sarokpontok egész választékát szeretnénk generálni a kocka középpontjában úgy, hogy a különböző oktánsokat kitöltjük. Az 1-es címkéjű sarokpont az egyetlenegy kitöltött oktánshoz tartozik, a 3-as címkéjű a három kitöltött oktánshoz és így tovább. Az olvasónak kellene belátnia, hogy ezek tényleg kimerítik az összes lehetséges helyzetet. Ha valaki például a kockában két oktánst kitölt, akkor nem lesz képes a középpontban egy érvényes triéderes sarokpontot megszerkeszteni. Jegyezzük meg azt is, hogy ezen négy eset a sarokpontban találkozó konvex és konkáv élek különböző kombinációinak felel meg.

A sarokpontban találkozó három él a körülöttük lévő teret nyolc oktánsra osztja. A sarokpontot bármely, anyaggal nem kitöltött oktánsból lehet szemlélni. A nézőpont oktánson belüli elmozdítása a képen látható csatlakozások jellegét megváltoztatni nem fogja. A 24.15. ábrán látható 1-es címkéjű sarokpontot a maradó hét oktánsból szemlélve a 24.16. ábrán látható csatlakozáscímkéket kapjuk.

Annak kimerítő vizsgálata, hogy egy sarokpont milyen módon látható, a 24.17. ábrán felsorolt lehetőségekhez vezet. A képen négy különböző csatlakozástípust azonosíthatunk: L, Y, nyíl- és T csatlakozást. Az L csatlakozás a két látható él esete. Az Y és a nyílcsatlakozás három élnek felel meg. Az Y csatlakozásban a szögek egyike sem lépi túl a 180°-ot. A T csatlakozás a takarással kapcsolatos. Ha egy közeli, nem átlátszó felület egy távolabbi élt eltakar, egy fél éllel találkozó folytonos élt kapunk. A T csatlakozás négy címkéje a négyféle él takarásának felel meg.

24.16. ábra - A 24.15. ábrán 1-gyel jelölt csúcs különböző előfordulásai

24.17. ábra - A Huffman–Clowes-címkekészlet

Ha egy vonalas rajzot ennek a csatlakozásszótárnak a segítségével címkézünk meg, a probléma annak a megállapítása, hogy mely csatlakozásinterpretációk lesznek globálisan konzisztensek. A konzisztenciát az a szabály kényszeríti ki, miszerint a rajzon egy vonalnak egy és csakis egy címkéje lehet a vonal egész hosszában. Ezen probléma algoritmikus megoldását Waltz adta meg (pontosabban egy olyan kibővített probléma megoldását adta meg, amely az árnyékot, a görbületi diszkontinuitásokat [repedéseket] és a szétválaszthatóan konkáv éleket is figyelembe veszi [Waltz, 1975]). Az algoritmus a kényszerkielégítés egyik legelső alkalmazása volt az MI területén (lásd 5. fejezet). A kényszerkielégítés nyelvén a változók a csatlakozások, a változók értékei a csatlakozások címkézése, a kényszer pedig az, hogy minden vonalnak csak egy címkéje van. Bár a triéderes vonalcímkézési probléma NP-teljes, a közönséges kényszerkielégítési algoritmusok a gyakorlatban jól működnek.