24.3. Előzetes képfeldolgozási műveletek
Láttuk eddig, hogy a fény hogyan tükröződik a jelenet tárgyairól egy mondjuk ötmillió hárombájtos képpontból álló képet formálva. Mint minden érzékelő esetében, most is lesz zaj a képben, és minden esetben nagyon sok adattal kell dolgozni. Elsőként a finomítás műveleteit nézzük meg, amelyekkel a zaj csökkenthető, majd az éldetektálás műveleteit vizsgáljuk. Ezeket „előzetes” vagy „alacsony szintű” műveleteknek hívjuk, mivel ezek az elsők egy műveletsorozatban. Az előzetes látási műveletekre egyrészt a lokalitás jellemző (a kép egy részletére végrehajthatók anélkül, hogy néhány képpontnál messzebb bármit is figyelembe vennénk), másrészt az ismeretek hiánya: anélkül finomíthatjuk a képeket vagy detektálhatunk éleket, hogy bármilyen fogalmunk lenne arról, milyen objektumok vannak a képeken. Ez az alacsony szintű műveleteket esélyessé teszi a párhuzamos hardveren történő megvalósításra, akár élőlényekben, akár mesterséges eszközökben. Ezek után a középső szinten levő műveletek nézzük majd meg, amelyekkel a kép régiókra bontható. A műveletek ezen fázisa még mindig a képen dolgozik, nem a jeleneten, de nem helyi feldolgozást igényel.
A 15.2. alfejezetben a simítás (smoothing) azt jelentette, hogy egy állapotváltozó értékét jósoltuk meg valamilyen múltbeli t időpontra, bizonyos, a t időpontra és további, egészen a jelenig terjedő időpontokra vonatkozó tények ismeretében. Most ugyanezt az ötletet alkalmazzuk a térbeli kiterjedésre az időbeli helyett: a simítás egy képpont értékének jóslását jelenti a környező képpontok alapján. Vegyük észre, hogy világosan megkülönböztetjük a képpontban mért megfigyelt értéket és azt a valódi értéket, amit ott mérnünk kellett volna. Ezek véletlenszerű és szisztematikus mérési hibák (például ha a CCD érzékelője elromlott) miatt különbözhetnek.
A simítás egyik módszere az, ha minden képponthoz az őt környező szomszédok értékeinek átlagát rendeljük. Ez az extrém értékek kihagyása felé mutató megoldás. De hány szomszédot kell figyelembe vennünk – az egy képpontnyi távolságra vagy a kettő esetleg több pont távolságra lévőket? Erre egy válasz, amely jól működik Gauss-zajok kiszűrésére, a Gauss-szűrőt (Gaussian filter) használó súlyozott átlag. Emlékezzünk a standard δ szórással rendelkező Gauss-függvényre:
Egy Gauss-szűrő alkalmazása azt jelenti, hogy az I(x0, y0) intenzitást lecseréljük a minden (x, y)-ra kiszámolt I(x, y)Gσ(d) intenzitások összegével, ahol d az (x0, y0) és az (x, y) pontok távolsága. Az ilyen fajta súlyozott összeg olyan gyakori, hogy van számára egy speciális elnevezés és jelölés. Azt mondjuk, hogy a h függvény az f és a g függvények konvolúciója (convolution) (amit h = f ∗ g alakban írunk), ha
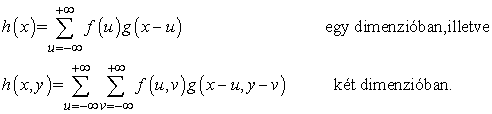
Azaz a simított függvényt úgy kapjuk, hogy a képet a Gauss-függvénnyel konvolváljuk: I ∗ Gσ. Egy képpontnyi σ kevés zaj kisimításához elegendő, míg 2 képpontnyi több zajt fog elsimítani, de valamilyen mértékű részletvesztés mellett. Mivel a Gauss-hatás a távolsággal eltűnik, a gyakorlatban a ± ∞ a szummákban ± 3σ-val helyettesíthető.
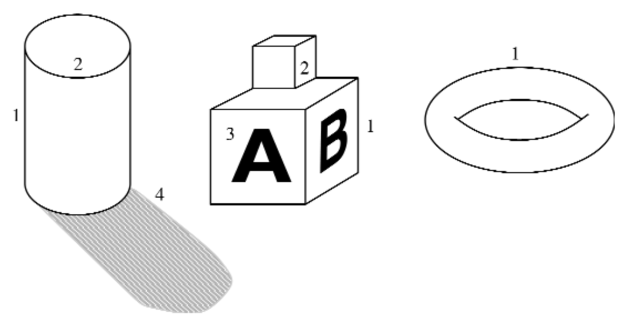
Az előzetes látás következő lépése az élek (edges) detektálása a képsíkon. Az élek olyan egyenes vagy görbe vonalak a képsíkon, amelyekre merőlegesen a kép fényességében „lényegesen” változás van. Az éldetektálás végső célja, hogy eltávolodjunk a bonyolult, több megabájtos képtől egy tömörebb, absztrakt reprezentáció felé, mint amilyen a 24.4. ábrán látható. Az indíték az, hogy a kép élkontúrjai a jelenet fontos kontúrjainak felelnek meg. A képen három mélységi diszkontinuitás példa szerepel 1-gyel címkézve; a 2-vel címkézett felületi orientáció diszkontinuitásból két példa látható, míg a 3-mal címkézett visszaverődési képesség diszkontinuitásokról és a 4-gyel címkézett fényességi diszkontinuitásokról (árnyék) egy-egy. Az éldetektálás csak a képpel foglalkozik, így nem tesz különbséget a jelenet ezen diszkontinuitásfajtái között, de a későbbi feldolgozás igen.
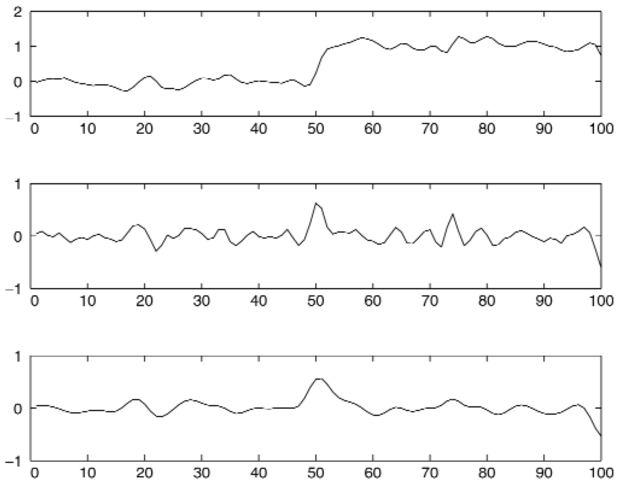
A 24.5. (a) ábra egy asztalon nyugvó tűzőgépet tartalmazó jelenet képét mutatja, a 24.5. (b) pedig a képre lefuttatott éldetektáló algoritmus eredményét mutatja. Láthatjuk, hogy az éldetektáló kimenete és az ideális vonalas ábra között van különbség. A kis részek élei nem mind illeszkednek egymáshoz, vannak hézagok, ahol nincsenek vonalak, valamint „zajos” kontúrok, amelyek a jeleneten semmilyen lényeges vonásnak nem felelnek meg. A későbbi feldolgozási fázisokban ezeket a hibákat majd korrigálni kell. Hogyan detektáljuk a képen az éleket? Figyeljük meg a kép fényintenzitás-profilját egy egydimenziós keresztmetszet mentén egy élre merőleges irányban, pl. az asztal bal éle és a fal között. Nagyjából olyan lesz ez, mint amit a 24.6. (a) ábra mutat. Az él helye az x = 50-nek felel meg.
24.4. ábra - Különféle élek: (1) mélységi diszkontinuitás, (2) felületi orientáció diszkontinuitás, (3) viszszaverődési képesség diszkontinuitás, (4) fényességi diszkontinuitás (árnyékok)
Tekintettel, hogy az élek azoknak a képhelyeknek felelnek meg, ahol a fényességben hirtelen változás tapasztalható, egy naiv ötlet az lehetne, hogy a képet differenciáljuk, és azokat a helyeket keressük meg, ahol az I'(x) derivált értéke nagy. Nos, az ötlet majdnem működőképes. A 24.6. (b) ábrán láthatjuk, hogy az x = 50 csúccsal együtt más helyeken, másodlagos csúcsok is megjelentek (például x = 75), amiket tévesen valódi éleknek fogadhatunk el. A jelenség oka a kép zajossága. Ha a képet először simítjuk, akkor a felesleges csúcsok eltűnnek, ahogy azt a (c) mutatja.
24.6. ábra - Felül: Az I(x) intenzitásprofil egy egydimenziós részlet mentén egy lépcsőfok élén át. Középen: Az intenzitás deriváltja, I'(x). A függvény nagy értékei éleknek felelnek meg, de a függvény zajos. Lent: Az intenzitás simított változatának deriváltja, (I ∗G σ)', amely I ∗ G'-hoz hasonlóan egy lépésben számolható. Az x = 75 pontban levő zajos él jelölt eltűnt.
Van arra esélyünk, hogy optimalizáljuk a munkát ezen a ponton: egyetlen műveletben kombinálhatjuk a simítást és az éldetektálást. Egy tétel szerint tetszőleges f és g függvények esetén megmutatható, hogy a konvolúció deriváltja (f ∗ g)' megegyezik a derivált konvolúciójával: f ∗ (g)'. Tehát ahelyett, hogy először simítanánk, majd differenciálnánk, egyszerűen konvolváljuk a képet a Gauss simító függvény deriváltjával, G'σ-val. Így az egydimenziós éldetektálás algoritmusa a következő:
-
Az I képet a G'σ-val kell konvolválnunk, hogy az R-et megkapjuk.
-
Jelöljük be az azokat a csúcsokat ||R(x)||-ben, amelyek egy előre definiált T küszöbnél magasabbak. A küszöb értékét úgy határozzuk meg, hogy a zaj miatti másodlagos csúcsokat elimináljuk.
Két dimenzióban egy él irányítottsága tetszőleges θ szögű lehet. A függőleges élek detektálásának módja nyilvánvaló: G'σ(x) Gσ(y)-nal kell konvolválnunk a képet. A hatás y irányban simító (a Gauss-konvolúció miatt), x irányban pedig egy simítással kísért differenciálás. A függőleges élek detektálási algoritmusa így az alábbi:
-
Konvolváljuk az I (x, y) képet az fV(x, y) = G'σ (x) Gσ (y)-nal, hogy az RV(x, y) -t megkapjuk.
-
Jelöljük be azokat a csúcsokat az ||RV (x, y)||-ben, amelyek egy előre definiált Tn küszöbnél magasabbak.
A tetszőleges orientációjú él detektálásához a képet két szűrővel: az fV = G'σ(x) Gσ(y) és az fH = G'σ(y) Gσ(x) szűrővel kell konvolválni (az fH az fV 90°-kal elforgatott változata). A tetszőleges orientációjú éldetektáló algoritmus az alábbi:
-
Konvolváljuk az I (x, y) képet az fV (x, y)-nal, valamint az fH (x, y)-nal, hogy az RV(x, y)-t és az RH(x, y) -t megkaphassuk. Definiáljuk az
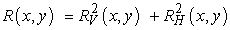-t. -
Jelöljük be azokat a csúcsokat az ||R(x, y)||-ban, amelyek egy előre definiált T küszöbnél magasabbak.
Miután ezzel az algoritmussal megjelöltük az élek képpontjait, a következő lépés az azonos élekhez tartozó képpontok összekötése. Ez megtehető, ha feltételezzük, hogy bármely két szomszédos képpont, amely élpont és konzisztens irányítottságú, szükségszerűen ugyanahhoz az élhez tartozik. Ezt a folyamatot Canny-féle éldetektornak (Canny edge detection) nevezzük, kitalálója, John Canny után.
Miután detektáltuk őket, az élek alkotják több következő feldolgozási lépés alapját: felhasználhatjuk őket a térbeli képalkotásban, a mozgásdetektálásban és az objektumok felismerésében.
Az emberek rendszerezik észleléseiket; az egyes fotóérzékelőkhöz tartozó fényességértékek halmaza helyett vizuális csoportokat észlelünk, amelyek általában objektumokkal vagy azok részeivel asszociáltak. Ez a képesség a számítógépes látás számára is éppúgy fontos.
A szegmentálás (segmentation) a kép felbontása részcsoportokra a képpontok hasonlósága alapján. Az alapötlet a következő: minden képponthoz rendelhetünk bizonyos vizuális tulajdonságokat, mint például fényesség, szín és mintázat.[271] Ezek az attribútumok egy objektumon vagy annak egyetlen részén belül, csak kismértékben változnak, míg az objektumok közötti határok mentén tipikusan egyik vagy másik attribútum jelentősen változik. Úgy kell a képet képpontok halmazaira felosztanunk, hogy ezeket a kényszereket amennyire csak lehet, kielégítsük.
Többféle módszer létezik ezen intuitív elképzelés matematikai formalizálására. Például Shi és Malik (Shi és Malik, 2000) ezt gráfparticionálási problémaként határozzák meg. A gráf csomópontjai a képpontoknak felelnek meg, az élek pedig a köztük levő kapcsolatoknak. Egy Wij súly értéke az i és j képpontokat összekötő élen attól függ, hogy a két képpont mennyire hasonló fényességben, színben, mintázatban és más tulajdonságokban. Ezek után olyan partíciókat keresnek, amelyek minimalizálnak egy normalizált vágási kritériumot. Durván fogalmazva a gráf particionálásának kritériuma, hogy a csoportok közötti élek súlyainak összegét minimalizáljuk, a csoportokon belüli élek súlyainak összegét pedig maximalizáljuk.
A pusztán alacsony szintű, helyi tulajdonságokon – például a fényességen és színen – alapuló szegmentáció hibázásra hajlamos eljárás. Ahhoz, hogy az objektumokhoz rendelt határokat megbízhatóan megtalálhassuk, a jelenetben várható objektumfajtákról magas szintű tudást is be kell építenünk. A beszédfelismerésre ezt a rejtett Markov-modell formalizmusa teszi lehetővé, míg a képek kontextusában egy ilyen egységes keretrendszer még mindig az aktív kutatás tárgya. Mindenesetre az objektumokról szóló magas szintű tudás a következő alfejezet tárgya.
[271] A mintázati jellemzők a képpontra középpontozott kis felületdarabka statisztikai elemzésén alapulnak.
