23.1. Valószínűségi nyelvi modellek
A 22. fejezet a nyelv logikai modelljét adta meg: CFG-ket és DCG-ket használtunk, hogy egy adott karakterfüzérről eldöntsük, eleme-e vagy sem egy nyelvnek. Ebben az alfejezetben számos valószínűségi modellt vezetünk be. A valószínűségi modellek számos előnnyel rendelkeznek. Kényelmesen taníthatók adatok alapján: a tanulás mindössze az előfordulások megszámlálásából áll (némi tűréssel a kis mintaméret okozta hibák miatt). Továbbá robusztusabbak (mivel bármely karakterfüzért elfogadnak, habár kis valószínűséggel), visszatükrözik azt a tényt, miszerint nem a beszélők 100%-a ért egyet abban, hogy mely mondatok részei a nyelvnek; valamint alkalmasak a többértelműség feloldására: a valószínűségre támaszkodva kiválasztható a legvalószínűbb értelmezés.
A valószínűségi nyelvi modell (probabilistic language model) valószínűségi eloszlást definiál egy (esetleg végtelen) karakterfüzér-halmaz felett. Példaként állhatnak a 15.6. alfejezetben beszédmegértésre használt bi- és trigram nyelvi modellek. Az unigram modell P(w) valószínűséget rendel a szókincs minden egyes szavához. A modell feltételezi, hogy a szavak függetlenül lettek kiválasztva, azaz a karakterfüzér valószínűsége egyszerűen a szavak valószínűségének szorzata: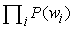
. A következő húszszavas szekvenciát véletlen módon generáltuk, a könyv szavainak unigram modellje alapján:[236]
logical are as confusing a may right tries agent goal the was diesel more object then information-gathering search is
A bigram modell egy P(wi|wi–1) valószínűséget rendel minden egyes szóhoz, adott előző szó esetén. A 15.21. ábra néhány bigram-valószínűséget mutatott be. A könyv bigram modellje a következő véletlen szekvenciát generálja:
planning purely diagnostic expert system are very similar computational approach would be represented compactly using tic tac toe a predicate
Általánosan, egy n-gram modell az előző n – 1 szó alapján szabja meg a P(wi|wi–(n–1)…wi–1) valószínűséget. A könyv trigram modellje ezt a véletlen szekvenciát generálja:
planning and scheduling are integrated the success of naive bayes model is just a possible prior source by the time
Még a fenti kis példa alapján is láthatónak kell lennie, hogy a trigram modell jobb, mint a bigram (amely pedig jobb, mint az unigram), mind az angol nyelv, mind egy MI-tankönyv témájának közelítésében. A modellek maguk is egyetértenek ezzel: a trigram modell a véletlen módon generált sztringjéhez 10–10 valószínűséget rendel, a bigram 10–29-et, az unigram pedig 10–59-et.
Ez a könyv félmillió szavával nem tartalmaz elég adatot ahhoz, hogy jó minőségű bigram modellt lehessen előállítani belőle, nem is beszélve a trigram modellről. A könyv szókincse körülbelül 15 ezer különböző szót tartalmaz, tehát a bigram modell 15 0002 = 225 millió szópárt tartalmaz. Világos, hogy a szópárok legalább 99,8%-a 0 gyakoriságú, de nem akarjuk, hogy a modell azt állítsa, hogy ezek a szópárok lehetetlenek. Szükségünk van valamilyen simításra (smoothing) a nulla gyakoriságok felett. A legegyszerűbb megoldás az adj-hozzá-egyet simítás (add-one smoothing): minden lehetséges bigram gyakoriságához hozzáadunk egyet. Azaz amennyiben a korpuszban N szó és B lehetséges bigram található, akkor minden c gyakoriságú bigramhoz egy (c + 1)/(N + B) értékű valószínűség-becslőt rendelünk. Ez a módszer megszünteti a nulla valószínűségű n-gramok problémáját, de az a követelmény, hogy minden gyakoriságot pontosan eggyel kell növelni, kétséges, és rossz becslésekhez vezethet.
A másik megközelítés a lineáris interpoláción alapuló simítás (linear interpolation smoothing), ami lineárisan kombinálja a trigam, bigram és unigram modelleket. A valószínűség-becslőt a következőképpen definiáljuk:
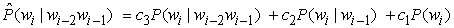
ahol c3 + c2 + c1 = 1. A ci paraméterek lehetnek rögzítettek vagy EM algoritmussal taníthatók. Az is lehetséges, hogy a ci értékeket az n-gram gyakoriságoktól függőnek választjuk, azaz nagyobb súlyt adunk azoknak a valószínűségi becslőknek, amelyeket nagyobb gyakoriságokból számítunk.
A nyelvi modell egyik lehetséges kiértékelési módja a következő: először válasszuk szét a korpuszt egy tanító és egy teszthalmazra. Határozzuk meg a modell paramétereit a tanító halmaz alapján. Ezután számítsuk ki a valószínűséget a teszthalmazra a modell alapján; minél nagyobb a valószínűség, annál jobb. A megközelítés egyik problémája az, hogy hosszú karakterfüzérek esetén a P(szavak) nagyon kicsi; a kis számok lebegőpontos alulcsordulást okozhatnak, vagy egyszerűen túl nehéz lenne elolvasni őket. Tehát a valószínűség helyett a modell összetettségét (perplexity) számíthatjuk ki a teszt karakterfüzéren:
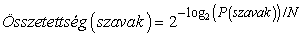
ahol N a szavak száma. Minél kisebb az összetettség, annál jobb a modell. Az az n-gram modell, amely minden szóhoz 1/k valószínűséget rendel, k összetettségű; az összetettséget úgy is lehet értelmezni, mint átlagos elágazási tényezőt.
Példaként arra, hogy mire képesek az n-gram modellek, vegyük a szegmentáció (segmentation) feladatát, ami szóhatárok megtalálása szóköz nélküli szövegben. Ez a feladat elengedhetetlen a japán és kínai nyelv esetén; ezek olyan nyelvek, amelyek nem raknak szóközt a szavak közé, feltételezzük azonban, hogy a legtöbb olvasónak az angol nyelv[237] jobban megfelel. Az
Itiseasytoreadwordswithoutspaces[238]
mondatatot tényleg könnyű elolvasni. Az olvasó arra gondolhat, hogy ezt az teszi lehetővé, hogy teljesen ismerjük az angol szintaktikát, szemantikát és pragmatikát. Meg fogjuk mutatni, hogy a mondatot egy egyszerű unigram modellel is könnyen dekódolni lehet.
Korábban láthattuk, hogy a Viterbi algoritmus (15.9) hogyan használható a legvalószínűbb szekvencia megtalálására egy szó-valószínűségi hálóban. A 23.1. ábrán látható a Viterbi algoritmus olyan változata, amelyet specifikusan a szegmentációs probléma megoldására terveztünk. Bemenete a P(szó) unigram valószínűségi eloszlás és egy karakterfüzér. Ezután az algoritmus a karakterfüzér minden egyes i pozíciójára a legjobb[i] elemben eltárolja a legvalószínűbb i-ig tartó karakterfüzér valószínűségét. Emellett a szavak[i] elemben eltárolja azt az i-edik pozícióban végződő szót, ami a legnagyobb valószínűséget adta. Miután felépítette a legjobb és a szavak tömböket dinamikus programozási módon, hátrafelé mozogva feldolgozza a szavak tömböt, hogy megtalálja a legjobb utat. Ebben az esetben, a könyv unigram modellje alapján a legjobb szekvencia ténylegesen az „It is easy to read words without spaces”,[239] 10–25 valószínűséggel. A szekvencia részeinek összehasonlítása során látható, hogy az „easy” unigram valószínűsége 2,6 × 10–4, miközben az alternatív „e as y”[240] valószínűsége sokkal kisebb, 9,8 × 10–12 annak ellenére, hogy a könyv képleteiben viszonylag gyakran előfordul az „e” és az „y”. Hasonlóképpen:
P(„without”) = 0,0004
P(„with”) = 0,005; P(„out”) = 0,0008
P(„with out”) = 0,005 × 0,0008 = 0,000004
Ennek következtében az unigram modell szerint a „without” százszor nagyobb valószínűségű, mint a „with out”.[241]
23.1. ábra - Viterbi-alapú szószegmentáló algoritmus. Egy szóközöket nem tartalmazó szófüzért feldolgozva megadja a legvalószínűbb szavakra történő szegmentációt.
Ebben a bekezdésben a szavak feletti n-gram modellekről értekeztünk, azonban az n-gram modelleket számos egyéb egység – például karakterek vagy beszédrészek (parts of speech) – felett is lehet értelmezni.
Az n-gram modellek a korpuszon belüli közös előfordulási statisztikát használják ki, azonban nincs semmilyen információjuk a nyelvtanról n-nél nagyobb távolságra. A valószínűségi környezetfüggetlen nyelvtan – PCFG[242] (probabilistic context-free grammar) – egy alternatív nyelvi modell, ami egy olyan CFG, melyben minden átírási szabályhoz valószínűséget rendelünk. Az azonos bal oldallal rendelkező szabályok valószínűségének összege 1. A 23.2. ábrán az ℰ0 nyelvtan egy részletének PCFG-je látható.
23.2. ábra - Az ℰ0 nyelvtan egy részletének valószínűségi környezetfüggetlen nyelvtana (PCFG) és szókincse. A szögletes zárójelben levő szám jelzi a valószínűségét annak, hogy az adott bal oldali szimbólumot a megfelelő szabály szerint írjuk át
23.3. ábra - A „Minden wumpus bűzlik” mondat elemzési fája, megadva minden egyes részfa valószínűségét. A teljes fa valószínűsége 1,0 × 0,5 × 0,05 × 0,15 × 0,60 × 0,10 = 0,000225. Mivel a mondatnak ez az egyetlen elemzése, ezért ennyi a mondat valószínűsége is.
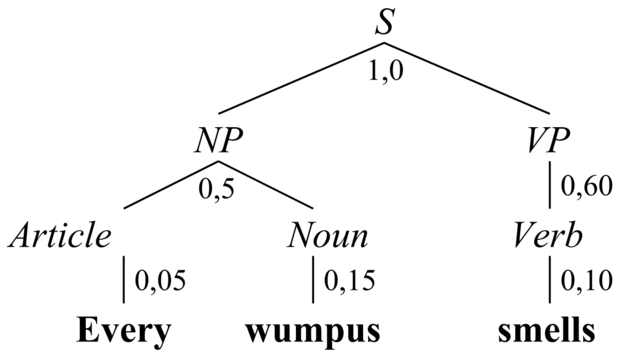
A PCFG-modellben egy karakterfüzér valószínűsége – a P(szavak) – egyszerűen az elemzési fái valószínűségeinek összege. Egy adott fa valószínűsége a fa csomópontjait felépítő szabályok valószínűségeinek szorzata. A 23.3. ábra bemutatja, hogyan lehet kiszámítani egy mondat valószínűségét. A valószínűség kiszámítható egy CFG diagramelemző alkalmazásával, amely megadja az összes lehetséges elemzést, majd egyszerűen össze kell adni a valószínűségeket. Azonban ha csak a legvalószínűbb elemzés érdekel minket, akkor a nem valószínű elemzések meghatározása pazarlás. A legvalószínűbb elemzés hatékony megtalálására használhatunk egy Viterbi algoritmus variációt vagy egy legjobbat-először keresési technikát (mint például az A*-ot).
A PCFG-vel az a probléma, hogy környezetfüggetlen. Ez azt jelenti, hogy a különbség a P(„eat a banana”) és a P(„eat a bandanna”)[243] között mindössze a P(„banana”) és P(„bandanna”) közti különbségtől függ, és nem az „enni” ige és a megfelelő objektumok közti kapcsolattól. Hogy megkapjuk ezt a kapcsolatot, szükség van valamilyen környezetfüggő modellre, mint például a szókinccsel ellátott PCFG-re (lexicalized PCFG), amelyben a kifejezés feje[244] szerepet játszhat a kifejezés valószínűségének meghatározásában. Elegendő tanító adat esetén a VP → VP NP szabály kondicionálható a beágyazott VP fejére („enni”) és az NP fejére („banán”). Ezáltal a szókinccsel ellátott PCFG-k képesek az n-gram modellek közös előfordulási megszorításai egy részének a megragadására, megtartva a CFG-modellek nyelvtani megszorításait.
A PCFG másik problémája az, hogy erősen preferálja a rövid mondatokat. Egy olyan korpuszban, mint a Wall Street Journal, az átlagos mondathossz körülbelül 25 szó. Azonban egy PCFG általában úgy végez, hogy viszonylag magas valószínűséget rendel olyan szabályokhoz, mint az S → NP VP, az NP → Pronoun és a VP → Verb. Ez azt jelenti, hogy a PCFG viszonylag nagy valószínűséget fog rendelni sok rövid mondathoz, mint pl. „ő aludt”, azonban a Journalban sokkal valószínűbben találkozunk olyan mondatokkal, mint „Egy megbízható kormányzati forrás jelentése szerint az az állítás, hogy aludt, hihető”. Úgy tűnik, hogy a Journal mondatai igazából nem környezetfüggetlenek, hanem az íróknak van elképzelésük az elvárt mondathosszról, amit fel is használnak lágy globális kényszerként a mondatok írásakor. Ezt nehéz visszatükrözni egy PCFG-ben.
Egy PCFG-modell létrehozásához a CFG konstrukciójának összes nehézségével szembesülünk, ehhez hozzátevődik még az egyes szabályok valószínűséggel való ellátása. Ez azt sugallja, hogy a nyelvtan adatokból való tanulása (learning) hasznosabb lehet, mint a tudásmérnöki megközelítés. Csakúgy, mint a beszédmegértés esetén is, kétféle adat áll rendelkezésre: elemzett és nem elemzett. A feladat sokkal egyszerűbb, ha az adatok elemzési fáját nyelvészek (vagy legalábbis képzett anyanyelvi beszélők) készítették el. Egy ilyen korpusz elkészítése óriási feladat, a legnagyobb korpuszok „mindössze” körülbelül egymillió szót tartalmaznak. Az elemzési fa korpusz alapján a PCFG-t egyszerűen számlálással (és simítással) készítjük el: minden egyes nem záró szimbólumra megnézzük az összes olyan csomópontot, amelynek ez a szimbólum a gyökere, és előállítjuk a csomópontok gyermekeinek összes különböző kombinációit leíró szabályokat. Például ha az NP szimbólum 100 000-szer fordul elő, és ebből 20 000 esetben a gyermekek listája [NP, PP], akkor a következő szabályt állítjuk elő:
NP → NP PP [0,20]
A feladat sokkal nehezebb, ha csak elemzetlen szöveggel rendelkezünk. Először is két problémával szembesülünk: a nyelvtani szabályok struktúrájának és az egyes szabályok valószínűségének megtanulásával. (Ugyanezt a megkülönböztetést tesszük neurális hálózatok, valamint Bayes-hálók tanulása esetén is.)
Pillanatnyilag feltételezzük, hogy a szabályok struktúrája adott, és csak a valószínűségeket próbáljuk megtanulni. Alkalmazhatunk egy várhatóérték-maximalizálás (expectation– maximization, EM) módszert, úgy, mint az RMM-ek tanulásánál. A paraméterek – amelyeket tanulni próbálunk – a szabály-valószínűségek. A rejtett változók az elemzési fák: nem tudjuk, hogy a wi…wj szavakból álló karakterfüzért ténylegesen az X → α szabály generálja-e, vagy sem. Az E lépés megbecsüli az egyes részszekvenciák egyes szabályok által történő generálásának valószínűségét. Ezután az M lépés megbecsüli az egyes szabályok valószínűségét. Az egész számítást el lehet végezni dinamikus programozási módon, az ún. belső–külső (inside–outside) algoritmussal, ami a HMM tanulás előre–hátra algoritmusának analógiája.
A belső–külső algoritmus varázslatosnak tűnik, hiszen elemzetlen szövegekből állít elő nyelvtant. Azonban számos hátránnyal rendelkezik. Először is lassú: ahol n a mondatbeli szavak, t pedig a nem záró szimbólumok száma. Másodsorban, a valószínűségi hozzárendelések tere nagyon nagy, és a tapasztalatok alapján a lokális maximumokban való bennragadás súlyos probléma. Alternatív módszerek – például szimulált lehűtés – megpróbálhatók ugyan, de ezek még nagyobb számításigényűek. Harmadsorban, a kapott nyelvtanok által elvégzett elemzések gyakran nehezen érthetők, és nem elégítik ki a nyelvészeket. Ez megnehezíti a manuálisan előállított tudás kombinálását az automatikus indukcióval.
Most pedig tételezzük fel, hogy a nyelvtani szabályok struktúrája nem ismert. Az első probléma, amivel szembesülünk, az, hogy a lehetséges szabályhalmazok tere végtelen, azaz nem tudjuk, hogy hány szabályt vegyünk figyelembe, és azt sem, hogy az egyes szabályok milyen hosszúak lehetnek. A probléma egyik lehetséges megkerülése az, hogy a nyelvtani szabályokat Chomsky normál alakban (Chomsky normal form) tanuljuk, ami azt jelenti, hogy minden szabály a következő két alak egyike lehet:
X → Y Z
X → t
ahol X, Y és Z nem záró, míg t záró szimbólum. Minden környezetfüggetlen nyelvtant át lehet írni Chomsky normál alakra, amely pontosan ugyanazt a nyelvet fogadja el. Ezután önhatalmúlag n nem záró szimbólumra szorítkozhatunk, ezáltal n3 + nv szabályt kapunk, ahol v a záró szimbólumok száma. A gyakorlatban ez a módszer csak kis nyelvtanok esetén bizonyult hatékonynak. A bayesi modellösszevonás (Bayesian model merging) alternatív megközelítés hasonló a SEQUITUR modellhez (lásd 22.8. alfejezet). A módszer mondatonkénti lokális modellek (nyelvtanok) építésével kezd, majd a minimális leíróhossz felhasználásával összevonja a modelleket.
[236] Mivel nem lett volna értelme lefordítani magyarra az egyes szavakat, ezért meghagytuk az eredeti angol nyelvű példát. (A ford.)
[237] Mivel nem lehetett volna hasonló magyar példát valószínűségekkel együtt elkészíteni, ezért meghagytuk az eredeti angol nyelvű példát. (A ford.)
[238] Könnyűszavakatszóközöknélkülolvasni (A ford.)
[239] Könnyű szavakat szóközök nélkül olvasni (A ford.)
[240] easy – könnyű; as – mint (A ford.)
[241] without – nélkül; with – vele; out – kint (A ford.)
[242] A PCFG-k másik megnevezése a sztochasztikus környezetfüggetlen nyelvtan (stochastic context-free grammar), avagy SCFG.
[243] „egy banánt eszik” – „egy selyemkendőt eszik” (A ford.)
[244] A kifejezés feje a legfontosabb szó, például a főnév a főnévi szerkezetben.
