Az ebben a fejezetben használt alapvető koncepciók ismét az adat (data) és a hipotézis (hypothesis), éppúgy, mint ahogy a 18. fejezetben volt. Itt az adatok a tények (evidence) – ezek a területet leíró valószínűségi változók egy részének vagy mindegyikének egy konkrét megvalósulását jelentik. A hipotézis valamilyen valószínűségi elmélet arról, hogy a világ adott területe hogyan is működik, ennek speciális esetei a logikai elmélettel leírt területek.

Vegyünk egy nagyon egyszerű példát. Kedvenc „meglepetés” cukorkánk kétféle, meggy- (nyam-nyam) és citrom- (brrrr) ízben kapható. A cukorkagyártónak sajátos humora van, és mindegyik cukorkát – ízétől függetlenül – ugyanolyan átlátszatlan papírba csomagolja. Az édességet nagyon nagy zsákokban árulják, amelyekből ötféle van – kívülről megint csak megkülönböztethetetlenek egymástól:

h1: 100% meggy

h2: 75% meggy + 25% citrom

h3: 50% meggy + 50% citrom

h4: 25% meggy + 75% citrom

h5: 100% citrom

Egy adott új zsák cukorka esetén a H (hipotézist jelölő) véletlen változó a zsák típusát jelenti, lehetséges értékei h₁-től h₅-ig terjednek. Természetesen H közvetlenül nem figyelhető meg. Ahogy a cukorkákat felbontjuk és megvizsgáljuk, adatokat gyűjtünk – amelyeket D₁, D₂, …, D_N jelöl. Mindegyik D_i egy olyan véletlen változó, amelynek lehetséges értékei a meggy, illetve a citrom. Az ágens feladata, hogy jóslást adjon a következő cukorka ízére.^[194] Ez a nyilvánvalóan triviális feladat érdekes módon mégis jó betekintést nyújt a legfontosabb problémák közül többre is. Az ágensnek valóban elméletet kell alkotnia a világról, bár csak nagyon egyszerűt.

A Bayes-tanulás (Bayesian learning) során egyszerűen kiszámítjuk minden egyes hipotézis valószínűségét az adatokra támaszkodva, majd ennek alapján adunk predikciót. Azaz nem egyetlen „legjobb” hipotézist használunk a predikcióhoz, hanem az öszszes hipotézist használjuk, valószínűségükkel súlyozva őket. Reprezentálja D az összes adatot, legyen d a megfigyelt értékek vektora, ekkor az egyes hipotézisek valószínűségét a Bayes-szabállyal adhatjuk meg:

P(hi|d) = αP(d|hi)P(hi) (20.1)

Tegyük fel, hogy egy ismeretlen X mennyiségre vonatkozó predikció a célunk. Ebben az esetben:

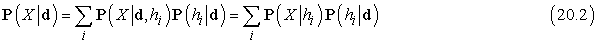
ahol azt feltételeztük, hogy az összes hipotézis meghatároz X-re valamilyen eloszlást. Ez az összefüggés azt mutatja, hogy a predikció az egyes hipotézisekből adódó predikciók súlyozott összege. Maguk a hipotézisek tulajdonképpen a nyers adatok és a predikciók közti „közvetítők”. A Bayes-megközelítésben a P(h_i) prior hipotézisek (hypothesis prior), illetve a hipotézisek mellett fellépő P(d|h_i) adatvalószínűségek (likelihood) a kulcsmennyiségek.

A cukorka példánkban azt feltételezzük, hogy a h₁,…, h₅ a priori valószínűségei megfelelnek a gyártó reklámjában közölt 〈0,1, 0,2, 0,4, 0,2, 0,1〉 értékeknek. Az adatok valószínűségét e.f.e (angol rövidítése: i.i.d.) feltételezéssel számítjuk – azaz egyforma és független eloszlást (independently and identically distributed) teszünk fel, így:

Tegyük fel például, hogy a cukorkás zsák valójában csupa citromtípusú (h₅), és az első 10 kibontott cukorka mind citromízű, ekkor P(d|h₃) = 0,5¹⁰, mivel a h₃ típusú zsákokban a cukorkák fele citrom.^[195] A 20.1. (a) ábra mutatja, hogyan változik az öt hipotézis a posteriori valószínűsége, ahogy sorban észleljük a 10 citromízű cukorkát. Vegyük észre, hogy a valószínűségek az a priori értékekről indulnak, ennek megfelelően kezdetben h₃ a legvalószínűbb lehetőség, és ez így is marad még az első cukor felbontása után is. A második citromízű cukorka felbontása után h₄ a legvalószínűbb, 3 és több esetén h₅ (a rettegett csupa citrom zsák). 10 citromízű cukorka után már meglehetősen biztosak vagyunk végzetünket illetően. A 20.1. (b) ábra mutatja annak a (20.2) egyenlet alapján jósolt valószínűségét, hogy a következő cukorka citromízű. Várakozásunknak megfelelően monoton növekszik az 1 felé.

20.1. ábra - (a) A (20.1) egyenletből számított P(h_i|d₁,…,d_N) a posteriori valószínűségek. A megfigyelések száma 1-től 10-ig terjed, és mindegyik megfigyelés citromízű cukorka. (b) A (20.2) egyenlet alapján számított P(d_N+1 = citrom|d₁,…,d_N) Bayes-predikció.

A Bayes-tanulás optimalitásának természetesen ára van. Mint a 18. fejezetben láttuk, a valós tanulási problémáknál a hipotézistér rendszerint nagyon nagy vagy végtelen. Néha a (20.2) egyenletben az összegzés (vagy folytonos esetben az integrálás) pontos elvégzése kezelhető problémára vezet, de a legtöbb esetben közelítő vagy egyszerűsített megoldásokra kell szorítkoznunk.

Nagyon elterjedt approximációs módszer – a tudományos feladatokban rendszerint ezt alkalmazzuk –, hogy egyetlen, a legvalószínűbb hipotézis alapján végezzük a predikciót, azaz olyan h_i alapján, amely maximálja a P(h_i|d)-t. Ezt maximum a posteriori vagy MAP hipotézisnek nevezzük. A MAP hipotézis alapján végzett predikciók közelítőleg Bayes-predikciók. Ez a közelítés annyira jó, amennyire jó a P(X|d) ≈ P(X|h_MAP közelítés. A cukorka példánkban három egymás utáni citromízű cukor észlelése után h_MAP = h₅, így a MAP-tanulás alapján a negyedik cukorra 1,0 valószínűséggel citromízűt jósolunk. Ez nyilván sokkal veszélyesebb jóslat, mint a Bayes-predikció, amely 0,8valószínűségű, ahogy a 20.1. ábrán is láthatjuk. Ahogy egyre több adatunk van, a MAP és Bayes-predikciók egyre inkább konvergálnak egymáshoz, mivel a MAP hipotézis alternatívái egyre kevésbé valószínűvé válnak. Bár példánk ezt nem mutatja, de a MAP hipotézis előállítása sokszor lényegesen egyszerűbb, mint a Bayes-tanulásé. Ennek oka, hogy csupán egy optimalizálási probléma megoldását igényli, szemben egy nagyon nagy összegzési (vagy integrálási) problémával. A fejezet későbbi részében majd látunk példákat erre.

Mind a Bayes-tanulásban, mind a MAP-tanulásban a P(h_i) a priori hipotézis valószínűségek nagy szerepet játszanak. Láttuk a 18. fejezetben, hogy túlilleszkedés (overfitting) léphet fel, ha túlzottan nagy a hipotézistér kifejezőképessége, vagyis túl sok olyan hipotézist tartalmaz, amely jól illeszkedik az adatokra. A Bayes- és a MAP-tanulás nem alkalmaz valamilyen önkényes korlátot a figyelembe vett hipotézisekre, inkább az a priori valószínűségeket használják fel arra, hogy büntessék a hipotézisek komplexitását. A komplex hipotéziseknek tipikusan kisebb az a priori valószínűsége – részben azért, mert sokkal több komplex hipotézis van, mint egyszerű. Másrészről a komplex hipotéziseknek nagyobb kapacitása van az adatokra való illeszkedéshez. (Extrém esetet véve egy táblázat 1,0 valószínűséggel és tökéletes pontossággal reprodukálni tudja az adatokat.) Ennek megfelelően az a priori valószínűségben testesül meg a hipotéziskomplexitás és az adatokra való illeszkedési képesség közötti kompromisszum.

A hipotéziskomplexitás és az adatokra való illeszkedési képesség közötti kompromisszumot új módon világítja meg, ha a (20.1) egyenlet logaritmusát képezzük. A h_MAP hipotézis olyan kiválasztása, amely maximálja a P(d|h_i)P(h_i)-t ugyanaz, mint amikor minimalizáljuk a következő kifejezést:

–log2P(d|hi) –log2P(hi)

Használjuk fel az információkódolás és a valószínűség között a 18. fejezetben bevezetett kapcsolatot. Azt látjuk, hogy a –log₂P(h_i) tag nem más, mint a h_i hipotézis specifikálásához szükséges bitek száma. A –log₂ P(d|h_i)-tag viszont azoknak a további biteknek a száma, amelyek ahhoz szükségesek, hogy az adott hipotézis feltételezésével specifikáljuk az adatokat. (Ennek demonstrálására mutatjuk be azt az esetet, amikor a hipotézis pontosan megjósolja az adatokat, ilyenkor nincs szükség egyetlen bitre sem az adatok specifikálásához. Ilyen például a h₅ hipotézis esete, amikor sorban érkeznek a citromízű cukorkák – és valóban log₂ 1 = 0.) Ebben az értelemben a MAP-tanulás jellemzője, hogy maximálisan tömöríti az adatokat. Ezt a feladatot sokkal közvetlenebbül célozza a minimális hosszúságú leírás (MHL) (minimum description length, MDL) tanulási módszer, amely a valószínűségekkel való foglalkozás helyett a hipotézis méretének és az adat kódolásának minimalizálására törekszik.

Az utolsó egyszerűsítést az adja, ha a hipotézistérben egyenletes (uniform) priort feltételezünk. Ebben az esetben a MAP-tanulás egy olyan h_i választására redukálódik, amely maximálja P(d|h_i) -t. Ezt maximum-likelihood (ML) hipotézisnek nevezzük, és h_ML-lel jelöljük. A maximum-likelihood tanulás nagyon elterjedt a statisztikában. Ez egy olyan tudomány, amelynek sok kutatója nem bízik az a priori hipotézisek szubjektív természetében. Ez józan megközelítés akkor, amikor nincs semmi okunk, hogy apriori kitüntessük az egyik hipotézist egy másikkal szemben, például amikor az öszszes hipotézis egyformán komplex. Az ML-tanulás jó közelítését adja a Bayes- és MAP-tanulásnak olyankor, amikor az adathalmaz nagy, hiszen az adatok végül is felülírják a hipotézisek a priori eloszlását, de kis adathalmazok esetén problémák merülnek fel az alkalmazásánál (mint látni fogjuk).