17.3. Eljárásmód-iteráció
Az előző alfejezetben megfigyeltük, hogy optimális eljárásmódot akkor is kaphatunk, amikor a hasznosságfüggvény becslése pontatlan. Ha egy cselekvés egyértelműen jobb, mint a többi, akkor a releváns állapotok hasznosságainak a pontos nagyságát nem szükséges precízen tudnunk. Ez a megérzés egy alternatív módot javasol az optimális eljárásmód megkeresésére. Az eljárásmód-iterációs (policy iteration) algoritmus egy π0 kezdeti eljárásmódtól indulva a következő két lépést váltogatja:
-
Eljárásmód-értékelés (policy evaluation): Egy adott πi eljárásmódnál számítsuk ki
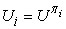 -t, az egyes állapotok hasznosságát mintha πi volna végrehajtva.
-t, az egyes állapotok hasznosságát mintha πi volna végrehajtva. -
Eljárásmód-javítás (policy improvement): Számítsunk ki egy új πi+1 MVH-eljárásmódot, felhasználva az Ui-n alapuló egylépéses előrenézést (mint a (17.4) egyenletben).
Az algoritmus leáll, amikor az eljárásmód-javítás lépése nem eredményez változást a hasznosságokban. Ennél a pontnál tudjuk, hogy az Ui hasznosságfüggvény a Bellman-frissítés egy fix pontja, így a Bellman-egyenletek egy megoldása, és πi-nek egy optimális eljárásmódnak kell lennie. Mivel csak véges sok eljárásmód létezik a véges állapottérben, és megmutatható, hogy minden iteráció jobb eljárásmódot eredményez, az eljárásmód-iterációnak le kell állnia. Az algoritmus a 17.7. ábrán látható.
Az eljárásmód-javítás lépése nyilvánvalóan egyértelmű, de hogyan valósítsuk meg az eljárásmód-értékelést. Kiderül, hogy ennek elvégzése sokkal egyszerűbb, mint a szabványos Bellman-egyenletek megoldása (amit az értékiteráció végez el), mivel az eljárásmód egy cselekvést minden állapotban rögzít. Az i-edik iterációban a πi eljárásmód a πi(s) cselekvést írja elő. Ez azt jelenti, hogy a (17.5) Bellman-egyenlet egy egyszerűsített változatával állunk szemben, ami az s hasznosságát (πi mellett) a következőképpen kapcsolja a szomszédai hasznosságához:
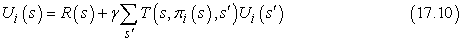
Például tegyük fel, hogy πi a 17.2. (a) ábrán látható eljárásmód. Ekkor azt kapjuk, hogy πi(1, 1) = Fel, πi(1, 2) = Fel és így tovább, illetve az egyszerűsített Bellman-egyenletek:
Ui(1, 1) = –0,04 + 0,8Ui(1, 2) + 0,1Ui(1, 1) + 0,1Ui(2, 1)
Ui(1, 2) = –0,04 + 0,8Ui(1, 3) + 0,2Ui(1, 2)
.
.
.
A lényeges az, hogy ezek az egyenletek lineárisak, mivel a „max” operátort eltávolítottuk. Ha az állapotok száma n, n lineáris egyenlet adódik n ismeretlennel, ami egzakt módon megoldható O(n3) időben standard lineáris algebrai módszerekkel.
Kis állapotterekre az eljárásmód-kiértékelés egzakt megoldómódszerekkel gyakran a leghatékonyabb megközelítés. Nagy állapotterekre az O(n3) idő megengedhetetlen lehet. Szerencsére nem szükséges egzakt eljárásmód-kiértékelést végezni. Ehelyett elvégezhetünk bizonyos számú egyszerűsített értékiterációs lépést (egyszerűsített, mivel az eljárásmód rögzített), hogy a hasznosságok elfogadhatóan jó becsléséhez jussunk. Az egyszerűsített Bellman-frissítés ehhez a folyamathoz a következő
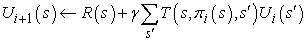
amit k-szor ismétlünk, hogy a következő hasznosságbecslés előálljon. Az adódó algoritmust módosított eljárásmód-iterációnak (modified policy iteration) nevezzük. Ez gyakran sokkal hatékonyabb, mint a szabványos eljárásmód-iteráció vagy értékiteráció.
Az eddig leírt algoritmusok megkövetelik a hasznosságok vagy eljárásmódok összes állapotbeli egyszerre történő frissítését. Megmutatható, hogy ez nem szigorúan szükséges. Valójában minden iterációnál kiválaszthatjuk az állapotok egy tetszőleges részhalmazát, és alkalmazhatjuk rá bármelyik fajta frissítést (eljárásmód-javítást vagy egyszerűsített értékiterációt). Ezt az általánosított algoritmust aszinkron eljárásmód-iterációnak (asynchronous policy iteration) nevezzük. A kezdeti eljárásmód és a hasznosságfüggvény adott feltételek melletti megválasztásánál az aszinkron eljárásmód-iteráció garantáltan konvergál az optimális eljárásmódhoz. A feldolgozandó állapotok megválasztásának szabadsága azt jelenti, hogy hatékonyabb heurisztikus algoritmusokat tervezhetünk – például olyan algoritmusokat, amelyek azon állapotok értékének frissítésére koncentrálnak, amelyeket egy jó eljárásmód valószínűleg elér. A valós életben ez nagyon hasznosnak tűnik: ha valakinek nincs szándékában a mélybe vetni magát egy szikláról, akkor nem kell aggódással töltenie az időt a bekövetkező állapotok pontos értékéről.


