17.1. Szekvenciális döntési problémák
Tételezzük fel, hogy egy ágens a 17.1. (a) ábrán látható 4 × 3-as környezetben helyezkedik el. A kezdő állapotból indulva minden időpontban választania kell egy cselekvést. A környezettel való interakció leáll, ha az ágens eléri a +1-gyel vagy a –1-gyel jelölt állapotot. Az egyes helyzetekben az elérhető cselekvések nevei: Fel, Le, Balra, Jobbra. Egyelőre feltételezzük, hogy a környezet teljesen megfigyelhető (fully observable), azaz az ágens mindig ismeri a helyzetét.
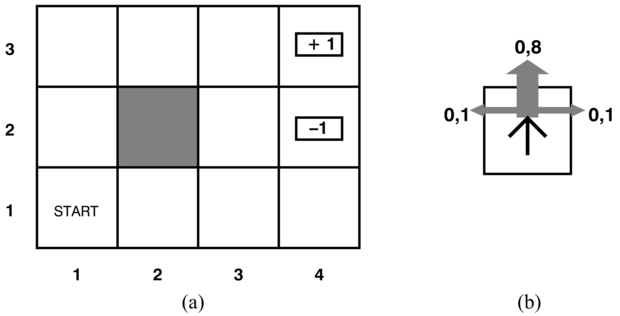
Ha a probléma determinisztikus volna, a megoldás könnyű lenne: [Fel, Fel, Jobbra, Jobbra, Jobbra]. Sajnos a környezet nem maradna mindig szinkronban ezzel a megoldással, mivel a cselekvések megbízhatatlanok. A véletlenszerű mozgás egy általunk elfogadott modelljét a 17.1. (b) ábra mutatja be. Minden cselekvés 0,8 valószínűséggel éri el a kívánt hatását, de a maradék esetben a cselekvések az ágenst a kívánt iránytól jobbra mozgatják. Továbbá, ha az ágens falba ütközik, akkor ugyanazon a mezőn marad. Például ha az (1, 1) kezdő négyzeten áll, a Fel cselekvés az ágenst az (1, 2)-re mozgatja 0,8 valószínűséggel, de 0,1 valószínűséggel a (2, 1)-re kerül, és 0,1 valószínűséggel balra megy, ahol is falnak ütközik és (1, 1)-en marad. Egy ilyen környezetben a [Fel, Fel, Jobbra, Jobbra, Jobbra] sorozat 0,85 = 0,32768 valószínűséggel kerüli meg az akadályokat, és éri el a (4, 3) célállapotot. Igen kis eséllyel az is megtörténhet, hogy a célt a másik úton keresztül éri el, 0,14 × 0,8, ami összességében 0,32776 valószínűséget jelent (lásd 17.1. feladat).
Az egyes állapotokban végrehajtott egyes akcióknak a kimeneti valószínűségeit állapotátmenet-modellnek (transition model) nevezzük, (vagy csak „modell”-nek, ha nem értelemzavaró). A T(s, a, s′) jelölést fogjuk használni annak a valószínűségnek a jelölésére, hogy az s állapotban az a cselekvés végrehajtása s′ állapotot eredményez. Feltesszük, hogy az átmenetek teljesítik a 15. fejezetben megfogalmazott Markov-tulajdonságot, azaz, hogy s′ elérése s-ből csak s-től függ, más korábbi állapotoktól már nem. Egyelőre a T(s, a, s′)-t tekinthetjük a valószínűségek egy nagy háromdimenziós táblázatának. Később, a 17.5. alfejezetben látni fogjuk, hogy az állapotátmenet-modell reprezentálható dinamikus Bayes-hálókkal (dynamic Bayesian network), csakúgy mint a 15. fejezetben.
Hogy teljessé tegyük a feladat környezetének a definiálását, meg kell adnunk az ágens hasznosságfüggvényét. Mivel a döntési probléma szekvenciális, a hasznosságfüggvény az állapotok sorozatától – a környezeti történettől (environment history) – fog függni, nem pedig egyetlen állapottól. A fejezetben később megvizsgáljuk az ilyen hasznosságfüggvények általános megadását; egyelőre egyszerűen kikötjük, hogy az ágens minden s állapotban egy R(s) jutalmat (reward) kap, ami lehet pozitív vagy negatív, de mindenképpen korlátos. A konkrét példánkban a jutalom minden állapotban –0,04, kivéve a végállapotokat (ahol +1 vagy –1). Egy környezeti történet hasznossága (egyelőre) egyszerűen a kapott jutalmak összege. Például ha az ágens a +1 állapotot 10 lépés után éri el, akkor az összhasznossága 0,6 lesz. A –0,04 negatív jutalom arra ösztönzi az ágenst, hogy minél gyorsabban érje el a (4, 3)-at, így ez a probléma a 3. fejezetbeli keresési problémák egy sztochasztikus általánosítása. Ez más megfogalmazásban úgy hangzik, hogy az ágens nem élvezi az életet ebben a környezetben, és olyan gyorsan ki akar kerülni, amilyen gyorsan csak lehet.
Egy teljesen megfigyelhető környezetben megadott szekvenciális döntési problémát Markov-állapotátmenet-modelljével és additív jutalmakkal Markov döntési folyamatnak neveznek (MDF) (Markov decision process). Egy MDF-et a következő három összetevő határoz meg:
Kezdőállapot: S0
Állapotátmenet-modell: T(s, a, s′)
Jutalomfüggvény:[171] R(s)
A következő kérdés az, hogyan néz ki egy megoldás a problémára? Azt már láttuk, hogy egy rögzített cselekvéssorozat nem oldja meg a problémát, mivel az ágens végül más állapotba jut a célállapot helyett. Ezért egy megoldásnak minden, az ágens által elérhető állapotra elő kell írnia, hogy az ágens mit tegyen. Egy ilyenfajta megoldás az eljárásmód (policy). Egy eljárásmódot általában π-vel jelölünk, és a π eljárásmód az s állapotban a π (s) cselekvést javasolja. Ha az ágens egy teljes eljárásmóddal rendelkezik, akkor függetlenül attól, hogy egy cselekvésnek mi is a kimenetele, az ágens mindig tudni fogja, mit tegyen a következő alkalommal.
Egy adott eljárásmód kezdőállapotból induló végrehajtása minden alkalommal egy különböző környezeti történetet eredményez a környezet sztochasztikus volta miatt. Egy eljárásmód minőségét ezért az adott eljárásmód generálta lehetséges környezeti történetek várható hasznosságával mérik. Az optimális eljárásmód (optimal policy) az az eljárásmód, ami a legnagyobb várható hasznosságot eredményezi. Az optimális eljárásmódot π *-gal jelöljük. A π * ismeretében az ágens úgy dönti el, hogy mit tegyen, hogy figyelembe veszi az aktuális érzékelését, ami az aktuális s állapotot közli vele, majd végrehajtja a π*(s) cselekvést. Az eljárásmód az ágens függvényét explicit módon reprezentálja, és ezért az voltaképpen egy egyszerű reflexágens leírása, amit egy hasznosságalapú ágens által használt információkból számítunk ki.
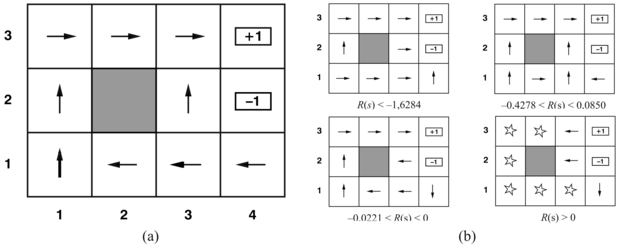
A 17.1. ábrán mutatott világ optimális eljárását a 17.2. (a) ábra mutatja. Látható, hogy mivel egy lépés költsége meglehetősen kicsi ahhoz a büntetéshez viszonyítva, hogy véletlenül a (4, 2) pozícióra kerülünk, az optimális eljárásmód a (3, 1) állapot esetén óvatos. Inkább egy hosszú kerülő út megtételét javasolja, mint a rövid átvágást a (4, 2) kockáztatásával.
A kockázat és a jutalom egyensúlyának megváltozása függ az R(s) értékétől a nem végső állapotoknál. A 17.2. (b) ábrán az R(s) értékének négy különböző intervallumához tartozó optimális eljárásmódot találhatunk. Ha R(s) ≤ –1,6284, akkor az élet anynyira elviselhetetlen, hogy az ágens egyenesen a legközelebbi kijárathoz tart, annak ellenére, hogy ez –1 értékű. Amikor –0,4278 ≤ R(s) ≤ –0,0850, az élet elég kellemetlen; az ágens a +1 állapothoz vezető utat választja, vállalva annak kockázatát, hogy esetleg a –1 állapotba kerül. Nevezetesen az ágens a (3, 1)-ben választja az átvágást. Amikor az élet csak kevéssé bánatos (–0,0221 < R(s) < 0), az optimális eljárásmód nem vállal semmilyen kockázatot. A (4, 1) és (3, 2) állapotokban az ágens teljesen elkerüli a –1 állapotot, így nem tud véletlenül beleesni, még ha ez azt is jelenti, hogy elég sokszor beveri a fejét a falba. Végül, ha R(s) > 0, akkor az élet kifejezetten élvezhető, és az ágens mindkét kijáratot elkerüli. Mindaddig, amíg a (4, 1), (3, 2) és (3, 3) állapotokban a cselekvések azok, amelyek az ábrán láthatók, minden eljárásmód optimális, és az ágens végtelen teljes jutalmat ér el, mivel soha nem lép be a végállapotba. Meglepő módon megmutatható, hogy hat más optimális eljárásmód is létezik az R(s) különböző intervallumaira. A 17.7. feladat kéri majd ezek megkeresését.
A kockázat és a jutalom óvatos egyensúlyozása az MDF-ek egy olyan meghatározó tulajdonsága, ami nem jelentkezik determinisztikus keresési problémáknál; másfelől ez meghatározó tulajdonsága számos valósvilág-beli döntési problémának. Emiatt az MDF-eket számos tudományterületen tanulmányozzák, ideértve az MI-t, az operációkutatást, a közgazdaságtant és a szabályozáselméletet. Algoritmusok tucatjait javasolták optimális eljárásmódok kiszámítására. A 17.2. és 17.3. alfejezetben leírunk a legfontosabb algoritmuscsaládok közül kettőt. Először azonban be kell fejeznünk a hasznosságok és eljárásmódok vizsgálatát a szekvenciális döntési problémák esetében.
A 17.1. ábrán látható MDF-példában az ágens teljesítményét a meglátogatott állapotokban kapott jutalmak összege mérte. Ez a teljesítménymérték nem önkényes, de nem is az egyetlen lehetőség. Ez az alfejezet a lehetséges alternatív teljesítménymértékeket vizsgálja – azaz alternatív hasznosságfüggvényeket a környezeti történéseken, amit úgy jelölünk, hogy Uh([s0, ..., sn]). Az alfejezet a 16. fejezetből származó ötleteken alapul, és a technikai részleteket is bemutatja; a főbb pontokat a végén összegezzük.
Fontos
Az első megválaszolandó kérdés az, hogy véges horizont (finite horizon) vagy végtelen horizont (infinite horizon) van a döntéshozatalnál. A véges horizont azt jelenti, hogy létezik egy rögzített N idő, ami után semmi nem érdekes – a játéknak vége, mondhatni. Így Uh([s0, ..., sN+k]) = Uh([s0, ..., sN]) minden k > 0 esetén. Például tegyük fel, hogy az ágens (3, 1)-ből indul a 17.1. ábra 4 × 3-as világában, és tegyük fel, hogy N = 3. Ekkor, hogy a +1 állapot elérésének legalább az esélye meglegyen, az ágensnek egyenesen felé kell tartani, és az optimális cselekvés a Fel. Ezzel szemben, ha N = 100, akkor bőségesen van idő a biztonságos utat követni Balra menve. Azaz, véges horizont esetében az optimális cselekvés egy adott állapotban idővel változhat. Azt mondjuk, hogy az optimális eljárásmód véges horizont esetében nem- stacionárius (nonstationary). Rögzített időkorlát hiányában ezzel szemben nincs ok különböző viselkedésre ugyanabban az állapotban más és más időpontokban. Így az optimális cselekvés csak az aktuális állapottól függ, és az optimális eljárásmód stacionárius (stationary). A végtelen horizontú esethez tartozó eljárásmódok ezért egyszerűbbek, mint a véges horizontú esethez tartozók, és ebben a fejezetben mi főként a végtelen horizontú esettel foglalkozunk.[172] Vegyük észre, hogy a „végtelen horizont” nem jelenti szükségszerűen azt, hogy az összes állapotsorozat végtelen; mindössze annyit jelent, hogy nincs egy rögzített határ. Nevezetesen, egy végtelen horizontú MDF-ben lehetnek végállapotot tartalmazó véges állapotsorozatok.
A következő eldöntendő kérdés az állapotsorozatok hasznosságának a kiszámítása. Tekinthetjük ezt a kérdést a többattribútumú hasznosságelmélet (multiattribute utility theory) egy kérdésének (lásd 16.4. alfejezet) azzal, hogy minden si állapotot az [s0, s1, s2, ...] állapotsorozat egy attribútumának veszünk. Egy egyszerű kifejezés eléréséhez, ami az attribútumokból épül fel, fel kell tételeznünk valamilyen preferenciafüggetlenséget. A legtermészetesebb feltevés az, hogy az ágens preferenciái az állapotsorozatok között stacionáriusok (stationary). A preferenciákra vonatkozó stacionaritás a következőket jelenti: ha két állapotsorozat, [s0, s1, s2,…] és 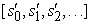 , ugyanazzal az állapottal kezdődik (például
, ugyanazzal az állapottal kezdődik (például 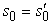 ), akkor a két sorozat a preferencia-sorrendjének ugyanannak kell lennie, mint az [s1, s2,…] és az
), akkor a két sorozat a preferencia-sorrendjének ugyanannak kell lennie, mint az [s1, s2,…] és az 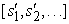 sorozatoknak. Ez tehát azt jelenti, hogy ha egy holnaptól kezdődő lehetséges jövőbeli eseménysort egy másik eseménysorral szemben preferálunk, akkor ez nem változhat, ha az eseménysor a mai naptól kezdődne. A stacionaritás egy meglehetősen ártalmatlannak tűnő feltevés, nagyon erős következményekkel: bizonyítható, hogy stacionaritás esetén a sorozatokhoz csak kétféle módon rendelhetők hasznosságok:
sorozatoknak. Ez tehát azt jelenti, hogy ha egy holnaptól kezdődő lehetséges jövőbeli eseménysort egy másik eseménysorral szemben preferálunk, akkor ez nem változhat, ha az eseménysor a mai naptól kezdődne. A stacionaritás egy meglehetősen ártalmatlannak tűnő feltevés, nagyon erős következményekkel: bizonyítható, hogy stacionaritás esetén a sorozatokhoz csak kétféle módon rendelhetők hasznosságok:
-
Additív jutalmak (additive rewards): egy állapotsorozat hasznossága ekkor
Uh([s0, s1, s2,...]) = R(s0) + R(s1) + R(s2) + …
A 17.1. ábra 4 × 3-as világa additív jutalmakat használ. Vegyük észre, hogy az additivitást hallgatólagosan kihasználtuk az utak költségfüggvényeinek felhasználásakor a heurisztikus keresési algoritmusokban (4. fejezet).
-
Leszámítolt jutalmak (discounted rewards): egy állapotsorozat hasznossága ekkor
Uh([s0, s1, s2,...]) = R(s0) + γR(s1) + γ2 R(s2) + …
ahol a γ leszámítolási tényező (discount factor) egy 0 és 1 közötti szám. A leszámítolási tényező fejezi ki egy ágens preferenciáját a jelenlegi és a jövőbeli jutalmak között. Amikor γ közel 0, akkor a távoli jövőbeli jutalmakat jelentéktelennek tekinti. Amikor γ értéke 1, akkor a leszámítolt jutalmak pontosan megegyeznek az additív jutalmakkal, így az additív jutalmak a leszámítolt jutalmak speciális esetei. A leszámítolás jó modellnek tűnik mind az állati, mind az emberi időbeli preferenciákra. Egy γ leszámítolási tényező ekvivalens egy (1/ γ) – 1 kamatlábbal.
A fejezet hátralevő részében leszámítolt jutalmakat fogunk feltételezni, aminek okai hamarosan világosak lesznek, bár néha megengedjük a γ = 1 értéket.
A végtelen horizont elfogadása mögött azonban rejlik egy probléma: ha a környezet nem tartalmaz egy végállapotot, vagy ha az ágens soha nem jut végállapotba, akkor az összes környezettörténet végtelen hosszú lesz, és a hasznosságok additív jutalmakkal általában végtelenek lesznek. Abban egyetérthetünk, hogy a +∞ jobb, mint a –∞, de két +∞ hasznosságú állapotsorozat összehasonlítása már bonyolultabb. Három megoldás kínálkozik, amelyek közül kettőt már láttunk:
-
Leszámítolt jutalmakkal egy végtelen sorozat hasznossága véges. Valójában, ha a jutalmakra létezik egy Rmax korlát és γ < 1, akkor azt kapjuk, hogy
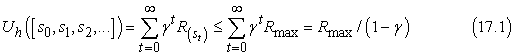
felhasználva a végtelen mértani sorozat összegképletét.
-
Ha a környezet tartalmaz végállapotokat, és ha garantált, hogy az ágens végül bekerül az egyikbe, akkor soha nem lesz szükségünk végtelen sorozatok összehasonlítására. Egy eljárásmódot, ami garantáltan végállapotba juttat, véges eljárásmódnak (proper policy) nevezünk. Véges eljárásmódoknál használhatjuk a γ = 1-t (azaz az additív jutalmakat). A 17.2. (b) ábrán látható első három eljárásmód véges, a negyedik azonban nem. Egy nem véges eljárásmód végtelen teljes jutalmat ér el a végállapotoktól való távolmaradással, amikor a nem végállapotok jutalma pozitív. A nem véges eljárásmódokra additív jutalmaknál nem mindig működnek az MDF-eket megoldó alapalgoritmusok, ami jó ok a leszámítolt jutalmak használatára.
-
Végtelen sorozatok összehasonlítására egy másik lehetőség az időegységenkénti átlagjutalom (average reward) felhasználása. Tegyük fel, hogy a 4 × 3-as világban az (1, 1) mező jutalma 0,1, míg más nem végállapotoké 0,01. Ekkor egy olyan eljárásmódnak, ami minden tőle telhetőt megtesz, hogy az (1, 1)-ben maradjon, nagyobb lesz az átlagos jutalma, mint annak, amelyik máshol marad. Az átlagos jutalom hasznos kritérium bizonyos problémákra, de az átlagjutalomra tervezett algoritmusok meghaladják e könyv kereteit.
Összegezve, a leszámítolt jutalmak használata jár a legkevesebb bonyodalommal az állapotsorozatok kiértékelésében. A végső lépés annak megmutatása, hogyan válaszszunk az eljárásmódok között, észben tartva azt, hogy egy adott π eljárásmód nem egyetlen állapotsorozatot generál, hanem a legkülönfélébb lehetséges állapotsorozatokat, mindegyiket egy adott valószínűséggel, amit a környezet állapotátmenet-modellje határoz meg. Így egy eljárásmód értéke a (sorozatonként) elért leszámítolt jutalmak várható értéke, ahol a várható érték képzése az összes állapotsorozat felett történik, ami az eljárás végrehajtása esetén előfordulhat. Egy π* optimális eljárásmód ekkor
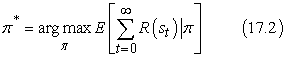
A következő két alfejezet algoritmusokat ír le az optimális eljárásmódok megtalálására.
[171] Az MDF egyes definíciói megengedik, hogy a jutalom függjön a cselekvéstől és a kimeneteltől is, így a jutalomfüggvény R(s, a, s′) alakú. Ez néhány környezet leírását egyszerűsíti, de a problémát alapvetően nem változtatja meg.
[172] Ez a teljesen megfigyelhető környezetekre igaz. Látni fogjuk, hogy a részlegesen megfigyelhető környezetekben a végtelen horizont esete nem annyira egyszerű.

