14.4. Egzakt következtetés Bayes-hálókban
Az alapvető feladat bármely valószínűségi következtető rendszer számára az, hogy kiszámítsa a célváltozók (query variables) egy halmazának a posteriori valószínűség-eloszlását egy adott megfigyelt esemény (event) esetén – azaz bizonyítékváltozók (evidence variables) egy halmazához történő érték-hozzárendelés esetén. A 13. fejezetben bevezetett jelölést fogjuk használni: X a célváltozót jelöli; E a bizonyítékváltozók E1, …, Em halmazát, e pedig a megfigyelt eseményt; Y fogja jelölni az (olykor rejtett változóknak (hidden variables) nevezett) nem-bizonyítékváltozók Y1, …, Yk halmazát. Így a változók teljes halmaza X = {X} ∪ E ∪ Y. Egy jellemző lekérdezés a P(X∣e) a posteriori eloszlásra irányul.[148]
A riasztós hálóban például megfigyelhetnénk azt az eseményt, ahol JánosTelefonál = igaz és MáriaTelefonál = igaz. Ekkor megkérdezhetnénk mondjuk a betörés megtörténtének a valószínűségét:
P(Betörés∣JánosTelefonál = igaz, MáriaTelefonál = igaz) = 〈0,284, 0,716〉
Ebben a fejezetben az a posteriori valószínűségek kiszámítására szolgáló egzakt algoritmusokat tárgyalunk, és átgondoljuk ennek a feladatnak a komplexitását. Kiderül, hogy általános esetben ez kivitelezhetetlen, ezért a 14.5. alfejezet közelítő következtetési módszereket ismertet.
A 13. fejezet elmagyarázta, hogy bármely feltételes valószínűség kiszámítható a teljes együttes eloszlás tagjainak összegzésével. Pontosabban, egy P(X∣e) lekérdezés megválaszolható a (13.6) egyenlet felhasználásával, amit a jobb követhetőség kedvéért itt megismétlünk:
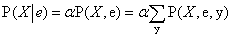
Fontos
Továbbá, mint ismeretes, a Bayes-háló a teljes együttes eloszlás egy teljes reprezentációját nyújtja. Még pontosabban, a (14.1) egyenlet azt mutatja, hogy az együttes eloszlás P(x, e, y) tagjai felírhatók a hálóból származó feltételes valószínűségek szorzataiként. Ezért egy lekérdezés megválaszolható a Bayes-háló felhasználásával, kiszámítva a hálóból származó feltételes valószínűségek szorzatainak az összegét.
A 13.4. ábrán a FELSOROL-EGYÜTTES-KÉRDEZÉS algoritmust adtuk meg a teljes együttes eloszlásból felsorolással történő következtetésre. Az algoritmus bemenetként fogadja a P teljes együttes eloszlást, és értékeket néz meg benne. Egyszerű módosítással elérhető, hogy az algoritmus egy bn Bayes-hálót fogad bemenetként, és az együttes bejegyzéseket a bn megfelelő FVT-bejegyzéseinek összeszorzásával „nézi meg”.
Vegyük a P(Betörés∣JánosTelefonál = igaz, MáriaTelefonál = igaz) lekérdezést. A rejtett változók ennél a kérdésnél a Földrengés és a Riasztás. A (13.6) egyenletből, a kifejezések rövidítése miatt a kezdőbetűket használva, azt kapjuk, hogy[149]
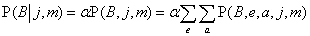
A Bayes-hálók szemantikája – (14.1) egyenlet – pedig az FVT-bejegyzések felhasználásával egy kifejezést ad. Az egyszerűség kedvéért ezt csak a Betörés = igaz esetére adjuk meg:
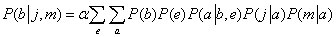
Ennek a kifejezésnek a kiszámításához négy tagot kell összeadnunk, amelyek mindegyikét öt szám összeszorzásával kapjuk. Legrosszabb esetben, amikor majdnem minden változó felett összegezni kell, az algoritmus komplexitása egy n bináris változós háló esetén O(n2n).
A következő egyszerű megfigyeléssel egy javításhoz juthatunk: a P(b) tag állandó, és ki lehet vinni az a és e feletti összegzések elé, a P(e) tag pedig kivihető az a feletti összegzés elé. Így azt kapjuk, hogy
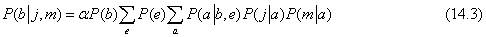
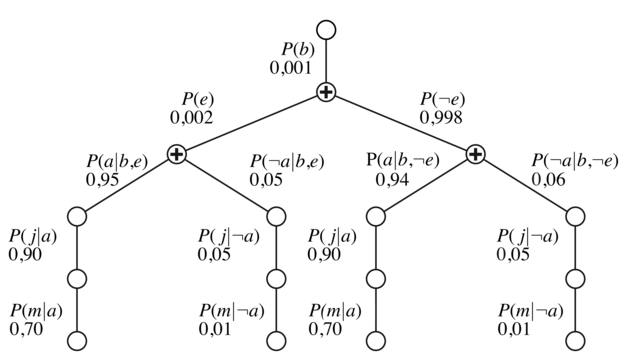
Ez a kifejezés egy ciklussal értékelhető ki, sorban végighaladva a változókon, miközben összeszorozzuk az FVT-bejegyzéseket. Minden összegzésnél, a változó lehetséges értékei szerint is iterálnunk kell. A számítás struktúráját a 14.8. ábra mutatja. Felhasználva a 14.2. ábra értékeit, azt kapjuk hogy P(b∣j,m) = α × 0,00059224. A ¬b-hez tartozó számítást átfutva az α × 0,0014919-et eredményez; így
P(B∣j,m) = α 〈0,00059224, 0,0014919〉 ≈ 〈0,284, 0,716〉
Azaz a betörés valószínűsége, ha mindkét szomszéd telefonál körülbelül 28%.
A 14.8. ábra a (14.3) egyenlet kiértékelési folyamatát mutatja, kifejezés fa alakban. A FELSOROL-KÉRDEZ algoritmus a 14.9. ábrán ilyen fákat mélységi rekurzióval értékel ki. Így a FELSOROL-KÉRDEZ tárkomplexitása csak lineáris a változók számában – az algoritmus így hatékonyan, anélkül összegez a teljes együttes eloszlás felett, hogy azt explicit módon megkonstruálná. Sajnos az algoritmus időkomplexitása egy n bináris változós hálónál minden esetben O(2n) – ami jobb, mint az egyszerű megközelítéshez tartozó O(n2n), de még mindig elég nyomasztó. Egy figyelemre méltó dolog a 14.8. ábra fájával kapcsolatban, hogy nyilvánvalóvá teszi a megismételt alkifejezéseket, amelyeket az algoritmus kiértékel. A P(j∣a) P(m∣a) és a P(j∣¬a) P(m∣¬a) szorzatok kétszer kerülnek kiszámításra, e minden értékénél. A következő fejezet egy általános módszert ír le, ami elkerüli az ilyen felesleges újraszámítások elvégzését.
A felsoroló algoritmus lényegesen javítható a 14.8. ábra által szemléltetett ismétlődő számítások kiküszöbölésével. Az ötlet egyszerű: egyszer végezzük el a számítást, és őrizzük meg az eredményeket későbbi használatra. Ez egyfajta dinamikus programozás. Ennek a megközelítésnek több változata is létezik; mi a legegyszerűbbet, a változó eliminációs (variable elimination) algoritmust mutatjuk be. A változó eliminálás a (14.3) egyenlet típusú kifejezéseket jobbról balra (azaz a 14.8. ábrán lentről felfelé) sorrendben értékeli ki. A köztes eredményeket eltároljuk, és bármely változó feletti összegzés a kifejezésnek csak azon része felett történik meg, amely függ ettől a változótól.
Szemléltessük ezt a folyamatot a betörés háló esetén. Értékeljük ki a következő kifejezést:
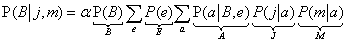
Vegyük észre, hogy a kifejezés minden részét megjelöltük a kapcsolódó változó nevével; ezeket tényezőknek (factors) nevezzük. A lépések a következők:
-
Az M tényező, P(m∣a) nem igényel M feletti összegzést (mivel M értéke már rögzített). Eltároljuk a valószínűséget a minden értékére egy kételemű vektorban,
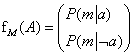
(Az fM azt jelöli, hogy f létrehozásában M-et felhasználtuk.)
-
Hasonlóan, tároljuk a J-hez tartozó tényezőt egy kételemű fJ(A) vektorban.
-
Az A-hoz tartozó tényező, P(a∣B, e), ami egy 2 × 2 × 2-es mátrix lesz, fA(A, B, E).
-
Most ki kell összegeznünk A-t ennek a három tényezőnek a szorzatából. Ez egy 2 × 2-es mátrixot eredményez, aminek indexei már csak B és E felett futnak. A mátrix nevében A-nál egy felülvonással jelezzük, hogy A már ki lett összegezve:
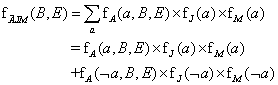
Az itt használt szorzást pontonkénti szorzásnak (pointwise product) nevezik, és hamarosan ismertetjük.
-
Hasonló módon dolgozzuk fel E-t: kiösszegezzük E-t fE(E) és
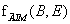 szorzatából:
szorzatából:
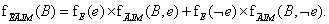
Most pedig kiszámíthatjuk az eredményt egyszerűen összeszorozva B tényezőjét (azaz fB(B) = P(B)-t) az 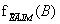 kiadódott mátrixszal:
kiadódott mátrixszal:
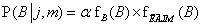
A 14.7. (a) feladatban azt kérjük, hogy ellenőrizze, helyes eredményt ad-e ez a folyamat.
A lépések sorozatát megvizsgálva láthatjuk, hogy két alapvető művelet szükséges: tényezőpárok pontonkénti összeszorzása és egy változó kiösszegzése tényezők szorzatából.
A pontonkénti szorzás nem mátrixszorzás és nem is egy elemenkénti szorzás. Két, f1 és f2 tényezőnek a pontonkénti szorzata egy új f tényezőt eredményez, amelynek változóit az f1 és f2 változóinak az uniója adja. Tételezzük fel, hogy a két tényezőben az Y1, ..., Yk változók közösek. Ekkor azt kapjuk, hogy
f(X1 … Xj, Y1 … Yk, Z1 … Zl) = f1(X1 … Xj, Y1 … Yk)f2(Y1 … Yk, Z1 … Zl)
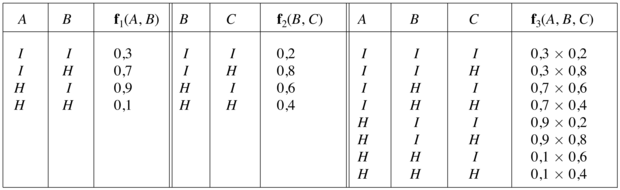
Ha minden változó bináris, akkor f1-nek és f2-nek 2j+k és 2k+l eleme van, pontonkénti szorzatuknak pedig 2j + k + l. Például az f1(A,B) és az f2(B,C) tényezők esetén a lentebb mutatott valószínűség-eloszlással, az f1 × f2 pontonkénti szorzata f3(A, B, C)-vel adott:
Egy változó kiösszegzése tényezők szorzataiból szintén egyértelmű számítás. Az egyetlen észreveendő trükk az, hogy bármely tényező, ami nem függ a kiösszegzendő változótól, az az összegzésen kívülre mozgatható. Például:
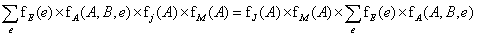
Most a pontonkénti szorzat kerül kiszámításra az összegzésen belül, a változót pedig kiösszegezzük a kiadódó mátrixból:
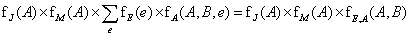
Vegyük észre, hogy mátrixokat nem szorzunk, ameddig nem kell kiösszegeznünk egy változót a kiadódó szorzatból. Annál a pontnál csak azokat a mátrixokat szorozzuk öszsze, amelyek magukban foglalják a kiösszegzendő változót. A pontonkénti szorzás és a kiösszegzés eljárások megléte esetén maga a változó eliminálás algoritmusa, amint azt a 14.10. ábra mutatja, igen egyszerűen felírható.
Nézzünk még egy lekérdezést: P(JánosTelefonál∣Betörés = igaz). Szokásos módon, az első lépés az egymásba ágyazott összegzések felírása:
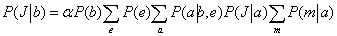
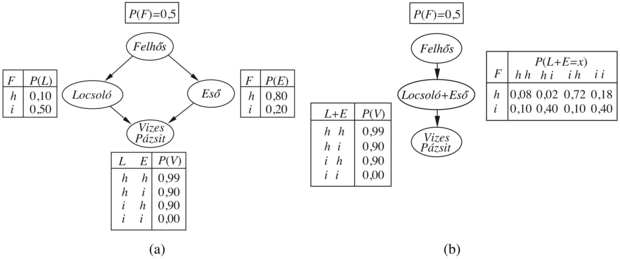
Ha ezt a kifejezést jobbról balra kiértékeljük, valami érdekeset veszünk észre: 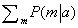 definíció szerint 1-gyel egyenlő. Így ezt eleve kihagyhattuk; a változó M a kérdésre irreleváns. Máshogy fogalmazva, a P(JánosTelefonál∣Betörés = igaz) lekérdezés eredményét nem változtatja meg a MáriaTelefonál eltávolítása a hálóból. Általában, bármely levélcsomópontot eltávolíthatunk, ami nem célváltozó vagy bizonyítékváltozó. Eltávolítás után lehetnek újabb levélcsomópontok, amelyek szintén irrelevánsak lehetnek.
definíció szerint 1-gyel egyenlő. Így ezt eleve kihagyhattuk; a változó M a kérdésre irreleváns. Máshogy fogalmazva, a P(JánosTelefonál∣Betörés = igaz) lekérdezés eredményét nem változtatja meg a MáriaTelefonál eltávolítása a hálóból. Általában, bármely levélcsomópontot eltávolíthatunk, ami nem célváltozó vagy bizonyítékváltozó. Eltávolítás után lehetnek újabb levélcsomópontok, amelyek szintén irrelevánsak lehetnek.
Fontos
Ezt az eljárást folytatva végül szükségszerűen arra jutunk, hogy minden változó, ami nem őse a célváltozónak vagy egy bizonyítékváltozónak, irreleváns a lekérdezésre. A változó elimináló algoritmus ezért az összes ilyen változót eltávolíthatja a lekérdezés kiértékelése előtt.
Megmutattuk, hogy a változóeltávolítás hatékonyabb, mint a felsorolás, mivel elkerüli a számítások megismétlését (ahogyan az irreleváns változókat is kiejti). A változó eliminálás idő- és tárigényét az algoritmus működése alatt létrejövő legnagyobb tényező mérete befolyásolja a legerőteljesebben. Ezt viszont a változók eliminálásának sorrendje és a háló struktúrája határozza meg.
Fontos
A 14.2. ábra betörős hálója a hálóknak azon családjához tartozik, ahol a háló bármely két csomópontja között legfeljebb egyetlen irányítatlan út létezik. Ezeket egyszeresen összekötött (singly connected) hálóknak vagy polifáknak (polytree) nevezzük, amelyeknek van egy különösen kellemes tulajdonságuk: az egzakt következtetés idő- és tárkomplexitása a polifákban a háló méretében lineáris. Itt a méret az FVT-bejegyzések számával van definiálva; ha minden egyes csomópont szüleinek a száma egy konstanssal korlátozott, akkor a komplexitás a csomópontok számában is lineáris. Ezek az eredmények bármely – a háló topológiai sorrendjével konzisztens – sorrendezés esetén fennállnak (lásd 14.7. feladat).
Fontos
A többszörösen összekötött (multiply connected) hálóban (lásd például 14.11. (a) ábra) a változó eliminálás legrosszabb esetben exponenciális idő- és tárkomplexitású lehet, még akkor is, ha a csomópontonkénti szülők száma korlátos. Ez nem meglepő, figyelembe véve, hogy a Bayes-hálókban való következtetés NP-nehéz, mivel ez speciális alesetként tartalmazza az ítéletlogikai következtetést is. Valójában megmutatható (lásd 14.8. feladat), hogy a probléma ugyanannyira nehéz, mint kiszámítani egy ítéletlogikai formula esetén a formulát kielégítő értékadások számát. Ez azt jelenti, hogy ez #P-nehéz („számosság-P-nehéz”), azaz szigorúan nehezebb, mint az NP-teljes problémák.
Szoros kapcsolat áll fenn a Bayes-hálókban történő következtetés komplexitása és a kényszerkielégítési problémák (CSP) komplexitása között. Amint az 5. fejezetben tárgyaltuk, egy diszkrét CSP megoldásának nehézsége ahhoz kapcsolódik, hogy a kényszergráf mennyire „faszerű”. Olyan mértékek, mint a hiperfaszélesség (hypertree width), amelyek a CSP megoldási komplexitását határolják, közvetlenül alkalmazhatók Bayes-hálóknál is. Ezenfelül a változó eliminálás algoritmusa általánosítható úgy, hogy kényszerkielégítési problémákat is és Bayes-hálókat is megoldjon.
A változó eliminálás algoritmusa egyszerű és hatékony egyedi lekérdezések megválaszolására. Azonban ha a háló összes változójának az a posteriori eloszlását szeretnénk kiszámítani, akkor kevésbé hatékony is lehet. Például egy polifa hálóban O(n) egyenként O(n) költségű lekérdezést kell kiadni, összességében O(n2) időköltséggel. Csoportosító (clustering) eljárásokkal (amit egyesítési fa – join tree – algoritmusnak is neveznek) ez az idő O(n)-re csökkenthető. Emiatt ezeket az algoritmusokat gyakran használják kereskedelmi Bayes-hálós eszközökben.
A csoportosítás alapötlete, hogy a háló önálló csomópontjait egyesítjük, klasztercsomópontokat formálva úgy, hogy a kiadódó háló polifa legyen. Például a 14.11. (a) ábrán mutatott, többszörösen összekötött háló egy polifává konvertálható a Locsoló és az Eső csomópontok egy Locsoló+Eső-nek nevezett klasztercsomópontba (cluster node) való összevonásával, ahogy azt a 14.11. (b) ábra mutatja. A két bináris csomópontot egyetlen megacsomópont váltotta fel, ami négy lehetséges értéket vesz fel: hh, hi, ih, ii. A megacsomópontnak csak egy szülője van, a bináris Felhős változó, így két feltételes eset létezik.
A háló polifává konvertálása után, egy speciális célú következtetési algoritmust alkalmazunk. Alapvetően az algoritmus egyfajta kényszerterjesztés (lásd 5. fejezet), ahol a kényszerek biztosítják, hogy a szomszédos csoportokban megegyeznek a közös változók a posteriori eloszlásai. Gondos nyilvántartással ez az algoritmus képes O(n) időben – ahol n most a módosított háló mérete – kiszámolni a háló összes nem bizonyíték csomópontjának a posteriori eloszlását. Azonban a probléma NP-nehéz volta nem tűnt el: ha a háló exponenciális idő- és tárigényű a változó eliminálás esetén, akkor a csoportosított hálóhoz tartozó FVT-k megkonstruálása exponenciális idő- és tárigényű lesz.
[148] Feltesszük, hogy a célváltozó nincs a bizonyítékváltozók között; amúgy X a posteriori eloszlása a megfigyelt értékre 1 valószínűséget ad. Az egyszerűség kedvéért azt is feltettük, hogy a kérdés egyetlen változóra irányul. Az algoritmusaink könnyen kiterjeszthetők több változó együttesének lekérdezésére.
[149] Egy olyan kifejezés mint a 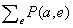 a P(A = a, E = e) -nek az összegzését jelenti minden lehetséges e értékre. Ez többértelműséget rejt magában, mivel a P(e) jelölést használják mind a P(E = igaz), mind a P(E = e) jelentés kifejezésére, azonban a szándékolt jelentésnek a szövegkörnyezetből ki kell derülnie; egy összegzés esetében az utóbbiról van szó.
a P(A = a, E = e) -nek az összegzését jelenti minden lehetséges e értékre. Ez többértelműséget rejt magában, mivel a P(e) jelölést használják mind a P(E = igaz), mind a P(E = e) jelentés kifejezésére, azonban a szándékolt jelentésnek a szövegkörnyezetből ki kell derülnie; egy összegzés esetében az utóbbiról van szó.



