Ebben az alfejezetben a valószínűségi következtetés (probabilistic inference) egy egyszerű módszerét fogjuk leírni – hogy hogyan határozhatók meg az állítások a posteriori valószínűségekre vonatkozó megfigyelt bizonyítékok alapján. „Tudásbázisként”, a teljes együttes valószínűség-eloszlást fogjuk használni, amelyből az összes kérdésre adandó válasz levezethető. Menet közben számos hasznos, a valószínűségeket tartalmazó egyenletek kezelésére alkalmas módszert is bevezetünk.

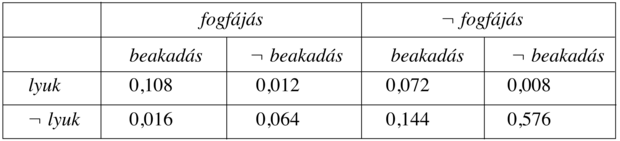
Kezdjük egy egészen egyszerű példával, egy olyan tartománnyal, amely mindössze három logikai változóból áll. Ezek: Fogfájás, Lyuk, Beakadás (a fogorvos kellemetlen acélszondája beleakad a fogamba). A teljes együttes eloszlás a 13.3. ábra szerinti 2 × 2 × 2-es táblázatból fog állni.

Vegyük észre, hogy az együttes valószínűség-eloszlásban – a valószínűségi axiómáknak megfelelően – a valószínűségek összege 1. Hasonlóképpen, a (13.2) egyenlet közvetlen módot nyújt bármely, egyszerű vagy összetett állítás valószínűségének a meghatározására: egyszerűen azokat az elemi eseményeket kell meghatároznunk, amelyekben az állítás igaz, majd összegeznünk kell a hozzájuk rendelt valószínűségeket. Például, hat olyan elemi esemény van, amelyben a lyuk ∨ fogfájás igaz:

P(lyuk ∨ fogfájás) = 0,108 + 0,012 + 0,072 + 0,008 + 0,016 + 0,064 = 0,28

Az egyik általános feladat a változók egy részhalmaza vagy egyetlen változó fölötti valószínűségi eloszlás kifejezése. Például az első sor bejegyzéseinek összege a lyuk feltétel nélküli vagy peremeloszlását^[140] (marginal probability) adja:

P(lyuk) = 0,108 + 0,012 + 0,072 + 0,008 = 0,2

Ezt a folyamatot marginalizálásnak (marginalization) vagy kiátlagolásnak (summing out) hívjuk, mivel a Lyuk-on kívüli változókat „kiátlagoljuk”. A következő általános behatárolási szabályt fogalmazhatjuk meg a változók tetszőleges Y és Z halmaza esetén:

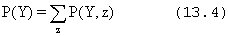
Azaz, egy Y feletti eloszlás megkapható, ha az összes többi változót kiátlagoljuk az Y-t tartalmazó együttes eloszlásokból a szorzat szabályban

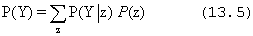
Ezt a szabályt feltételfeloldásnak (conditioning) hívjuk. A marginalizálás és a feltételfeloldás szabályai előnyöseknek fognak bizonyulni mindenfajta valószínűségi kifejezéseket tartalmazó következtetésben.

A legtöbb esetben valamely változó, bizonyos másokra vonatkozó tények esetén fennálló, feltételes valószínűségének kiszámítása fog bennünket érdekelni. A feltételes valószínűségek meghatározásához, először is alkalmazzuk a (13.1) egyenletet, hogy egy feltétel nélküli valószínűségen alapuló kifejezésre jussunk, majd ezen kifejezés értékét meghatározzuk a teljes együttes eloszlásból. Például a lyuk valószínűségét a fogfájás tény fennállása esetére az alábbiak szerint határozhatjuk meg:

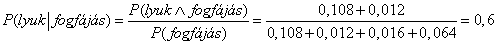
Ellenőrzésképpen kiszámíthatjuk annak valószínűségét, hogy nincs lyuk, de tudjuk, hogy fogfájás igen:

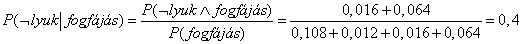
Vegyük észre, hogy a fenti két számításban az 1/P(fogfájás) konstans értékű marad függetlenül attól, hogy a Lyuk mely értékét számítjuk. Valójában ez egy, a P(Lyuk∣fogfájás)-t normalizálás (normalization) konstansnak tekinthető, amely biztosítja, hogy a feltételes valószínűségek összege 1 lesz. A valószínűségekkel foglalkozó fejezetekben az ilyen konstansokat a-val fogjuk jelölni. E jelölés segítségével a két előző kifejezés egybefoglalható:

P (Lyuk∣fogfájás) = αP (Lyuk, fogfájás)

= α[P(Lyuk, fogfájás, beakadás) + P(Lyuk, fogfájás, ¬beakadás)]

= α[〈0,108, 0,016〉 + 〈0,012, 0,064〉 = α〈0,12, 0,08〉 = 〈0,6, 0,4〉

A normalizálás sok valószínűségi számításnál hasznos rövidítésnek bizonyul.

A példából levezethető egy általános következtetési eljárás. Ragaszkodjunk ahhoz az esethez, ahol a keresés egy változót érint. A következő jelölésekre lesz még szükségünk: jelölje X a keresés változóját (a példában ez a Lyuk), E jelentse a tény változók halmazát (a példában a Fogfájás az egyetlen ilyen), e ezek megfigyelt értékét mutatja és a többi, meg nem figyelt változót Y foglalja magában (a példa esetében csak a Beakadás tartozik ide). P(X∣e)-t keressük, és a következőképpen számíthatjuk ki:

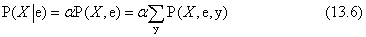
ahol az összegzést az összes lehetséges y fölött végezzük (azaz az Y meg nem figyelt változók értékeinek összes lehetséges kombinációja esetén). Vegyük észre, hogy az X, E és Y változó együttesen a változók teljes halmazát alkotja az adott tárgytartományban, így P(X, e, y) egyszerűen a teljes valószínűségi eloszlás egy valószínűségi részhalmaza. Az algoritmust a 13.4. ábra mutatja.

Az eljárás ciklusa mind X, mind Y összes értéke fölött fut, számba véve minden olyan elemi eseményt, amely e rögzített értéke mellett lehetséges, az együttes valószínűségi tábla alapján összegzi ezek valószínűségeit, és normalizálja az eredményeket.

Ha adott a teljes együttes valószínűségi eloszlás, akkor a FELSOROL-EGYÜTTES-KÉRDEZÉS egy teljes algoritmus, amely alkalmas minden diszkrét változóra vonatkozó valószínűségi lekérdezés megválaszolására. Azonban nem minősíthető jónak: egy n db Boole-típusú logikai változó által leírt tartományban O(2ⁿ) méretű bemeneti táblára van szüksége, és a tábla feldolgozása is O(2ⁿ) időt igényel. Valós problémák esetén nem csupán három, hanem több száz vagy több ezer véletlen változó figyelembevételére van szükség. Nagyon hamar teljesen kivitelezhetetlenné válik a szükséges hatalmas számú valószínűség definiálása – nem létezik ugyanis olyan tapasztalat, amellyel a táblázat egyes bejegyzései külön-külön becsülhetők lennének.

Ezért a táblázatos formában megadott teljes együttes valószínűségi eloszlás a gyakorlatban nem használható eszköz következtető rendszerek felépítésére (mindemellett a fejezet végén található történeti megjegyzésekben találkozhatunk egy ilyen módszeren alapuló valós alkalmazással). E technikát úgy kell tekintenünk, mint egy elméleti alapot, amelyre a hatékonyabb módszerek épülhetnek. A fejezet további részeiben bemutatjuk azokat az alapötleteket, amelyekre szükségünk lesz a 14. fejezet valós rendszereinek kifejlesztéséhez.