11.4. Tervkészítési gráfok

Az összes javasolt heurisztika a teljesen rendezett és a részben rendezett tervkészítésre pontatlanságokkal terhelt. Ez a fejezet bemutatja, hogy egy speciális adatszerkezet a tervkészítési gráf (planning graph) felhasználható, hogy jobb heurisztikus becsléseket nyerjünk. Ezek a heurisztikák bármely eddig tárgyalt keresési technikával használhatók. Egy másik lehetőség, hogy a megoldást közvetlenül a tervkészítési gráfból nyerjük ki egy erre kiélezett algoritmussal, mint amilyen például a GRAPHPLAN.

A tervkészítési gráf a terv időrendi lépéseinek megfelelő szintekből áll, ahol a 0-dik szint a kiinduló állapot. Minden szin egy literálhalmazt és egy cselekvéshalmazt tartalmaz. A literálok durván azok, melyek igazak lehetnek az adott lépésnél, az addig végrehajtott cselekvések függvényében. Ismét durván fogalmazva, a cselekvések azok, melyeknek az előfeltételei teljesülhetnek az adott időlépésben attól függően, hogy aktuálisan mely literálok teljesülnek. Azért mondjuk, hogy „durván”, mert a tervkészítési gráf csak a cselekvések közötti lehetséges negatív kölcsönhatások egy korlátozott részhalmazát tartalmazza, ezért a tervkészítési gráf optimista lehet a literál teljesítéséhez szükséges minimális lépések számával kapcsolatban. Mindazonáltal a tervkészítési gráfban ez a lépésszám egy jó becslés arra, hogy milyen nehéz egy literált teljesíteni a kiindulási állapotból. Még fontosabb, hogy a tervkészítési gráfot úgy definiáltuk, hogy könnyen elkészíthető legyen.

A tervkészítési gráf csak ítéletlogikai tervkészítési problémákra alkalmazható – olyanokra, melyek nem tartalmaznak változókat. Ahogy a 11.1. alfejezetben említettük, mind a STRIPS, mind az ADL reprezentáció ítéletlogikára alakítható. A nagyszámú entitást tartalmazó problémákat ez jelentősen felduzzaszthatja a cselekvéssémák számában. Ennek ellenére a tervkészítési gráfok hatékony eszköznek bizonyultak a nehéz tervkészítési problémák megoldásában.

A tervkészítési gráfokat egy egyszerű példán mutatjuk be. (Az összetettebb feladatok olyan gráfhoz vezetnek, amelyek nem férnének ki egy oldalra.) A 11.11. ábra a feladatot, míg a 11.12. ábra az ehhez tartozó gráfot mutatja. Az S0 állapotszintről indulunk, ami a probléma kiinduló állapotának felel meg. Ezt az A0 cselekvésszinttel folytatjuk, amibe azokat a cselekvéseket helyezzük, melyek előfeltételei az előző szinten teljesülnek. Minden cselekvés össze van kötve az S0-ban található előfeltételeivel, illetve az S1-ben található következményeivel, ami ebben az esetben az S0-ban nem szereplő literálok bevezetését jelenti S1-ben.

11.11. ábra - A „legyen süti és együnk is” probléma
A „legyen süti és együnk is” probléma

A tervkészítési gráfnak a nem cselekvést ugyanúgy kell reprezentálni, mint a cselekvéseket. Ez annyit tesz, hogy a szituációkalkulus keretaxiómáinak megfelelő működésre van szükség, ami alapján egy literál két állapon keresztül igaz maradhat, ha nincs ezt módosító cselekvés. Egy tervkészítési gráfban ezt megőrző cselekvésekkel (persistence actions) oldjuk meg. Minden pozitív és negatív C literálhoz egy megőrző cselekvést szúrunk be C előfeltétellel és C következménnyel. A 11.12. ábra az A0 szinten egyetlen „valós” cselekvést az Eszik(Süti)-t tartalmazza, két megőrző cselekvéssel, amit kicsi négyzetek jelölnek.

Az A0 tartalmazza az összes cselekvést, ami az S0 állapotban előfordulhat, de ugyanilyen fontos, hogy rögzíti a cselekvések közötti ütközéseket is, amelyek megakadályozzák, hogy egyszerre történjenek. A 11.12. ábra szürke vonalai ezeket a kölcsönös kizárási (mutual exclusions vagy mutex) kapcsolatokat jelölik. Például az Enni(Süti) kölcsönös kizárásban van a Van(Süti) vagy a ¬Megevett(Süti) megőrzésével. Hamarosan látjuk, hogy a mutex kapcsolatokat hogyan számíthatjuk.

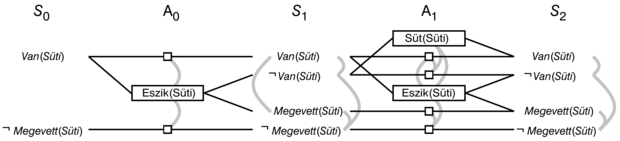
11.12. ábra - A „legyen süti és együnk is” probléma tervkészítési gráfja az S2 szintig. A téglalapok az akciókat jelentik (a kicsi négyzetek a megőrző cselekvések), az egyenesek az előfeltételeket és a következményeket jelölik. A kölcsönös kizárásokat ívelt szürke vonalak jelölik.
A „legyen süti és együnk is” probléma tervkészítési gráfja az S2 szintig. A téglalapok az akciókat jelentik (a kicsi négyzetek a megőrző cselekvések), az egyenesek az előfeltételeket és a következményeket jelölik. A kölcsönös kizárásokat ívelt szürke vonalak jelölik.

Az S1 az összes olyan literált tartalmazza, ami az A0 szint akcióinak bármely részhalmazát választva elérhető. Szintén tartalmaz mutex kapcsolatokat (szürke vonalakat) jelölve az olyan literálokat, melyek nem teljesülhetnek egyszerre, a választott cselekvésektől függetlenül. Például a Van(Süti) és a Megevett(Süti) kölcsönösen kizárják egymást. Az A0 kiválasztott cselekvéseitől függően az eredmény vagy az egyik vagy a másik lehet, de a kettő egyszerre nem. Más szavakkal az S1, csakúgy, mint a regressziós állapottér-keresés, több állapotot reprezentál, a kizárási kapcsolatok pedig kényszerek, melyek a lehetséges állapotok halmazát definiálják.

És ez így megy tovább. Az Si állapot- és az Ai cselekvésszintek között mozgunk, egészen addig, míg elérünk egy szintet, ahol két egymást követő szint azonos. Ekkor azt mondjuk, hogy a gráf kiegyenlítődött (leveled off). Minden egymást követő szint azonos, így további kiterjesztésre nincsen szükség.

Egy olyan struktúrát kaptunk, ahol az Ai szint tartalmaz minden Si-ben alkalmazható cselekvést, a kényszerekkel együtt, melyek megmondják, hogy melyik cselekvéspár nem hajtható végre egyidejűleg. Minden Si szint tartalmazza az összes literált, ami az Ai–1 összes lehetséges cselekvéshalmazának hatására teljesül, a kényszerekkel együtt, amelyek a nem lehetséges literálpárokat jelölik ki. Fontos megjegyezni, hogy a tervkészítési gráf elkészítési folyamatához nem kell választanunk a cselekvések között, ami kombinatorikus keresést eredményezne. Ezzel szemben, a tervkészítési gráf konstrukciója csak a lehetetlen választásokat rögzíti, mutex kapcsolatok felhasználásával. Egy ilyen tervkészítési gráf elkészítésének bonyolultsága egy alacsonyrendű polinomiális komplexitás a cselekvések számát tekintve, ahol az állapottér exponenciális a literálok számában.

Most mutex kapcsolatokat definiálunk, mind a cselekvések, mind a literálok számára. Egy adott szinten, a mutex kapcsolat akkor érvényes két cselekvés között, ha a következő három feltétel valamelyike fennáll:

  • Inkonzisztens hatások: egy cselekvés negálja egy másik következményét. Például az Eszik(Süti) és a Van(Süti) megőrzése inkonzisztens hatású, mert a Van(Süti) következmény tekintetében ellentétesek.

  • Interferencia: egy cselekvés egyik következménye a negálása egy másik cselekvés előfeltételének. Például az Eszik(Süti) interferál a Van(Süti) megőrzésével, mert negálja az előfeltételét.

  • Versenyhelyzet: egy cselekvés előfeltétele kölcsönösen kizáró egy másik előfeltételével. Például a Süt(Süti) és az Eszik(Süti) mutexek, mert versenyeznek a Van(Süti) előfeltétel tekintetében.

Két azonos szineten lévő literál között mutex kapcsolat áll fenn, ha az egyik a másik negáltja, vagy bármely lehetséges cselekvéspár, amely a két literált elérheti, egymást kölcsönösen kizáró. Ezt az állapotot inkonzisztens háttérnek nevezzük. Például a Van(Süti) és a Megevett(Süti) kizárják egymást S1-ben, mert az egyetlen mód a Van(Süti) teljesítésére egy megőrző cselekvés, ami mutex a Megevett(Süti) egyetlen elérési lehetőségével, nevezetesen az Eszik(Süti) cselekvéssel. Az S2 szinten a két literál már nem mutex, mert új elérési lehetőségek vannak hozzájuk, mint a Süt(Süti) és a Megevett(Süti) megőrző cselekvése, melyek nem zárják ki egymást.

11.4.1. Tervkészítési gráfok heurisztikus becslésekre

Fontos

A tervkészítési gráf, ha egyszer már létrehoztuk, nagyon gazdag információforrás a problémáról. Például egy literál, ami nem található meg az utolsó szinten, egyetlen tervvel sem érhető el. Ez a megfigyelés a visszafelé keresésben használható a következőképp: bármely elérhetetlen literált tartalmazó állapot költsége h(n) = ∞. Hasonlóan a részben rendezett tervkészítésnél bármely tervnek a költsége egy elérhetetlen nyitott előfeltétellel, h(n) = ∞.

Ez az ötlet tovább általánosítható. Minden cél literál elérési költségét becsülhetjük azzal a szinttel, ahol először megjelenik a tervkészítési gráfban. Ezt a cél szint költségének (level cost) nevezzük. A 11.12. ábrán a Van(Süti) szint költsége 0, a Megevett(Süti) szint költsége 1. Könnyű megmutatni (lásd 11.9. feladat), hogy ezek a közelítések elfogadhatók az egyedülálló célokra. A becslés azonban lehet, hogy nem túl jó, mert a tervkészítési gráfok több cselekvést megengednek szintenként, míg a heurisztika csak a szintek számát tartalmazza, és nem a cselekvések számát. Ebből kifolyólag a heurisztikák számításában, gyakori a soros tervkészítési gráf (serial planning graph) használata. A soros gráf szerint egy adott időpillanatban csak egyetlen cselekvés hajtható végre, ami mutexekkel érhető el úgy, hogy a megőrző cselekvések kivételével, minden cselekvés közé mutex kapcsolatot teszünk. A soros tervkészítő gráfból kinyert szintköltségek gyakran egész elfogadható közelítését adják a valós költségeknek.

Három egyszerű megközelítés létezik, hogy célliterálok konjunkcióihoz költséget becsüljünk. A maximális szint (max-level) heurisztika egyszerűen a célok közüli maximális szintköltségét veszi, ami elfogadható, de nem feltétlen nagyon pontos. A szintösszeg (level sum) heurisztika a részcél függetlenségi feltételezésből a célok szintköltségeinek összegét adja. Ez nem elfogadható, de nagyon jól működik olyan gyakorlati problémákra, amelyek nagymértékben részekre bonthatók. Ez sokkal pontosabb, mint a 11.2. alfejezetben bemutatott nem-kielégített-célok-heurisztika. A mi feladatunkban a Van(Süti) ∧ Megevett(Süti) konjunktív célhoz rendelhető heurisztikus becslés 0 + 1 = 1, míg a helyes válasz 2. Mindezeken túl, ha eltávolítjuk a Süt(Süti) cselekvést, a becslés még mindig 1, de a konjunktív cél ekkor már elérhetetlen. Végezetül, a halmazszint (set-level) heurisztika azt a szintet keresi meg, ahol a konjunktív cél összes literálja megjelenik a tervkészítési gráfban, és nincsenek közöttük kölcsönösen kizáró párok. A heurisztika a korrekt 2 értéket adja az eredeti feladatra és végtelent a Süt(Süti) nélküli feladatra. Ez előnyben van a maximális szint heurisztikával szemben, és kimagaslóan jól működik azon feladatokban, ahol sok kölcsönhatás van a résztervek között.

Lévén egy pontos heurisztika készítésére szolgáló eszköz, a tervkészítési gráf tekinthető úgy, mint egy relaxált probléma, ami hatékonyan megoldható. Hogy a relaxált probléma természetét megértsük, pontosan meg kell értenünk, hogy mit jelent, ha egy g literál megjelenik a tervkészítési gráf Si szintjén. Ideális esetben garanciát szeretnénk arra, hogy létezik egy terv i cselekvés szinttel, ami eléri g-t, illetve ha g nem jelenik meg, akkor nincs is ilyen terv. Sajnos ezt garantálni majdnem ugyanolyan nehéz, mint megoldani az eredeti tervkészítési problémát. A tervkészítési gráf a garancia második részéről gondoskodik (ha g nem jelenik meg, akkor nincs terv), de ha g megjelenik, akkor a tervkészítési gráf csak annyit ígér, hogy van egy terv, ami várhatóan eléri g-t, nincsenek „nyilvánvaló” hibák. Egy nyilvánvaló hiba definíció szerint egy olyan hiba, ami úgy detektálható, hogy két cselekvést vagy két literált tekintünk egyszerre, vagy más szavakkal a mutex relációkat vizsgáljuk. Lehetnek összetettebb hibák, melyek három, négy vagy több cselekvést tartalmaznak, de a tapasztalatok azt mutatják, hogy nem éri meg ezekkel foglalkozni. Ez hasonló a kényszerkielégítési problémáknál tanultakkal, hogy a megoldás megkeresése előtt gyakran megéri a 2-konzisztencia számítás, de a 3- vagy a magasabb konzisztencia kiszámítása ritkábban kifizetődő (lásd 5.2. alfejezet).

11.4.2. A Graphplan algoritmus

Ez a fejezet bemutatja, hogy hogyan nyerhető ki közvetlenül a terv a tervkészítési gráfból, ahelyett hogy azt csak a heurisztikákhoz használjuk. A GRAPHPLAN algoritmusnak (11.13. ábra) két fő lépése van, melyek ciklikusan váltakoznak. Először ellenőrzi, hogy minden célliterál jelen van-e az adott szinten anélkül, hogy mutex kapcsolatok lennének közöttük. Ebben az esetben, az aktuális gráfban létezhet megoldás, így az algoritmus megpróbálja azt kinyerni. Ellenkező esetben bővíti a gráfot úgy, hogy az aktuális szinthez a cselekvéseket, a következőhöz az állapotliterálokat adja: ez a folyamat folytatódik addig, amíg megtaláljuk a megoldást, vagy bebizonyosodik, hogy nem létezik megoldás.

11.13. ábra - A GRAPHPLAN algoritmus. A GRAPHPLAN algoritmus egy megoldás kinyerő és egy gráf-bővítő lépés között alternál. A MEGOLDÁS-KINYERÉS a befejezéstől visszafelé keresve ellenőrzi, hogy található-e megoldás. A GRÁF-BŐVÍTÉS adja a cselekvéseket az adott szinthez és az állapotliterálokat a következőhöz.
A GRAPHPLAN algoritmus. A GRAPHPLAN algoritmus egy megoldás kinyerő és egy gráf-bővítő lépés között alternál. A MEGOLDÁS-KINYERÉS a befejezéstől visszafelé keresve ellenőrzi, hogy található-e megoldás. A GRÁF-BŐVÍTÉS adja a cselekvéseket az adott szinthez és az állapotliterálokat a következőhöz.

Kövessük végig a GRAPHPLAN működését a 11.1. alfejezet kerékcsere problémáján! A teljes gráf a 11.14. ábrán látható. A GRAPHPLAN első lépésben inicializálja a tervkészítési gráfot egy egyszintű (S0 szint) gráfra, ami a kiindulási állapot öt literálját tartalmazza. Az Ott(Pótkerék, Tengely) célliterál nincs jelen az S0-ban, ezért nem kell meghívnunk a MEGOLDÁS-KINYERÉST, hiszen biztosak vagyunk benne, hogy még nincs megoldás. Ehelyett a GRÁF-BŐVÍTÉS hozzáad három cselekvést, melyeknek az előfeltétele már teljesül az S0 szinten (például az összes cselekvés, kivéve a Felszerel(Pótkerék, Tengely) – cselekvést). Hozzáadja továbbá a megőrző-cselekvéseket S0 összes literáljához. A cselekvések következményeit az S1 szinthez adjuk hozzá. A GRÁF-BŐVÍTÉS ezek után mutex kapcsolatokat keres, és hozzáadja ezeket a gráfhoz.

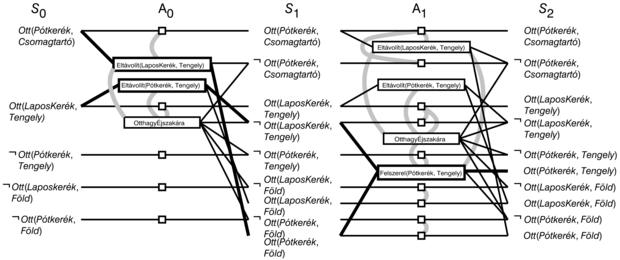
11.14. ábra - A kerékcsere probléma tervkészítési gráfja az S2 szintre bővítés után. A mutex kapcsolatokat szürke vonalak jelölik. Csak néhány fontos mutexet mutatunk, mert az ábra olvashatatlanná válna, ha az összeset jelölnénk. A megoldást megvastagított vonalak és kiemelések jelölik.
A kerékcsere probléma tervkészítési gráfja az S2 szintre bővítés után. A mutex kapcsolatokat szürke vonalak jelölik. Csak néhány fontos mutexet mutatunk, mert az ábra olvashatatlanná válna, ha az összeset jelölnénk. A megoldást megvastagított vonalak és kiemelések jelölik.

Az Ott(Pótkerék, Tengely) cselekvés még mindig nincs jelen az S1 állapotban, ezért most sem hívjuk meg a MEGOLDÁS-KINYERÉS lépést. A GRÁF-BŐVÍTÉS hívással a 11.14. ábrán látható tervkészítési gráfot kapjuk. Most, hogy a cselekvések teljes skálája rendelkezésre áll, ideje néhány példát nézni a mutex kapcsolatokra és a hatásaikra:

  • Nem konzisztens hatások: az Eltávolít(Pótkerék, Csomagtartó) mutex kapcsolatban van az OtthagyÉjszakára cselekvéssel, mert az egyik következménye az Ott(Pótkerék, Föld), míg a másiké ennek negáltja.

  • Interferencia: az Eltávolít(Pótkerék, Tengely) mutex az OtthagyÉjszakára cselekvéssel, mert az egyiknek előfeltétele az Ott(Laposkerék, Tengely), míg a másiknak ennek negáltja a következménye.

  • Versenyhelyzet: a Felszerel(Pótkerék, Tengely) mutex az Eltávolít(Laposkerék, Tengely) cselekvéssel, mert az egyiknek előfeltétele az Ott(Laposkerék, Tengely), míg a másiké ennek negáltja.

  • Inkonzisztens tartó: az Ott(Pótkerék, Tengely) és az Ott(Laposkerék, Tengely) kölcsönösen kizáróak az S2-ben, mert az Ott(Pótkerék, Tengely) csak a Felszerel(Pótkerék, Tengely) cselekvéssel érhető el, ami mutex a megőrző cselekvéssel, mely az Ott(Laposkerék, Tengely) egyetlen elérése. A mutex kapcsolatok így azonnal érzékelik a konfliktust, ami abból adódik, hogy két objektumot ugyanazon időpontban azonos helyre próbálunk tenni.

Ez alkalommal visszamegyünk a ciklus kezdetére. A cél minden literálja jelen van S2-ben, és egyik sem áll kölcsönös kizárásban egyetlen másikkal sem. Ez azt jelenti, hogy egy megoldás létezhet, és a MEGOLDÁS-KINYERÉSmegtalálhatja. Lényegében a MEGOLDÁS-KINYERÉS egy kétértékű kényszerkielégítési problémát old meg, melynek változói a szintek cselekvései, és az értékeik pedig azt jelzik, hogy benne vannak-e vagy nincsenek benne a tervben. Ehhez egy egyszerű kényszerkielégítési algoritmust használhatunk, vagy definiálhatjuk a MEGOLDÁS-KINYERÉS-t mint egy keresési problémát. Itt a keresés minden állapota a kielégítetlen célok egy halmazát tartalmazza, valamint egy mutatót a tervkészítési gráf egy szintjére. Ezt a keresési problémát a következőképpen definiáljuk:

  • A kiindulási állapot a tervkészítési gráf utolsó szintje (Sn) a tervkészítési probléma céljaival egyetemben.

  • Az Si szint állapotában rendelkezésre álló cselekvések összessége, az Ai–1 cselekvéseinek azon konfliktusmentes részhalmaza, melyek következményei elérik az állapotban lévő célokat. Az eredményként előálló állapot szintje Si–1, céljai pedig a kiválasztott cselekvések előfeltételei. A „konfliktusmentességen” olyan cselekvések halmazát értjük, amelyek között nincs kettő, amelyek kölcsönösen kizárnák egymást, és az előfeltételeik között sem szerepelnek kölcsönösen kizáró párok.

  • A cél, hogy elérjünk az S0 szinten egy állapotot úgy, hogy minden cél teljesüljön.

  • Minden cselekvés költsége 1.

Ehhez a problémához az S2 szintről indulunk, az Ott(Pótkerék, Tengely) céllal. Az egyetlen választásunk, hogy elérjük ezt a célt, a Felszerel(Pótkerék, Tengely) cselekvés. Ez az S1 keresési állapothoz visz minket, melynek céljai az Ott(Pótkerék, Föld) és az ¬Ott(Laposkerék, Tengely). Az előbbit az Eltávolít(Pótkerék, Csomagtartó) cselekvéssel érhetjük el, míg a későbbit az Eltávolít(Laposkerék, Tengely) vagy az OtthagyÉjszakára cselekvések egyikével. Az OtthagyÉjszakára kölcsönösen kizáró kapcsolatban van a Eltávolít(Pótkerék, Csomagtartó)-val, ezért az egyetlen megoldás, hogy az Eltávolít(Pótkerék, Csomagtartó) és az Eltávolít(Laposkerék, Tengely) cselekvéseket választjuk. Ez az S0 keresési állapotra vezet, az Ott(Pótkerék, Csomagtartó) és az Ott(Laposkerék, Tengely) célokkal. Mindkettő jelen van az állapotban, így megvan a megoldásunk: az Eltávolít(Pótkerék, Csomagtartó) cselekvés és az Eltávolít(Laposkerék, Tengely) az A0 szinten, melyet az A1-ben a Felszerel(Pótkerék, Tengely) követ.

Tudjuk, hogy a tervkészítés polinomiális helyigényű, és hogy a tervkészítési gráf elkészítése polinomiális idejű, ezért tudjuk, hogy a megoldás kinyerése legrosszabb esetben kezelhetetlen. Ebből kifolyólag valamifajta heurisztika segítségére lesz szükségünk, hogy a cselekvések közül válasszunk a visszafelé keresés során. A gyakorlatban jól működik egy mohó algoritmus, mely a literálok között a szintköltség alapján választ. Bármely célhalmazra a következő sorrendben járunk el:

  1. Elsőként a legmagasabb szintköltségű literált választjuk.

  2. Hogy teljesítsük ezt a literált, válasszuk először a legegyszerűbb előfeltételekkel rendelkező cselekvést, azaz válasszuk azt az akciót, melynek előfeltételeire a szintköltségek összege (vagy maximuma) a legkisebb!

11.4.3. A Graphplan algoritmus leállása

Eddig átsiklottunk a leállás kérdése fölött. Lehetünk-e biztosak abban, hogy amennyiben egy problémának nincs megoldása, a GRAPHPLAN algoritmus nem kerül végtelen ciklusba, iterációnként bővítve a tervkészítési gráfot? A válasz igen, de ennek bizonyítása túlmutat ennek a könyvnek a keretein. Itt csak a fő ötleteket körvonalazzuk, különösen azokat, melyek a tervkészítési gráfok általános tulajdonságaira világítanak rá.

Az első lépés, hogy észrevegyük, hogy a tervkészítési gráfok bizonyos tulajdonságai monoton növekvők vagy csökkenők. „X monoton növekvő” azt jelenti, hogy az X-ek halmaza az i-edik szinten az i + 1-edik szint halmazának (nem feltétlenül valódi) részhalmaza. A tulajdonságok a következők:

  • Monoton növekvő literálok. Ha egy literál megjelenik egy adott szinten, akkor az ezt követő összes szinten megjelenik. Ez a megőrző cselekvések miatt van, azaz, ha egy literál megjelenik, a megőrző cselekvések hatására örökké megmarad.

  • Monoton növekvő cselekvések. Ha egy cselekvés megjelenik egy adott szinten, akkor az ezt követő összes szinten megjelenik. Ez a literálok növekedésének a következménye, azaz, ha egy cselekvés előfeltételei megjelennek egy szinten, akkor az összes ezt követő szinten rendelkezésre állnak, így a cselekvés is.

  • A kölcsönös kizárások monoton csökkenése. Ha két cselekvés kölcsönösen kizárja egymást az Ai szinten, akkor az összes ezt megelőző szinten, ahol mindketten megjelennek, szintén kölcsönösen kizárják egymást. Ugyanez igaz a literálok közötti kölcsönös kizárásokra. Ez az ábrákon nem mindig látható, mert ezek a következő egyszerűsítést használják: nem ábrázolják sem azokat a literálokat, melyek egy adott Si szinten nem teljesülnek, sem azokat a cselekvéseket, amelyek egy adott Ai szinten nem végrehajthatók. Láthatjuk, hogy a kölcsönös kizárások monoton csökkenése igaz, ha figyelembe vesszük, hogy a nem látható literálok és cselekvések minden mással kölcsönösen kizárják egymást.

A bizonyítás egy kicsit összetett, de a következő esetekkel kezelhető: ha az A és B cselekvések kölcsönösen kizárják egymást az Ai szinten, akkor ezt csak a háromféle kizárás egyike okozhatja. Az első kettő – az inkonzisztens hatások, illetve a következtetések – a cselekvések tulajdonságai, így, ha a cselekvések kölcsönösen kizárják egymást az Ai szinten, akkor minden szinten kizárók lesznek. A harmadik eset a versenyhelyzet, az Si szint feltételeitől függ: ennek a szintnek tartalmaznia kell az A1 olyan előfeltételét, amely kölcsönösen kizáró a B1 előfeltétellel. Ez a két előfeltétel akkor lehet kölcsönösen kizáró, ha egymás negáltjai (amely esetben minden szinten kölcsönösen kizárók), vagy ha minden cselekvés, amely teljesíti az egyiket, kölcsönösen kizáró az összes cselekvéssel, mely a másikat érheti el. Mi már tudjuk, hogy a rendelkezésre álló cselekvések monoton növekednek, így indukcióval bizonyítható, hogy a kölcsönös kizárások csökkenők.

Mivel a cselekvések és a literálok növekednek, a kölcsönös kizárások csökkennek, és mivel csak véges számú cselekvés és literál van, minden tervkészítési gráf szükségszerűen kiegyenlítődik – azaz minden egymást követő szint azonos lesz. Ha hiányzik a probléma egy célja, vagy a célok között vannak kölcsönösen kizárók, miután a gráf kiegyenlítődött, akkor a probléma soha nem oldható meg, így leállíthatjuk a GRAPHPLAN algoritmust, és hibával térhetünk vissza. Ha a gráf kiegyenlítődik, és minden cél jelen van kizárások nélkül, de a MEGOLDÁS-KINYERÉS sikertelen a megoldás megtalálásában, akkor lehet, hogy véges lépésszámban bővítenünk kell a gráfot, de végezetül megállhatunk. A megállás problémaköre ennél összetettebb, amit itt nem tárgyalunk.

fel