1909-ben Charles Peirce egy egzisztenciális gráfoknak (existential graphs) elnevezett grafikus jelölésrendszert javasolt, ami az ő elnevezése szerint a „jövő logikája”. Ezzel kezdetét vette a „logika” és a „szemantikus hálók” szószólóinak hosszú vitája. Sajnos a vita elfedte azt a tényt, hogy a szemantikus hálók – legalább a jól definiált szemantikával ellátottak – a logika egy formáját jelentik. Bizonyosfajta állítások számára a szemantikus hálók nyújtotta jelölés gyakran kényelmesebb, azonban ha az „emberi interfész” problémáktól eltekintünk, a mögötte felsorakozó fogalmak – az objektumok, a relációk, a kvantifikálás stb. – mind ugyanazok.

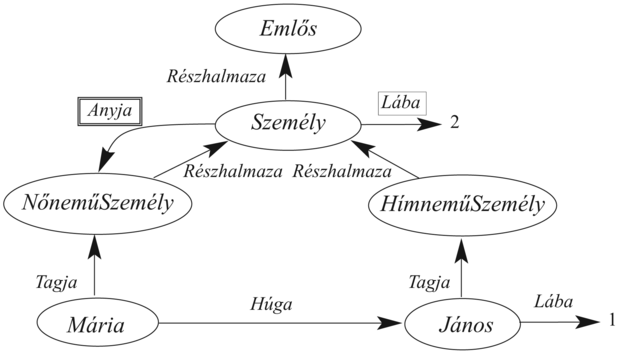
A szemantikus hálóknak több változata van, mindegyik képes azonban az egyedi objektumokat, az objektumok kategóriáit és az objektumok közötti relációkat reprezentálni. A tipikus grafikus jelölés objektumok, illetve kategóriák neveit ovális keretekben vagy dobozokban mutatja, címkézett élekkel összekapcsolva. A 10.9. ábrán például a Mária és a NőneműSzemély között Tagja kapcsolat van, ami annak a logikai állításnak felel meg, hogy Mária ∈ NőneműSzemély. Hasonlóan a Mária és a János közötti Húga kapcsolat annak az állításnak felel meg, hogy Húga(Mária, János). A kategóriákat a Részhalmaza éllel kapcsolhatjuk össze. A krumplik és a nyilak rajzolása annyira szórakoztató, hogy könnyű kísértésbe esni. Tudjuk például, hogy minden személy anyja egy nőnemű személy, szabad-e akkor a Személy-től a NőneműSzemély-ig egy Anyja élt húzni? A válasz nem, merthogy az Anyja egy reláció egy személy és az anyja között, a kategóriáknak viszont nincsen anyjuk.^[101] Emiatt a kapcsolatra a 10.9. ábrán egy külön jelölést használtunk – egy kettős vonallal történő bekeretezést. Ez a kapcsolat azt állítja, hogy:

∀x x ∈ Személy ⇒ [∀y Anyja(x, y) ⇒ y ∈ NőneműSzemély]

Esetleg azt is állíthatnánk, hogy egy személynek két lába van, azaz:

∀x x ∈ Személy ⇒ Lába(x, 2)

Mint korábban, most is óvatosnak kell lennünk, nehogy azt állítsuk, hogy kategóriának van két lába. A 10.9. ábra egyszeres vonallal végzett keretezése jelzi az egy kategória minden tagjának tulajdonságaira vonatkozó állítást.

A szemantikus háló jelölésrendszere igen alkalmas a 10.2. alfejezetben bevezetett típusú öröklődéses (inheritance) következtetés végrehajtására. Így személy révén, Mária örökli azt a tulajdonságot, hogy két lába van. Ahhoz, hogy kitaláljuk, hány lába van Máriának, az öröklődéses algoritmus követi a Tagja élt a Máriá-tól az őt tartalmazó kategóriáig, majd a Részhalmaza élt a hierarchiába felfelé, amíg egy olyan kategóriát nem talál meg, amelyhez létezik egy bekeretezett Lába él – ebben ez esetben ez Személy kategória lesz. Ennek az öröklődéses algoritmusnak az egyszerűsége és hatékonysága a logikai tételbizonyítóhoz képest, a szemantikus hálók egyik fő vonzereje volt.

Az öröklődés komplikálódik, amikor egy objektum egyszerre több kategóriához tartozhat, vagy pedig amikor egy kategória több kategória részhalmaza. Ezt az esetet többszörös öröklődésnek (multiple inheritance) nevezzük. Az ilyen helyzetben a öröklődéses algoritmus esetleg két vagy több, egymással ellentétes választ talál a felkérésre. Ennél fogva a többszörös öröklődés bizonyos objektumorientált programozási (object-oriented programming, OOP) nyelvekből, mint amilyen például a Java, ami az osztályhierarchiában öröklődést használ, ki van zárva. Szemantikus hálókban a többszörös öröklődést általában megengedjük, de ennek részletes tárgyalását a 10.7. alfejezetre hagyjuk.

A következtetés másik közönséges formája az inverz kapcsolatok (inverse links) használata. Például a VanHúga a Húga inverze, azaz:

∀p, s VanHúga(p, s) ⇔ Húga(s, p)

Ezt az állítást megfogalmazhatjuk szemantikus hálóval, feltéve hogy a kapcsolatok reifikáltak (reified), azaz önálló objektumnak tekinthetők. Így például VanHúga objektumot az Inverze éllel lehetne összekapcsolni a Húga objektummal. Ha egy lekérdezés azt firtatná, hogy ki Jánosnak a Húga, az öröklődéses algoritmus felfedezheti, hogy a VanHúga a Húga inverze, és a lekérdezést úgy megválaszolhatja, hogy a VanHúga kapcsolatot János-tól Máriá-ig követi végig. Az inverz információ nélkül esetleg szükséges lehetne az összes nőnemű személyt megvizsgálni, van-e netán Húga kapcsolata Jánossal. Ez amiatt van így, mert a szemantikus háló közvetlen indexelést csak az objektumok, a kategóriák és a belőlük induló kapcsolatok esetén biztosít. Az elsőrendű logika nyelvében ez annak felel meg, mintha a tudásbázist a predikátumok csakis első argumentumai szerint indexelnénk.

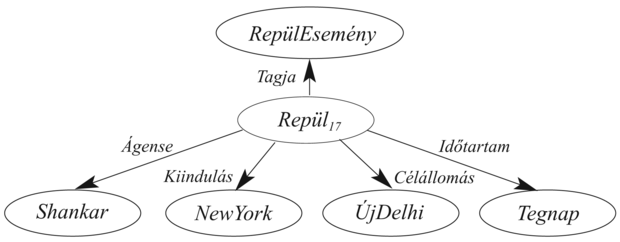
Az olvasó talán felfedezte már a szemantikus háló jelölésnek egy nyilvánvaló hátrányát az elsőrendű logikához képest. A krumplik közötti élek csak bináris relációkat reprezentálnak. A Repül(Shankar, NewYork, Újdelhi, Tegnap) állítást a hálóban közvetlenül megfogalmazni nem tudjuk. Az n értékű állítások hatását megkaphatjuk azonban, ha az állítást magát egy, az események megfelelő kategóriájához tartozó eseményként reifikáljuk (lásd 10.3. alfejezet). A 10.10. ábra ehhez a konkrét eseményhez tartozó szemantikus hálóstruktúrát mutat. Jegyezzük meg, hogy a bináris relációkra vonatkozó korlátozás a reifikált fogalmak gazdag ontológiáját teszi szükségessé. Az ebben a fejezetben kifejlesztett ontológia zöme ténylegesen a szemantikus hálós rendszerekben gyökerezik.

Állítások reifikálása lehetővé teszi, hogy az elsőrendű logika minden rögzített, függvénymentes atomi állítása reprezentálható szemantikus hálós jelöléssel. Univerzálisan kvantifikált állítások bizonyos típusai reprezentálhatók a kategóriákra alkalmazott inverz kapcsolatok, valamint egyszeresen és kétszeresen bekeretezett élek alkalmazásával, ettől még persze az elsőrendű logikától messze vagyunk. A negálás, a diszjunkció, a beágyazott függvényszimbólumok és az egzisztenciális kvantifikálás mind hiányzik. Manapság lehetséges a jelölés kiterjesztése, hogy az az elsőrendű logikával ekvivalens legyen – ilyenek például a Pierce-féle egzisztenciális gráfok vagy Hendrix-féle particionált szemantikus hálók (Hendrix, 1975) – ez viszont a szemantikus hálók fő előnyét – az öröklődéses folyamat egyszerűségét és átláthatóságát – semmisíti meg. A tervezők nagy hálókat építhetnek, és még mindig lehetnek jó ötleteik, hogy mely lekérdezések lesznek hatékonyak, mert (a) az öröklődéses eljárás lépéseit könnyű vizualizálni, (b) egyes esetekben a lekérdezés nyelve olyan egyszerű, hogy bonyolult lekérdezéseket feltenni nem is lehet. Azokban az esetekben, amikor a kifejezőerő túlságosan korlátozott, számos szemantikus hálórendszer a procedurális kiegészítéshez (procedural attachment) folyamodik, hogy a hiányokat kitöltse. A procedurális kiegészítés egy olyan módszer, amikor egy bizonyos relációra vonatkozó lekérdezés (néha állítás) egy, a relációhoz megtervezett speciális eljárás, és nem egy általános öröklődéses algoritmus meghívását eredményezi.

A szemantikus hálók egyik legfontosabb aspektusa, hogy képesek a kategóriák számára az alapértelmezett értékeket (default values) reprezentálni. A 10.9. ábra gondos végignézésével észrevehetjük, hogy Jánosnak egy lába van annak ellenére, hogy ő egy személy, és minden személynek két lába van. Egy tisztán logikai tudásbázisban ez egy ellentmondás lenne, de a szemantikus hálóban az az állítás, hogy minden személynek két lába van, egy alapeseti állítás, azaz egy személyről feltételezzük, hogy két lába van, ha nincs ezzel ellentmondó specifikusabb információ. Az alapeseti szemantikát természetesen az öröklődéses következtetés kényszeríti ki, mert a kapcsolatokat magától az objektumtól (itt Jánostól) felfelé követi, és megáll, hacsak egy értéket meg nem talál. Azt mondjuk, hogy az alapeseti értéket egy specifikusabb érték felülírhatja (overridden). Vegyük észre, hogy lábak számát felül tudnánk írni egy EgyLábúSzemély kategória létesítésével, ami a Személy Részhalmaza lenne, és amelynek János lenne a tagja.

A háló szigorúan logikai szemantikáját megtarthatjuk, ha azt mondjuk, hogy a Lába állítás a Jánosra vonatkozó kivételt tartalmazza:

∀x x ∈ Személy ∧ x ≠ János ⇒ Lába(x, 2)

Egy rögzített háló esetén ez szemantikusan megfelelő, azonban ha sok kivételünk lesz, kevésbé tömör lesz a felírásunk, mint a hálós jelölés maga. Több állítással frissített háló esetén az ilyen megközelítés sajnos kudarcra van ítélve – amit valójában mondani szeretnénk az az, hogy minden, egyelőre még ismeretlen egylábú személy szintén kivételnek számít. Ezzel a témával és az alapeseti következtetéssel általában bővebben a 10.7. alfejezet foglalkozik.

Az elsőrendű logika szintaxisát úgy tervezték, hogy egyszerű legyen objektumokról kijelentéseket tenni. A leíró logikák (description logics) olyan jelölések, amelyeket a kategóriák definícióinak és tulajdonságainak könnyebb leírására terveztek. A leíró logikák a szemantikus hálókból alakultak ki, válaszul arra a nyomásra, hogy a hálók jelentését formalizáljuk, hangsúlyozva emellett a taxonómia szervezési elvként való használatát.

A leíró logika alapvető következtetési feladata a részvizsgálat (subsumption) – annak ellenőrzése, hogy egy kategória része-e egy másiknak a definícióik alapján – és az osztályozás (classification) – annak ellenőrzése, hogy egy objektum egy kategóriába tartozik-e. Bizonyos rendszerek egy kategóriadefiníció konzisztenciavizsgálatát (consistency) is tartalmazzák arra, hogy a tagsági kritérium logikailag kielégíthető-e.

A CLASSIC nyelv (Borgida és társai, 1989) egy tipikus leíró logika. A 10.11. ábra mutatja a CLASSIC leírások szintaxisát (az érthetőség kedvéért a nyelv kulcsszavait magyar fordításban adjuk meg – a ford.).^[102] Azt az állítást például, hogy az agglegények nőtlen, felnőtt férfiak, következőképpen írhatnánk le:

Agglegény = És(Nőtlen, Felnőtt, Férfi)

Ennek elsőrendű logikai ekvivalense a következő lenne:

Agglegény(x) ⇔ Nőtlen(x) ∧ Felnőtt(x) ∧ Férfi(x)

Vegyük észre, hogy a leíró logika hatékonyan teszi lehetővé azt, hogy a predikátumokon direkt logikai műveleteket hajtsunk végre anélkül, hogy először mondatokat alkotnánk, amiket azután összekapcsolunk kötőszavakkal. Bármilyen leírás a CLASSIC-ban kifejezhető elsőrendű logikával, de bizonyos leírások a CLASSIC-ban sokkal világosabbak. Például az emberek egy olyan halmazának leírásához, akiknek legalább három fiuk van, és a fiúk mind munkanélküliek, és a feleségeik orvosok, valamint maximum két lányuk van, akik vagy fizika, vagy matematika tanszéken professzorok, azt használnánk, hogy:

És(Férfi, Legalább(3, Fiú), Legfeljebb(2, Lány),

Mind(Fiú, És(Munkanélküli, Házas, Mind(Feleség, Orvos))),

Mind(Lány, És(Professzor, Betölt(Tanszék, Fizika, Matematika))))

Gyakorlatként meghagyjuk ennek lefordítását elsőrendű logikára.

A leíró logikák talán egyik legfontosabb aspektusa a következtetés nyomon követhetőségére tett hangsúly. Egy problémaeset megoldása a leírásával kezdődik, majd annak megkérdezésével folytatódik, hogy része-e a lehetséges megoldás a kategóriák egyikének. Standard elsőrendű logikában a válasz idejének megjóslása gyakran lehetetlen. Gyakran a felhasználóra vár a reprezentáció olyan átalakítása, hogy kikerülje azokat a mondathalmazokat, amelyek miatt úgy tűnik, hogy a rendszernek több hétbe telik a probléma megoldása. A leíró logikák viszont azt biztosítják, hogy a részvizsgálat megoldható legyen polinomiális idő alatt a probléma leírásától függően.^[103]

Ez a gyakorlatban csodálatosan hangzik, míg az ember rá nem jön, hogy a következő két konzekvencia valamelyike lehetséges csak: a nehéz problémákat vagy nem lehet kifejezni, vagy exponenciálisan nagy leírást igényelnek! Mindenesetre a kezelhetőség eredményei vetnek némi fényt arra, hogy milyen konstrukciók okoznak bajt, és így segítik a felhasználót annak megértésében, hogyan viselkednek különböző reprezentációk. Például a leíró logikákból általában hiányzik a negálás és a diszjunkció. Ezek mindketten arra kényszerítik az elsőrendű logikai rendszert, hogy lényegében egy exponenciális eset analízisen menjen keresztül a teljesség biztosítása érdekében. A negálás és a diszjunkció ugyanezen ok miatt van kizárva a Prolog nyelvből is. A CLASSIC csak egy korlátozott formájú diszjunkciót engedélyez a Kitölt és az EgyBelőle szerkezetekben, ami lehetővé tesz diszjunkciót explicit módon megszámolt egyedek felett, de nem a leírások felett. Diszjunktív leírással az egymásba ágyazott definíciók könnyen exponenciális számú alternatív úthoz vezethetnek, amelyekben az egyik kategória könnyen része lehet egy másiknak.