10.3. Cselekvések, szituációk és események
A cselekvések eredményeiről következtetni kulcsfontosságú egy tudásalapú ágens számára. A 7. fejezetben példákat láttuk olyan ítéletállításokra, amelyek leírják, hogy a cselekvések hogyan hatnak a wumpus világra. A 7.7.2. szakasz - A hely és az irány nyomkövetése részben lévő (7.3) egyenlet azt állítja például, hogy az ágens lokációja hogyan változik az ágens mozgásával. Az ítéletkalkulus egyik hátránya, hogy cselekvés leírásáról külön másolatokkal kell rendelkeznünk azokra az időpontokra, amikor a cselekvést végre fogják hajtani. Ebben az alfejezetben leírt, az elsőrendű logikára alapozó reprezentációs módszer ezt a problémát elkerüli.
Az axiómák többszörös másolatainak az elkerülésére nyilvánvaló módszer az idő szerinti kvantifikálás – azaz azt mondani, hogy „∀t-re a t-beli cselekvésnek ez a t + 1-beli eredménye”. A t + 1 típusú explicit időpillanatok helyett ebben az alfejezetben szituációkkal dolgozunk, amelyek a cselekvések végrehajtásából adódó állapotok jelölései. E megközelítés neve szituációkalkulus (situation calculus) és az alábbi ontológiára támaszkodik:
-
A 8. fejezethez hasonlóan a cselekvések logikai termek, például az Előre, a Fordulj(Jobbra). Egyelőre feltételezzük, hogy a környezetben csakis egy ágens tartózkodik. (Ha több lenne, egy további argumentummal megjelölhetjük, hogy melyik ágens hajtja végre a cselekvést).
-
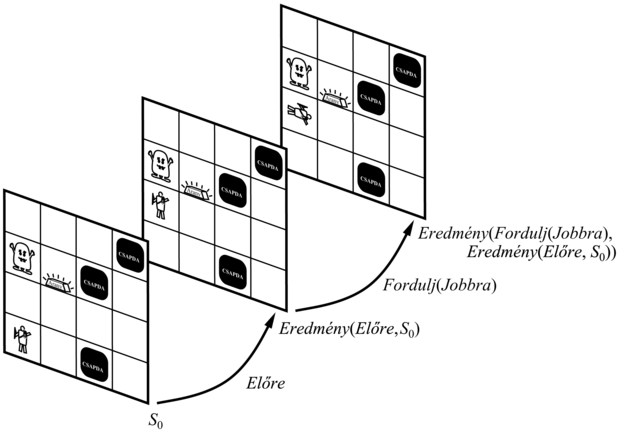
A szituációk (situations) logikai termek, amelyekhez tartozik egy (általában S0-nak jelölt) kezdeti szituáció és minden más szituáció, amely a szituációra vonatkozó cselekvés végrehajtásából adódott. Ha az a cselekvést az s szituációban hajtották végre, az eredményezett szituációt Eredmény(a, s) (néha Csináld-nak nevezett) függvény nevezi meg. A gondolatot a 10.2. ábra illusztrálja.
-
A folyó események (fluents) olyan függvények és predikátumok, amelyek szituációról szituációra változnak. Ilyen például az ágens lokációja vagy a wumpus jóléte. A szótár szerint a folyó valamilyen folyadékszerű viselkedésre utal. Használatunkban a szituációk menti lefolyását vagy változását jelenti. ¬Tart(G1, S0) például azt mondja, hogy az ágens a kezdeti S0 szituációban a G1 aranyat nem tartja a kezében. Kor(Wumpus, S0) a wumpus S0-beli életkorára vonatkozik.
-
Engedélyezzük az időtlen, örök (atemporal, eternal) predikátumokat és függvényeket is. Példaként tekinthetjük az Arany(G1) vagy a BalLába(Wumpus) predikátumokat.
Az egyedi cselekvéseken túlmenően hasznos, ha a cselekvések sorozatairól is tudunk következtetni. A sorozat eredményét az egyedi cselekvések eredménye alapján definiálhatjuk. Először azt fogjuk mondani, hogy egy üres sorozat végrehajtása a szituációt változatlanul meghagyja:
Eredmény([], s) = s
Egy nem üres sorozat végrehajtása nem más, mint az első cselekvés végrehajtása, majd az eredményül adódó szituációban a maradó sorozatnak a végrehajtása:
Eredmény([a]sorozat, s) = Eredmény(sorozat, Eredmény(a, s))
Egy szituációkalkulus ágensnek tudnia kellene egy adott cselekvéssorozat eredményét kikövetkeztetni, ez az ún. előrevetítő feladat (projection task). A megfelelő konstruktív következtetési mechanizmus birtokában képesnek kellene lennie arra is, hogy egy kívánatos eredményt biztosító sorozatot megtaláljon, ez az ún. tervkészítési feladat (planning task).
Egy módosított wumpus világról fogunk példát venni, ahol az ágens orientációjával nem törődünk, és ahol az ágens egy helyről egy szomszédos helyre Megy. Tegyük fel, hogy ágens az [1, 1]-nél és arany az [1, 2]-nél van. A cél az aranyat az [1,1] helyen birtokoljuk. A folyó esemény predikátumok a Nála(o, x, s) és Tart(o, s). A kezdeti tudásbázis az alábbi leírást tartalmazhatná:
Nála(Ágens, [1, 1], S0) ∧ Nála(G1, [1, 2], S0)
Ez azonban még nem elég, mert nem mondtuk, hogy az S0-ban mi nem igaz (a probléma további elemzését lásd a 10.7. szakasz - Következtetés alapértelmezett információval részben). A teljes leírás az alábbi:
Nála(o, x, S0) ⇔ ∧ [(o = Ágens ∧ x = [1, 1]) ∨ (o = G1 ∧ x = [1, 2])]
¬Tart(o, S0)
Arra is szükség van, hogy kijelentsük, G1 egy arany, és [1, 1] és [1, 2] szomszédosak:
Arany(G1) ∧ Szomszédos([1, 1], [1, 2]) ∧ Szomszédos([1, 2], [1, 1])
Valaki bizonyára azt szeretné bebizonyítani, hogy ágens a célját eléri, ha az [1, 2]-re átmegy, ott megfogja az aranyat és az [1, 1]-re visszatér, azaz:
Nála(G1, [1, 1], Eredmény([Megy([1, 1], [1, 2]), Megfog(G1), Megy([1, 2], [1, 1])], S0)
Annál érdekesebb lehetőség az arany birtoklását biztosító tervet készíteni, amit a „milyen cselekvéssorozat eredménye az arany az [1, 1]-en?” kérdés megválaszolásával lehet megtenni.
∃sorozat Nála(G1, [1, 1], Eredmény(sorozat, S0))
Nézzük, hogy e kérdések megválaszolásához mivel kellene a tudásbázist kiegészíteni.
A szituációkalkulus legegyszerűbb változatában minden cselekvést két axiómával lehet leírni. A lehetőségi axióma (possibility axiom) megmondja, hogy a cselekvést mikor lehet elvégezni, a hatásaxióma (effect axiom) pedig azt, hogy a cselekvés végrehajtásával mi is fog történni. Annak jelölésére, hogy az s szituációban az a cselekvés végrehajtása lehetséges, a Lehet(a, s) predikátumot fogjuk használni. Az axiómák formája az alábbi:
Lehetőségi Axióma: Előfeltételek ⇒ Lehet(a, s)
Hatásaxióma: Lehet(a, s) ⇒ A cselekvés végrehajtásából adódó változások
Ezeket az axiómákat a módosított wumpus világra fogjuk felírni. A mondatok rövidsége érdekében el fogjuk hagyni az egész mondatra vonatkozó univerzális kvantorokat. Feltételezzük, hogy az s változó a szituációkra, az a változó a cselekvésekre, az o változó az objektumokra (az ágenseket beleértve), a g változó az aranyra, az x és az y változók pedig a helyre vonatkoznak.
Az erre a világra vonatkozó lehetőségi axióma azt mondja, hogy egy ágens a szomszédos helyek között mozoghat, az aktuális helyen megfoghatja az aranyat és elengedheti az aranyat, amelyet tartott:
Nála(Ágens, x, s) ∧ Szomszédos(x, y) ⇒ Lehet(Megy(x, y), s)
Arany(g) ∧ Nála(Ágens, x, s) ∧ Nála(g, x, s) ⇒ Lehet(Megfog(g), s)
Tart(g, s) ⇒ Lehet(Elenged(g), s)
A hatásaxióma azt állítja, hogy ha egy cselekvés lehetséges, akkor a cselekvés végrehajtásából adódó szituációban bizonyos tulajdonságok (folyó események) érvényesek lesznek. Az x-ről az y-ra menni cselekvés eredménye az y-ban tartózkodni, az aranyat megfogni eredménye az aranyat tartani, végül az aranyat elengedni eredménye az aranyat nem tartani:
Lehet(Megy(x, y), s) ⇒ Nála(Ágens, y, Eredmény(Megy(x, y), s))
Lehet(Megfog(g), s) ⇒ Tart(g, Eredmény(Megfog(g), s))
Lehet(Elenged(g), s) ⇒ ¬Tart(g, Eredmény(Elenged(g), s))
Az axiómák megállapításával tudjuk-e bizonyítani, hogy a tervünk biztosítja a cél elérését? Sajnos még nem! Először minden jól működik: a Megy([1, 1], [1, 2]) valójában lehetséges az S0-ban, és a Megy hatásaxiómája meggyőzhet minket, hogy az ágens tényleg eléri az [1, 2]-t:
Nála(Ágens, [1, 2], Eredmény(Megy([1, 1], [1, 1 ]), S0))
Most tekintsük a Megfog(G1) cselekvést. Ki kell mutatni, hogy ez lehetséges az új szituációban, azaz:
Nála(G1, [1, 2], Eredmény(Megy([1, 1], [1, 2]), S0))
Fontos
Sajnos a tudásbázisunkban az ilyen konklúziót semmi sem támasztja alá. Intuitíve persze megértjük, hogy az ágens Megy cselekvése az arany helyzetére nincs hatással, így az még mindig az [1, 2]-ben van, ahogy ott volt az S0 szituációban is. A probléma az, hogy a hatásaxióma kijelenti, hogy mi változik, de nem mond semmit arról, hogy mi nem változik.
A változatlanul megmaradó dolgok reprezentálása az ún. keretprobléma (frame problem). A keretproblémára hatékony megoldást kell találnunk, mert a valódi világban az idő többségében majdnem minden változatlan marad. Minden egyes cselekvés a folyó eseményeknek csak kis töredékét befolyásolja.
Az egyik megközelítés az expblicit keretaxiómák (frame axioms) felírása, amelyek azt mondják, hogy mi marad változatlan. Az ágens mozgásai például más objektumok helyzetét változatlanul hagyják, hacsak azokat az ágens nem tartja magánál:
Nála(o, x, s) ∧ (o ≠ Ágens) ∧ ¬Tart(o, s) ⇒ Nála(o, x, Eredmény(Megy(y, z), s))
Ha összesen F folyó esemény és A cselekvés lenne, akkor O(AF) keretaxiómára lenne szükségünk. Másfelől, ha minden cselekvésnek legfeljebb E hatása lenne, ahol az E tipikusan jóval kisebb, mint F, akkor a történteket sokkal kisebb, O(AE) nagyságú tudásbázissal is ki tudnánk fejezni. Ez a reprezentációs keretprobléma (representational frame problem). A vele szorosan kapcsolódó következtetési keretprobléma (inferential frame problem) egy t-lépéses cselekvéssorozat eredményeinek O(Et) időben, és nem O(Ft) vagy O(AEt) időben való kivetítése. Sorban egymás után az összes problémával fogunk foglalkozni. Azonban egy probléma mégis marad – biztosítani, hogy egy cselekvés sikeres elvégzéséhez minden feltételt sikerült megfogalmazni. Így például a Megy kudarccal fenyeget, ha az ágens útközben meghal. Ez az ún. kvalifikációs probléma (qualification problem), melynek teljes megoldása nincs.
A reprezentációs probléma megoldása csak egy kis változást igényel abban, hogy az axiómákat hogyan írjuk fel. Ahelyett hogy felírnánk minden cselekvés hatását, azzal foglalkozunk inkább, hogy egy folyó esemény időben hogyan evolvál.[96] Az általunk használt axiómákat követő állapot axiómáknak (successor-state axioms) hívják. Alakjuk a következő:
Követő-Állapot Axióma:
Cselekvés lehetséges ⇒
(Folyó esemény igaz az eredmény állapotban ⇔ A cselekvés hatása igazzá tette
∨ Igaz volt a cselekvés előtt és a cselekvés nem változtatta)
Feltételezve, hogy lehetetlen cselekvésekkel nem foglalkozunk, vegyük észre, hogy a definícióban ⇔ szerepel ⇒ helyett. Ez azt jelenti, hogy a folyó esemény akkor és csak akkor lesz igaz, ha a jobb oldali rész igaz. Más szóval minden folyó eseménynek a következő állapotban érvényes igazságértékét a cselekvésnek és az aktuális állapotban érvényes értékének a függvényeként határozzuk meg. Ez azt jelenti, hogy a következő állapot teljesen meghatározott az aktuális állapottól kiindulva, és így pótlagos keretaxiómákra nincs szükség.
Az ágens helyére érvényes követő állapot axióma azt mondja, hogy ágens egy cselekvés után az y-ban lesz, ha a cselekvés lehetséges, és az az y-ba való mozgásból áll, vagy ha az ágens már az y-ban tartózkodott, és a cselekvésnek a mozgáshoz nem volt köze:
Lehet(a, s) ⇒
(Nála(Ágens, y, Eredmény(a, s)) ⇔ (a = Megy(x, y))
∨ (Nála(Ágens, y, s) ∧ (a ≠ Megy(y, z)))
A Tart axiómája azt fejezi ki, hogy ágens tarja a g-t, ha a cselekvés a g megfogását jelentette, és a cselekvés lehetséges volt, vagy ha az ágens már tartotta a g-t és a cselekvés nem annak elengedése volt:
Lehet(a, s) ⇒
(Tart(g, Eredmény(a, s)) ⇔ (a = Megfog(g)) ∨ (Tart(g, s) ∧ (a ≠ Elenged(g)))
Fontos
A követő állapot axiómák a reprezentációs keretproblémát megoldják, mert az axiómák össz-száma O(AE) literál. Az E hatások és az A cselekvések mindegyike pontosan egyszer kerül említésre. A literálok F különböző axióma között vannak szétosztva, így egy axióma átlagos nagysága AE/F.
Az éles szemű olvasó észreveszi, hogy ezek az axiómák a Nála folyó eseményt kezelik az ágens számára, de nem így az arany esetében. Még mindig nem tudjuk bebizonyítani, hogy ez a háromlépéses terv eljut a célhoz, az arany eléréséhez az [1, 1]-ben. Amire szükségünk lenne még, az annak a kijelentése, hogy az ágens x-től y-ig való mozgásának implicit hatása (implicit effect), hogy minden, általa megfogott arany is vele fog mozogni (ahogy az aranyon a hangya, a hangyán a bacilus stb.). Az implicit hatások kezelését ramifikációs problémának (ramification problem) nevezzük. A problémát általánosságban később vitatjuk meg. A jelenlegi speciális tárgyterületen e probléma a Nála számára kissé általánosabb követő állapot axiómák felírásával megoldható. Az új axiómák, amelyek a régieket magukban foglalják, azt fejezik ki, hogy minden o objektum y-ban tartózkodik, ha az ágens az y-ba ment, és az o maga az ágens, vagy bármi, amit az ágens tart; vagy ha az o már az y-ban volt, és az ágens nem ment sehová, miközben az o maga az ágens, vagy bármi, amit az ágens tart.
Lehet(a, s) ⇒
Nála(o, y, Eredmény(a, s)) ⇔ (a = Megy(x, y) ∧ (o = Ágens ∨ Tart(o, s)))
∨ (Nála(o, y, s) ∧ ¬(∃z y ≠ z ∧ a = Megy(y, z) ∧
(o = Ágens ∨ Tart(o, s))))
Egy további technikai nehézséggel számolnunk kell. Az ilyen axiómákat felhasználó következtetési eljárásnak képesnek kell lennie az azonosság hiányát kimutatni.A legegyszerűbb eset a két konstans esete, például Ágens ≠ G1. Az elsőrendű logika általános szemantikája lehetővé teszi, hogy a különböző konstansok ugyanazt az objektumot jelentsék, a tudásbázisnak tartalmaznia kell tehát az ilyen eseteket kitiltó axiómát. Az egyedi elnevezések axiómája (unique names axiom) a konstansok azonossághiányát fejezi ki, a tudásbázisban létező minden konstanspárra. Ha a tételbizonyító rendszer az azonossághiányt feltételezi, ahelyett hogy explicit módon a tudásbázisban ez le lenne írva, az egyedi elnevezések feltételezésről (unique names assumption) beszélünk. Az azonossághiányát ki kell jelentenünk a cselekvésekre is: a Megy([1, 1], [1, 2]) cselekvés és a Megy([1, 2], [1, 1]), vagy a Megfog(G1) cselekvés nem ugyanaz. Először azt fogjuk mondani, hogy a cselekvések minden típusa különböző – semmilyen Megy cselekvés nem lehet egy Megfog cselekvés. A cselekvésnevek minden párjára:
A(x1, …, xm) ≠ B(y1, …, yn)
Most kijelentjük, hogy két, ugyanahhoz a cselekvéshez tartozó cselekvésterm ugyanazt a cselekvést jelenti, ha a benne szereplő objektumok mind azonosak:
A(x1, …, xm) = B(y1, …, ym) ⇔ x1 = y1 ∧ … ∧ xm = ym
Ezeket az állításokat együttesen egyedi cselekvés axiómáknak (unique action axioms) nevezzük. A kezdeti állapotleírás, a követő állapot axiómák, az egyedi elnevezések axiómák és az egyedi cselekvésaxiómák együttese elegendő annak bizonyításához, hogy a javasolt terv megvalósítja a célt.
Követő állapot axiómák a reprezentációs keretproblémát ugyan megoldják, de a következtetési keretproblémát nem. Tekintsünk egy olyan t-lépésű p tervet, hogy St = Eredmény(p, S0). Hogy eldönthessük, mely folyó esemény igaz St-ben, szükséges minden egyes F keretaxiómát minden t időlépésben kiértékelni. Mivel az axiómáknak átlagosan AE / F a nagyságuk, O(AEt) következtetéssel kell számolnunk. A munka zöme rá fog menni arra, hogy a folyó eseményeket az egyik szituációról a másikra változatlanul másoljuk át.
A következtetési keretprobléma megoldására két lehetőségünk van. Először is, eldobhatjuk a szituációkalkulust, és kitalálhatjuk az axiómák egészen új felírási módját. Ez történt meg az olyan formalizmusokban, mint a folyó esemény kalkulus (fluent calculus). Másodszor, megváltoztathatjuk magát a következtetési eljárást, hogy a keretaxiómákat hatékonyabban dolgozza fel. Erre utalást ad magának az egyszerű megközelítésnek az O(AEt) jellege. De miért függ ez a cselekvések A számától, amikor pontosan tudjuk, hogy mindegyik időlépésben melyik cselekvés kerül végrehajtásra? Hogy belássuk, hogyan tudnánk a dolgokon javítani, nézzük meg először a keretaxiómák formátumát:
Lehet(a, s) ⇒
Fi(Eredmény(a, s)) ⇔ (a = A1 ∨ a = A2 …)
∨ Fi(s) ∧ (a ≠ A3) ∧ (a ≠ A4) …
Vagyis mindegyik axióma említ tehát néhány cselekvést, amelyek a folyó eseményt igazzá, és néhányat, amelyek azt hamissá teszik. Ezt a körülményt formalizálhatjuk a PozHatás(a, Fi) és a NegHatás(a, Fi) predikátumok bevezetésével. A PozHatás(a, Fi) azt jelenti, hogy az a cselekvés az Fi-t igazzá, a NegHatás(a, Fi) pedig azt, hogy hamissá teszi. A fenti axióma ezzel a következőképpen írható át:
Lehet(a, s) ⇒
Fi(Eredmény(a, s)) ⇔ PozHatás(a, Fi) ∨ [Fi(s) ∧ ¬NegHatás(a, Fi)]
PozHatás(A1, Fi)
PozHatás(A2, Fi)
NegHatás(A3, Fi)
NegHatás(A4, Fi)
Az, hogy ez mennyire automatizálható, a keretaxiómák pontos formátumán múlik. Hogy az ilyen axiómákra alapozva hatékony következtetési eljárást dolgozhassunk ki, három dolgot kell még megtenni:
-
Indexeljük a PozHatás és a NegHatás predikátumokat az első argumentumaik szerint, hogy amikor adott egy t időpontban bekövetkező cselekvés, a hatásait O(1) időben meg lehessen keresni.
-
Indexeljük az axiómákat úgy, hogy amikor világos már, hogy egy cselekvés hatása Fi, O(1) idő alatt ki lehessen keresni az Fi-re vonatkozó axiómákat. Ekkor a cselekvés hatásai között nem szereplő folyó esemény axiómáival nem is kell törődni.
-
Minden szituációt reprezentáljunk egy megelőző szituáció plusz egy növekményként. Így, amikor lépésről lépésre nem változik semmi, nem kell semmiféle munkát végeznünk. A régebbi megközelítésben O(F) munka ment volna rá, hogy minden folyó esemény esetén a megelőző Fi(s) feltételezésből Fi(Eredmény(a, s)) feltételezést generáljunk.
Minden időlépésnél tehát megnézzük az aktuális cselekvést, megkeressük a hatásait és az igaz folyó események halmazát felfrissítjük. Minden időlépésben átlagosan E ilyen frissítéssel kell számolnunk, ami az eredő komplexitásra O(Et)-t ad. Ez megadja a következtetési keretprobléma megoldását.
A szituációkalkulus akkor működik jól, ha egy ágens diszkrét, azonnal lezajló cselekvéseket hajt végre. Ha cselekvéseknek időtartamuk is van, és egymással át is lapolódhatnak, a szituációkalkulus nehézkessé kezd válni. Emiatt e kérdésekkel egy más megközelítésen belül próbálkozunk, amit eseménykalkulusnak (event calculus) fogunk nevezni és amely inkább az időpontokon, mint a szituációkon alapul. (Az „esemény” és a „cselekvés” fogalmakat felváltva is használhatjuk. Egy „esemény” informálisan a cselekvések tágabb osztályát jelenti, az explicit ágenst nélkülöző cselekvéseket beleértve. Az eseményeket az eseménykalkulusban könnyebben kezelhetjük, mint a szituációkalkulusban.)
Az eseménykalkulusban a folyó események időpillanatokra és nem szituációkra vonatkoznak, és a kalkulust úgy tervezték, hogy az időintervallumokról is lehessen következtetni. Az eseménykalkulus axióma azt mondja ki, hogy egy folyó esemény igaz egy időpontban, ha a folyó eseményt valamilyen múltbeli esemény kezdeményezte, és időközben a folyó eseményt semmilyen közbenső esemény nem állította le. Az Inicializál és a Leállít relációk a szituációkalkulus-beli Eredmény relációhoz hasonló szerepet töltenek be. Az Inicializál(e, f, t) azt jelenti, hogy az e esemény t időpontban történő bekövetkezése az f folyó eseményt igazzá teszi, míg a Leállít(w, f, t) jelentése, hogy f igaz értéke megszűnt. A Történik(e, t) azt fogja jelenteni, hogy az e esemény a t időpontban történik, a Levág(f, t, t2)-t pedig arra fogjuk használni, hogy leírhassuk, hogy az f-et valamilyen esemény a t és a t2 időpontok között leállította. Formálisan az axióma a következő:
Eseménykalkulus Axióma:
T(f, t2) ⇔ ∃e, t Történik(e, t) ∧ Inicializál(e, f, t) ∧ (t < t2) ∧ ¬Levág(f, t, t2)
Levág(f, t, t2) ⇔ ∃e, t1 Történik(e, t1) ∧ Leállít(e, f, t1) ∧ (t < t1) ∧ (t1 < t2)
A kapott funkcionalitás hasonlít a szituációkalkulusra, azonban az időpontokról és az időintervallumokról is nyilatkozhatunk. Így képesek vagyunk a Történik(Kikapcs(LámpaKapcs1), 1:00)-val azt mondani, hogy a lámpakapcsolót pontosan 1:00-kor kapcsolták ki.
Az eseménykalkulus számos továbbfejlesztését dolgozták ki, hogy a közvetett hatásokkal, a nem zérus időtartalmú eseményekkel, a folyamatosan változó eseményekkel, a nemdeterminisztikus hatásokkal, a kauzális korlátozásokkal és más bonyodalmakkal is tudjanak dolgozni. Egyes kérdésekkel a következő alfejezetben fogunk találkozni. A tisztesség kedvéért megjegyezzük, hogy teljesen elfogadható megoldások máig sem születtek, azonban legyőzhetetlen akadályok sem merültek fel.
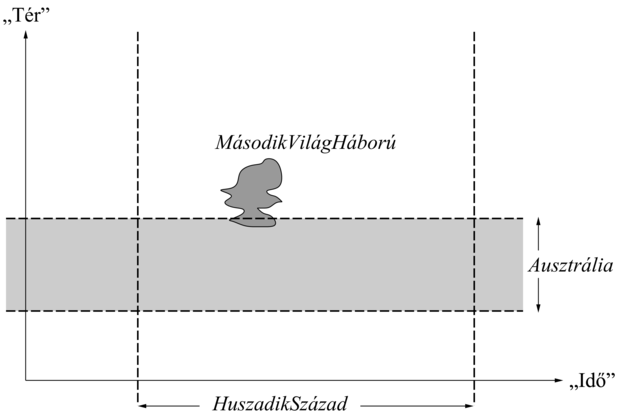
Egyelőre két fő fogalommal – a cselekvésekkel és az objektumokkal – foglalkoztunk. Ideje most utánanézni annak, hogyan illeszkednek ezek a fogalmak egy olyan befogadó ontológiába, ahol mind a cselekvések, mind az objektumok a fizikai univerzum aspektusának foghatók fel. Egy konkrét univerzumról feltesszük, hogy térbeli és időbeli dimenziója is van. A wumpus világ a kétdimenziós rács által definiált térbeli dimenzióval és diszkrét idővel rendelkezett. A világ térben háromdimenziós és időben egydimenziós,[97] mely dimenziók mindegyike folytonos. Egy általánosított esemény (generalized event) a többdimenziós univerzum egy részének – a „tér-idő darabkának” – aspektusaiból áll össze. Ez az absztrakció az eddig látott fogalmak többségét általánosítja, a cselekvéseket, a lokációkat, az időket, a folyó eseményeket és a fizikai objektumokat beleértve. Az általános ötletet a 10.3. ábra szemlélteti. Mostantól kezdve az „esemény” egyszerű fogalommal az általánosított eseményeket fogjuk nevezni.
A második világháború például egy olyan esemény, amely a tér-idő különböző pontjaiban történt meg, ezt a szabálytalan szürke folt jelzi. Az eseményt a részeseményekre (subevents)[98] bonthatjuk szét:
RészEsemény(AngliaiCsata, MásodikVilágHáború)
Hasonlóképpen a második világháború a 20. század részeseménye:
RészEsemény(MásodikVilágHáború, HuszadikSzázad)
A 20. század az időnek egy intervalluma. Intervallumok a tér-idő olyan darabkái, amelyek két időpont között az egész teret tartalmazzák. A Periodus(e) függvény az e eseményt bezáró legkisebb intervallumot jelöli. A Tartam(i) egy intervallum által foglalt idő hossza, mondhatjuk tehát, hogy Tartam(Periodus(MásodikVilágHáború)) > Év(5).
Ausztrália egy hely, egy darabka rögzített térbeli határokkal. A határok időben változnak, geológiai vagy politikai okoknál fogva. A Benne predikátumot fogjuk használni az olyan részesemény reláció megjelölésére, amely akkor áll fenn, ha egy esemény térbeli vetülete Része egy másik esemény vetületének:
Benne(Sydney, Ausztrália)
A Hely(e) függvény az e eseményt befogadó legkisebb helyet jelenti.
Mint minden más objektumot, az eseményeket szintén lehet kategóriákba szervezni. A MásodikVilágHáború például a Háború kategóriába tartozik. Azt, hogy Angliában 1640-ben polgárháború zajlott, a következőképpen mondhatjuk:
∃w w ∈ PolgárHáború ∧ RészEsemény(w, 1640) ∧ Benne(Lokáció(w), Anglia)
Az eseménykategória fogalma segít megválaszolni azt a kérdést, amit igyekeztünk elkerülni, amikor a 10.3. alfejezetben a cselekvések hatásairól beszéltünk. Mire hivatkoznak pontosan az olyan logikai termek, mint a Megy([1, 1], [1, 2])? Események ezek?
A válasz, talán meglepő, de az, hogy nem. Ennek megértéséhez nézzünk meg két „azonos” cselekvést tartalmazó tervet, mint például:
[Megy([1, 1], [1, 2]), Megy([1, 2], [1, 1]), Megy([1, 1], [1, 2])]
Ebben a tervben a Megy([1, 1], [1, 2]) nem lehet egy esemény neve, mert két különböző esemény van, amelyek különböző időpontban történnek meg. Helyette a Megy([1, 1], [1, 2]) egy eseménykategória neve – azoké az eseményeké, amikor az ágens az [1, 1]-ről az [1, 2]-re lép át. A háromlépéses terv azt mondja ki, hogy e három eseménykategória példányai fognak előfordulni.
Jegyezzük meg, hogy ez az első alkalom, amikor a kategóriák megnevezésére komplex termeket vetettünk be, egyszerű konstansszimbólumok helyett. Ez nem jelent új nehézséget. Az argumentumstruktúrát valójában a hasznunkra is fordíthatjuk. Az argumentumok eliminálása az általánosabb kategóriák bevezetését teszi lehetővé:
Megy(x, y) ⊆ MegyHová(y) Megy(x, y) ⊆ MegyHonnan(x)
Hasonlóan, argumentumok hozzáadásával még specifikusabb kategóriákat hozhatunk létre. Más ágensek cselekvéseinek leírásához például hozzáadhatjuk az ágenseket jelölő argumentumot. Így ahhoz, hogy azt mondhassuk, hogy „tegnap Shankar New Yorkból Újdelhibe utazott”, azt írhatnánk, hogy:
∃e e ∈ Repül(Shankar, NewYork, Újdelhi) ∧ RészEsemény(e, Tegnap)
Az állítás e formája annyira gyakori, hogy külön rövidítést fogunk rá alkalmazni: E(c, i), aminek az a jelentése, hogy a c eseménykategória egy eleme egy i intervallum, vagy az esemény részeseménye:
E(c, i) ⇔ ∃e e ∈ c ∧ RészEseménye(e, i)
Így:
E(Repül(Shankar, NewYork, Újdelhi), Tegnap)
Az eddig látott események meghatározott struktúrával rendelkező diszkrét események (discrete events) voltak. Shankar utazásának van kezdete, közepe és vége. Ha félbeszakítjuk, az esemény megváltozik – nem lesz többé egy New York és Újdelhi közötti utazás, hanem helyette egy New York és egy Európában valahol fekvő pont közötti utazás. A Repül(Shankar) által jelölt eseménykategóriának ezzel szemben más a jellege. Ha Shankar repülésének egy rövid intervallumát vesszük, mondjuk a harmadik 20 perces időszakaszát (amikor is türelmetlenül várja már a második csomag mézben pörkölt földimogyorót), ez az esemény még mindig a Repül(Shankar) egy része. Valójában ez akármilyen részintervallum esetében is igaz.
Az ilyen tulajdonságú események kategóriáit folyamat- (process) kategóriáknak, illetve folytonos esemény (liquid event) kategóriáknak nevezzük. Egy folyamat akármilyen részintervalluma ugyanannak a folyamatkategóriának a tagja. A diszkrét eseményekre kialakított jelölést alkalmazva mondhatjuk például, hogy Shankar valamikor tegnap repült:
E(Repül(Shankar), Tegnap)
Gyakran ki szeretnénk jelenteni, hogy valamilyen folyamat egy teljes intervallumon keresztül tartott, és nem csak annak valamilyen részintervallumában. Erre T predikátumot fogjuk használni:
T(Dolgozik(István), MaiEbédIdő)
T(c, i)-nek az a jelentése, hogy egy c típusú esemény az egész i intervallum ideje alatt tartott – azaz az esemény pontosan akkor kezdődik és fejeződik be, amikor az intervallum.
Folyékony és nem folyékony események közötti megkülönböztetés pontosan analóg a szubsztanciák, avagy az anyag és az egyedi objektumok közötti különbséggel. Tény, hogy egyes kutatók folyékony eseményeket temporális szubsztanciáknak (temporal substances) nevezték el, míg a vajszerű dolgok térbeli szubsztanciák (spatial substances).
A folytonos események a folyamatosan változó folyamatokon túlmenően képesek a folyamatosan nem változó folyamatok leírására is. Ezeket gyakran állapotoknak (states) nevezzük. A „Shankar New Yorkban tartózkodik” például egy olyan állapotkategória, amit Benne(Shankar, NewYork)-kal lehetne jelölni. Azt, hogy Sankar az egész mai napot New Yorkban töltötte, úgy írhatnánk, hogy:
T(Benne(Shankar, NewYork), Ma)
Primitív állapotok vagy események kombinálásával bonyolultabb képződményeket is kialakíthatunk. Ez a megközelítés a folyó esemény kalkulus (fluent calculus). A folyó esemény kalkulus nem egyedi folyó eseményeket, hanem folyó események kombinációit reifikálja. Láttuk már annak a módját, hogy az egyszerre történő két dolog eseményét hogyan reprezentáljuk, azaz láttuk a Mindkettő(e1, e2) függvényt. A folyó kalkulusban ezt általában az e1 o e2 infix jelöléssel rövidítik. Hogy megmondhassuk, hogy például „valaki sétált és közben rágógumit rágott”, azt írhatjuk, hogy:
∃p, i (p ∈ Ember) ∧ T(Sétál(p) o RágótRág(p), i)
A „o” függvény kommutatív és asszociatív, pontosan úgy, mint a logikai konjunkció. Definiálhatjuk a diszjunkció és a negálás analógiáját is, azzal viszont óvatosabban kell eljárnunk, mivel a diszjunkciót kétféle módon lehet értelmesen interpretálni. Amikor azt mondjuk, hogy „az ágens az utóbbi két percben vagy sétált, vagy rágógumit rágott”, gondolhatunk arra, hogy az ágens az egész idő alatt az egyik cselekvést végezte, vagy pedig, hogy a két cselekvést felváltva tette. E két lehetőség megjelölésére az Egyik és a VagyVagy függvényeket fogjuk használni. A komplex eseményeket a 10.4. ábra szemlélteti.
Az idő fontos minden cselekvő ágens számára, és az időintervallumok reprezentálására számos erőfeszítés történt. Az időintervallumok két fajtájával foglalkozunk: az időpillanatokkal és a kiterjesztett intervallumokkal. A különbség köztük az, hogy csak az időpillanatnak lehet zérus időtartama:
Partíció({IdőPillanatok, KiterjesztettIntervallumok}, IdőIntervallumok)
i ∈ IdőIntervallumok ⇔ (Tartam(i) = Másodperc(0)
Most egy időskálát konstruálunk, amelynek pontjait időpillanatokhoz rendeljük hozzá; ezzel abszolút időpontokat kapunk. Az időskála tetszőleges lehet. Az időt másodpercekben fogjuk mérni, és kimondjuk, hogy a 0. idő az 1900. január 1-jei (GMT) éjfél. A Kezdet és a Vég függvények az időintervallum legkorábbi és a legkésőbbi időpillanatát adják vissza, az Idő függvény egy időpillanathoz tartozó pontot keres ki az időskálán. Az IdőTartam függvény megadja a kezdeti idő és a végidő közötti különbséget.
IdőIntervallum(i) → IdőTartam(i) = (Idő(Vége(i)) – Idő(Kezdete(i)))
Idő(Kezdete(AD1900)) = Másodperc(0)
Idő(Kezdete(AD2001) = Másodperc(3187324800)
Idő(Vége(AD2001)) = Másodperc(3218860800)
IdőTartam(AD2001) = Másodperc(31536000)
Hogy a számokat könnyebb legyen olvasni, vezessünk be egy határgumentumú Dátum függvényt (óra, percek, másodpercek, hónap, nap és év), melynek visszaadott értéke egy pont az időskálán:
Idő(Kezdete(AD2001)) = Dátum(0, 0, 0, 1, Január, 2001)
Dátum(0, 20, 21, 24, 1, 1995) = Másodperc(3000000000)
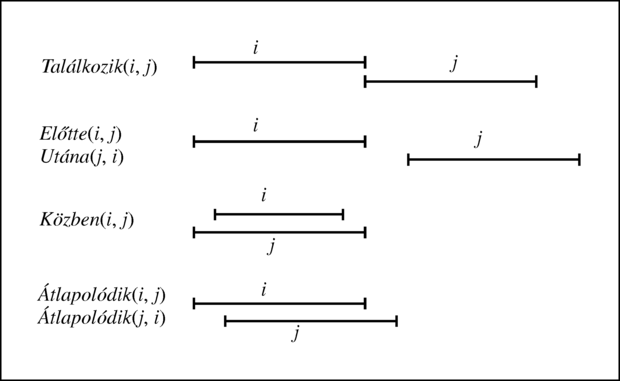
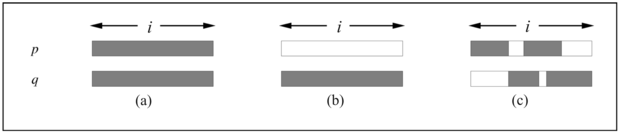
Két intervallum Találkozik, ha az egyiknek a végideje megegyezik a másiknak a kezdeti idejével. Már egyedül a Találkozik segítségével is lehetséges olyan további predikátumokat definiálni, mint az Előtte, az Utána, a Közben és az Átlapolódik. Azonban sokkal intuitívebb, ha a definiálásuk az időskála pontjainak segítségével történik (lásd 10.5. ábrán a grafikus reprezentációt).
Találkozik(i, j) ⇔ Idő(Vége(i)) = Idő(Kezdete(j))
Előtte(i, j) ⇔ Idő(Vége(i)) < Idő(Kezdete(j))
Utána(j, i) ⇔ Előtte(i, j)
Közben(i, j) ⇔ Idő(Kezdete(j)) ≤ Idő(Kezdete(i)) ∧ Idő(Vége(i)) ≤ Idő(Vége(j))
Átlapolódik(i, j) ⇔ ∃k Közben(k, i) ∧ Közben(k, j)
Annak megadására, hogy II. Erzsébet uralkodása VI. György uralkodását követte, Elvis uralkodása viszont az 1950-es évekkel átlapolódott, a következőt írhatjuk:
Utána(Uralkodása(II.Erzsébet), Uralkodása(VI.György))
Átlapolódik(ÖtvenesÉvek, Uralkodása(Elvis))
Kezdete(ÖtvenesÉvek) = Kezdete(AD1950)
Vége(ÖtvenesÉvek) = Vége(AD1950)
Említettük, hogy fizikai objektumokat általánosított objektumoknak lehet tekinteni, abban az értelemben, hogy egy objektum a tér-idő egy darabkája. Az USA például egy olyan eseménynek képzelhető el, amely mondjuk 1776-ban, 13 állam uniójaként kezdődött és ma, 50 állam uniójaként, még folyamatban van. Az USA változó aspektusait állapot folyó eseményekkel írhatjuk le. Mondhatjuk például, hogy valamikor, az 1999. évben a lakossága 271 millió fő volt:
E(Lakosság(USA, (271000000), AD1999)
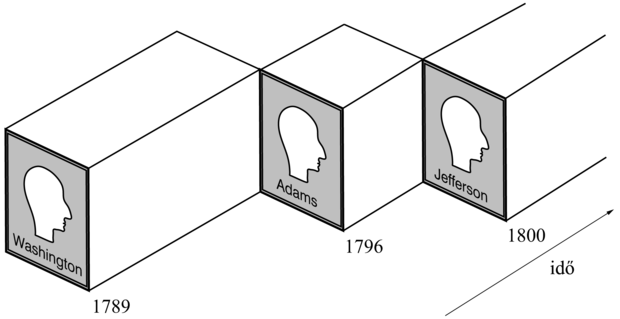
Egy másik ilyen aspektus, amely a szerencsétlenségektől eltekintve, négy- vagy nyolcévenként változik, az ország elnöke. Felvehető, hogy az Elnök(USA) egy olyan logikai term, amely különböző időkben különböző objektumokat jelent. Ez sajnos nem lehetséges, mert egy term egy adott modellstruktúrában pontosan egy objektumot jelöl meg. (Az Elnök(USA, t) jelölhetne különböző objektumokat t értékének megfelelően, az ontológiánk azonban az időpontokat és a folyó eseményeket szétválasztja.) Egyetlen lehetőség, hogy az Elnök(USA) egy olyan egyedi objektumot jelöl, amely különböző időkben különböző emberekből áll. Az Elnök(USA), mint objektum, George Washington volt 1789-tól 1796-ig, John Adams volt 1796-tól 1800-ig stb. (lásd 10.6. ábra). Azt, hogy George Washington 1790-ben elnök volt, a következőképpen írhatjuk le:
T(Elnök(USA) = GeorgeWashington, AD1790)
Azonban óvatosnak kell lenni. Ebben a mondatban az „=” inkább egy függvény, és nem egy standard logikai operátor. Az interpretáció nem az, hogy GeorgeWashington és az Elnök(USA) 1790-ben logikailag azonosak. A logikai azonosság nem olyan dolog, ami időben változhat. A logikai azonosság az egyes objektumok azon részeseményei között áll fenn, amelyeket az 1790-es elnöki periódus definiált.
Ne tévessze össze a GeorgeWashington fizikai objektumot az atomok egy gyűjteményével. George Washington logikailag nem azonos semmilyen konkrét atomgyűjteménnyel, mert az az atomhalmaz, amiből áll, időben lényegesen változik. Neki rövid élettartama van, minden atomnak saját hosszú élettartama van. Bizonyos periódusban metszik egymást, amikor is az atom temporális szelete a RészEseménye George-nak, majd külön útjukat járják.
[96] Ez lényegében az a megközelítés, amit a 7. fejezetben a logikai áramkör-ágens tervezésénél alkalmaztunk. Az olyan axiómákat, mint a (7.4) és a (7.5), valóban követő állapot axiómáknak lehet nézni.
[97] A füzérelméletet tanulmányozó néhány fizikus a 10 vagy több dimenzió mellett foglal állás, mások diszkrét világról beszélnek, a 4-D folytonos tér-idő azonban a józan ész következtetési céloknak megfelelő reprezentáció.
[98] Jegyezzük meg, hogy a RészEsemény a Része reláció speciális esete, és ugyanúgy tranzitív és reflexív.