6.3. Alfa-béta nyesés
A minimax keresés problémája, hogy a játékban a megvizsgálandó állapotok száma exponenciális a lépések számában. A kitevőtől sajnos megszabadulni nem tudunk, ám lényegében megfelezhetjük. A trükk az, hogy lehetséges a korrekt minimax döntés kiszámítása anélkül, hogy a játékfában minden csomópontra rá kelljen nézni. Ehhez kölcsönözhetjük a 4. fejezetben megismert nyesés (prunning) gondolatát, és a játékfa nagyobb részét a megfontolásokból kihagyhatjuk. A konkrét vizsgált technika az alfa-béta nyesés (alpha-beta prunning). Ha ezt egy standard minimax fára alkalmazzuk, ugyanazt az eredményt adja vissza, mint a minimax, a döntésre hatással nem lévő ágakat azonban lenyesi.
Tekintsük ismét a 6.2. ábrán látható egylépésváltásos játékfát. Kövessük még egyszer az optimális döntés kiszámításának menetét, most azonban kísérjük figyelemmel, hogy mit is tudunk valójában a folyamat minden pontjában. A lépésekhez a 6.5. ábra ad magyarázatot. Az eredmény az, hogy meg tudjuk határozni a minimax döntést anélkül, hogy a két levélcsomópontot bármikor is megnéznénk.
A módszert értelmezhetjük másképpen is, mint a MINIMAX-ÉRTÉK függvény egy egyszerűsítését. Legyen a C csomópontot a 6.5. ábrán látható, ki nem értékelt követő csomópontok értéke x és y, és legyen z a kettő minimuma. A gyökércsomópont értéke ekkor:
MINIMAX-ÉRTÉK (gyökér) = max(min(3, 12, 8), min(2, x, y), min(14, 5, 2)
= max(3, min(2, x, y), 2)
= max(3, z, 2) ahol z ≤ 2
= 3
Más szóval a gyökér értéke és így a minimax döntés független a lenyesett levelek x és y értékeitől.
Fontos
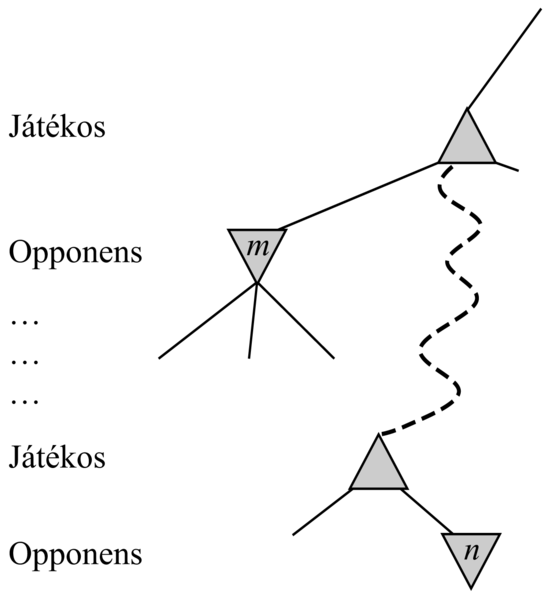
Az alfa-béta nyesést tetszőleges mélységű fákra lehet alkalmazni, és sokszor lehetséges, hogy levelek helyett teljes részfákat nyessünk le. Az általános elv az alábbi: tekintsünk egy olyan n csomópontot valahol a fa belsejében (lásd 6.6. ábra), hogy a Játékosnak lehetősége legyen e csomópontba lépni. Ha a Játékosnak van az n szülőcsomópontjánál vagy ettől feljebb bármelyik döntési pontban egy jobb választása, m, akkor az n-t az aktuális játékban soha nem érjük el. Ha az n-ről tehát (néhány követőjének megvizsgálásával) már eleget tudunk, hogy ehhez a konklúzióhoz jussunk, a csomópontot nyugodtan lenyeshetjük.
Emlékezzünk, hogy a minimax keresés mélységi keresés, egy adott időben tehát elegendő a fában egy egyedi út menti csomópontokkal foglalkozni. Az alfa-béta nyesés megnevezése két paramétertől származik, mely paraméterek az út mentén megjelenő visszaléptetett értékek korlátjaira vonatkoznak:
α = az út mentén tetszőleges döntési pontban a MAX számára eddig megtalált legjobb (azaz a legmagasabb értékű) választás értéke.
β = az út mentén tetszőleges döntési pontban a MIN számára eddig megtalált legjobb (azaz a legkisebb értékű) választás értéke.
MIN csomópont, legfeljebb 3 értékű. (b) A B alatti második csomópontnak 12 az értéke. MIN ezt a lépést elkerüli, így B értéke még mindig legfeljebb 3. (c) A B alatti harmadik levélnek 8 az értéke. B összes követőit láttuk már, B értéke tehát pontosan 3. Most azt következtethetjük ki, hogy a gyökér értéke legalább 3, mert MAX-nak a gyökérben 3-as értékű választása van. (d) A C alatti első levélnek 2 az értéke. C tehát, ami egy MIN csomópont, legfeljebb 2 értékű. De mi tudjuk már, hogy B-nek 3 az értéke, MAX tehát C-t soha nem fogja választani. Azért nem is érdemes C további követőit megvizsgálni. Ez az alfa-béta nyesés egy példája. (e) A D alatti első levélnek 14 az értéke, így D értéke legfeljebb 14. Ez több mint MAX legjobb alternatívája (azaz 3), meg kell vizsgálni ezért D követőit. Jegyezzük meg, hogy most a gyökér minden követője esetén rendelkezünk értékkorláttal, a gyökér értéke legfeljebb 14. (f) D második követőjének értéke 5, így tovább kell folytatnunk a vizsgálatot. A harmadik követő értéke 2, D értéke tehát pontosan 2. MAX döntése a gyökérnél, hogy B felé kell lépni, 3-as értékkel.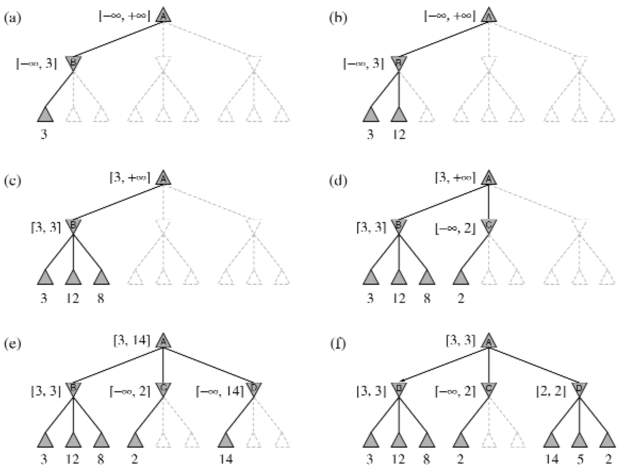
Az alfa-béta keresés az α és a β értékeit munka közben frissíti, és a csomópontnál a megmaradó ágakat lenyesi (a rekurzív hívást terminálja), amint csak biztossá válik, hogy az aktuális csomópont értéke rosszabb lesz, mint az aktuális α és β érték, MAX-ra, illetve MIN-re. A teljes algoritmust a 6.7. ábra mutatja. Bátorítjuk az olvasót, hogy a 6.5. ábrán látható fára alkalmazva, kövesse végig az algoritmus működését.
Az alfa-béta nyesés hatékonysága erősen függ a követő csomópontok vizsgálatának sorrendjétől. Például a 6.5. (e) és (f) ábrán D egyetlen követőjét sem lehetne lenyesni, mert először a legrosszabb követőt (MIN szemszögéből) generáltuk. Ha a harmadik követőt elsőnek generálnánk, a maradó kettőt le lehetne nyesni. Ez azt sugallja, hogy érdemes lenne először a legjobbnak tűnő csomópontokat megvizsgálni.
Ha feltételezzük, hogy ez megtehető,[56] akkor az alfa-béta nyesésnek elég az O(bm/2) csomópontot megvizsgálni, a legjobb lépés kiszámításához, a minimax O(bm) értékével szemben. Ez azt jelenti, hogy az effektív elágazási tényező b helyett 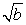 lesz – például a sakk esetében 35 helyett 6. Más szóval, az alfa-béta nyesés ugyanannyi idő alatt kétszer olyan messzire néz, mint a minimax. Ha a követő csomópontokat véletlen sorrendben vizsgálnánk a legjobbat-először helyett, a vizsgált csomópontok össz-száma O(b3m/4) lenne, mérsékelt értékű b-kre. A sakk esetében egy igen egyszerű rendezőfüggvény (mint például az, hogy először a leütésekkel, majd a támadásokkal, ezt követően az előrelépésekkel és végül a hátralépésekkel próbálkozunk) a legjobb esetre vonatkozó O(bm/2) eredményt egy 2-es tényező erejéig közelíti meg. Dinamika hozzáadása a lépésrendező sémákhoz, mint például azokkal a lépésekkel próbálkozni először, amelyek legutóbb a legjobbnak bizonyultak, az elvi korláthoz egészen közel visz.
lesz – például a sakk esetében 35 helyett 6. Más szóval, az alfa-béta nyesés ugyanannyi idő alatt kétszer olyan messzire néz, mint a minimax. Ha a követő csomópontokat véletlen sorrendben vizsgálnánk a legjobbat-először helyett, a vizsgált csomópontok össz-száma O(b3m/4) lenne, mérsékelt értékű b-kre. A sakk esetében egy igen egyszerű rendezőfüggvény (mint például az, hogy először a leütésekkel, majd a támadásokkal, ezt követően az előrelépésekkel és végül a hátralépésekkel próbálkozunk) a legjobb esetre vonatkozó O(bm/2) eredményt egy 2-es tényező erejéig közelíti meg. Dinamika hozzáadása a lépésrendező sémákhoz, mint például azokkal a lépésekkel próbálkozni először, amelyek legutóbb a legjobbnak bizonyultak, az elvi korláthoz egészen közel visz.
A 3. fejezetben megjegyeztük, hogy a keresési fában az ismétlődő állapotok a keresési költségekben exponenciális növekedéshez is vezethetnek. Játékokban gyakran előfordulnak ismétlődő állapotok a transzpozíciók (transpositions) – a lépési szekvenciának az ugyanahhoz az álláshoz vezető különböző permutációi – miatt. Ha például Fehér lépése a1, amire Fekete b1 lépéssel válaszolhat, és a tábla más részén van egy vele nem kapcsolatos a2 lépése, amire Fekete b2-vel válaszolhat, akkor az [a1, b1, a2, b2] és az [a1, b2, a2, b1] szekvenciák mind ugyanabban az állásban végződnek (ahogy ebben az állásban végződik az előbbi lépések minden a2-vel kezdődő permutációja). Érdemes ennek az állásnak a kiértékelését az első előforduláskor egy hash-táblában eltárolni, mert így a későbbi előfordulásoknál a kiszámítás megismétlését megspóroljuk.
Az előbb látott pozíciók hash-tábláját hagyományosan transzpozíciós táblának (transposition table) hívják. Ez lényegében azonos a GRÁF-KERESÉS zárt listájával 3.5. szakasz - Az Ismételt állapotok elkerülése. A transzpozíciós tábla használata drámai hatású lehet és a sakkban néha az elérhető mélység megduplázásához vezet. Másrészt ha másodpercenként a csomópontok millióit értékeljük ki, nem praktikus ezeket mind a transzpozíciós táblában tartani. A legértékesebb csomópontok megválasztására különböző stratégiákat dolgoztak ki.
MAX-ÉRTÉK és a MIN-ÉRTÉK hívásokban, ahol az α és a β értékeket kezeli (és adminisztrálja e paraméterek átadását).
[56] Természetesen nem tökéletes módon, különben a sorbarendező-függvény segítségével egy hibátlan játékot tudnánk játszani.

