5.2. A visszalépéses keresés alkalmazása kényszerkielégítési problémákra
Az előző alfejezetben keresési problémaként fogalmaztuk meg a kényszerkielégítési problémákat. Ezt a megfogalmazást felhasználva a 3. és a 4. fejezetben bemutatott bármely keresési eljárással megoldhatók a kényszerkielégítési problémák. Tegyük fel, hogy alkalmazzuk a szélességi keresést az előző fejezetben megadott általános CSP-megfogalmazásra. Hamarosan valami szörnyűség tűnik fel: a fa tetején az elágazási tényező nd, mert a d érték bármelyike hozzárendelhető az n változó bármelyikéhez. A következő szinten az elágazási tényező (n – 1)d és így tovább az n szint során. Egy n!· dn levelű fát építünk fel, noha csupán dn lehetséges teljes hozzárendelés van!
Fontos
Látszólag racionális, valójában naiv problémamegfogalmazásunk elhanyagolta az összes kényszerkielégítési probléma egy döntő közös tulajdonságát: a kommutativitást (commutativity). Egy probléma akkor kommutatív, ha a végeredmény szempontjából közömbös, hogy cselekvések egy adott sorozatát milyen sorrendben alkalmazzuk. Ilyenek a kényszerkielégítési problémák is, mert a változók hozzárendelése során a sorrendtől függetlenül ugyanazt a parciális hozzárendelést kapjuk. Ezért tehát mindegyik kényszerkielégítési problémamegoldó a következő állapot generálásakor a keresési fa minden csomópontjában csak egyetlen változó lehetséges hozzárendeléseit veszi tekintetbe. Az ausztráliai térképszínezési probléma keresési fájának gyökércsomópontjában választhatunk a DA = vörös, a DA = zöld és a DA = kék közül, de sohasem merül fel választási lehetőségként a DA = vörös vagy az NyA = kék. A levelek száma ezzel a megszorítással már a remélt dn.
HOZZÁRENDELETLEN-VÁLTOZÓ-KIVÁLASZTÁSA és a TARTOMÁNY-ÉRTÉKEK-SORRENDEZÉSE függvények használhatók a szövegben bemutatott általános célú heurisztikák megvalósítására.
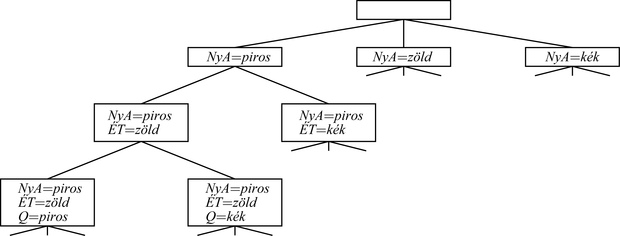
A visszalépéses keresés (backtracking search) kifejezést olyan mélységi keresésekre használjuk, melyek egyszerre csak egy változóhoz rendelnek értéket, és visszalépnek, ha már nincs megengedett hozzárendelési lehetőség. Az algoritmus az 5.3. ábrán látható. Vegyük észre, hogy az algoritmus lényegében a 115–116. oldalon leírt egyenkénti módszert használja az inkrementális következő állapot generálásra. Továbbá a következő állapot generálásakor kifejti az aktuális állapotot, nem pedig egyszerűen másolja. A kényszerkielégítési problémák szokásos reprezentációja miatt nincs szükség a VISSZALÉPÉSES-KERESÉS algoritmus kiegészítésére tárgyterület-specifikus kezdeti állapottal, állapotátmenet-függvénnyel vagy célteszttel. Az 5.4. ábrán látható egy részlet az ausztráliai színezési problémához generált keresési fából (a változó-hozzárendelések sorrendje NyA, ÉT, Q, …).
Az egyszerű visszalépéses keresés a 3. fejezet terminológiája szerint nem informált algoritmus, tehát nem is várjuk el, hogy nagy problémák esetén is hatékony legyen. Az 5.5. ábra első oszlopában bemutatott néhány eredmény megerősíti várakozásainkat.

A 4. fejezetben a nem informált keresési algoritmusok gyenge teljesítményét a probléma ismeretéből származó tárgyterület-specifikus heurisztika bevezetésével orvosoltuk. Az derül azonban ki, hogy a kényszerkielégítési problémák hatékonyan megoldhatók ilyen tárgyterület-specifikus tudás nélkül is. Olyan általános célú eljárások alakíthatók ki, amelyek az alábbi kérdéseket vizsgálják:
-
A következő lépésben melyik változóhoz rendeljünk értéket, és milyen sorrendben próbálkozzunk az értékekkel?
-
Milyen következményei vannak a jelenlegi változó-hozzárendeléseknek a még hozzárendeletlen változók számára?
-
Ha egy út sikertelennek bizonyul (azaz egy olyan állapothoz jutunk, ahol egy változónak nincs megengedhető értéke), a következő utak során el tudja-e kerülni a keresés ezt a hibát?
A következő pontokban megpróbáljuk sorra megválaszolni ezeket a kérdéseket.
A visszalépéses algoritmus tartalmazza az alábbi sort:
var ← Hozzárendeletlen-Változó-Kiválasztás(Változók[csp], hozzárendelések, csp)
Alapértelmezés szerint a HOZZÁRENDELETLEN-VÁLTOZÓ-KIVÁLASZTÁS egyszerűen kiválasztja a VÁLTOZÓK[csp] lista sorrendje szerinti következő hozzárendeletlen változót. A statikus változó-hozzárendelés ritkán vezet a leghatékonyabb kereséshez. Például miután kiválasztottuk az NyA = vörös és az ÉT = zöld hozzárendeléseket, csak egyetlen értéket rendelhetünk DA-hoz, tehát ésszerű lenne inkább a DA = kék hozzárendelést elvégezni, mintsem Q számára keresni értéket. Sőt miután DA értéket kapott, kényszerítve vagyunk Q, ÚDW és V értékeinek kiválasztásakor. Ezt az intuitív ötletet (a legkevesebb „megengedett” értékkel rendelkező változó kiválasztását) nevezik legkevesebb fennmaradó érték (minimum remaining values, MRV) heurisztikának. Nevezték már „legkorlátozottabb változó” vagy „meghiúsulást előre” heurisztikának is (az utóbbi névnek az a magyarázata, hogy azt a változót emeli ki, amelyik legvalószínűbben fog hamarosan hibához vezetni, ezáltal megnyesve a keresési fát). Ha van egy X változó, amelynek egyetlen megengedett értéke sincs, akkor az MRV-heurisztika ki fogja választani X-et, és azonnal kideríti a hibát, elkerülve ezzel a többi változó közötti értelmetlen keresgélést, ami mindig kudarcra vezet, amikor X végül is kiválasztódik. Az 5.5. ábra második, BT+MRV címkéjű oszlopa ennek a heurisztikának a teljesítményét mutatja. Az egyszerű visszalépéses keresésnél a teljesítmény a problémától függően mintegy 3…3000-szer jobb lehet. Vegyük észre, hogy a teljesítménymértékünk nem tartalmazza a heurisztikus értékek kiszámításának többletköltségét. A következő pontban bemutatunk egy módszert, amellyel kezelhetővé válik ez a költség.
Az MRV-heurisztika semmit sem segít abban, hogy melyik régiót válasszuk ki elsőként Ausztrália kiszínezésekor, mert a kiinduláskor mindegyik régiónak három megengedett színe van. Ebben az esetben segíthet a fokszám-heurisztika (degree heuristics). Ez azáltal kísérli meg a későbbi választások elágazási tényezőjét csökkenteni, hogy azt a változót választja ki, amely a legtöbbször szerepel a hozzárendeletlen változókra vonatkozó kényszerekben. Az 5.1. ábrán DA a legnagyobb fokszámú változó (fokszáma 5), az összes többi változó fokszáma 2 vagy 3, leszámítva T-t, amelyé nulla. Valójában, ha már egyszer DA-t kiválasztottuk, a fokszám-heurisztika alkalmazása a problémát egyetlen hibás lépés nélkül oldja meg: mindegyik választási pontnál bármelyik konzisztens színt is választjuk, mindenképpen visszalépés nélkül jutunk egy megoldáshoz. A legkevesebb fennmaradó érték heurisztika általában jobban irányít, de a patthelyzetek eldöntéséhez hasznos segítség lehet a fokszám-heurisztika.
Miután az algoritmus már kiválasztott egy változót, el kell döntenie, hogy milyen sorrendben vizsgálja meg ennek értékeit. Erre néha a legkevésbé-korlátozó-érték (least-constraining-value) heurisztika lehet hasznos. Ez a heurisztika előnyben részesíti azt az értéket, amely a legkevesebb választást zárja ki a kényszergráfban a szomszédos változóknál. Például tegyük fel, hogy az 5.1. ábra esetében már létrehoztuk az NyA = vörös és az ÉT = zöld parciális hozzárendelést, és most Q számára akarunk értéket találni. A kék rossz választás volna, mert ez kizárja Q szomszédjának, DA-nak utolsó megengedett értékét. A legkevésbé korlátozó heurisztika ezért a kékkel szemben a vöröset részesíti előnyben. Általában véve a heurisztika megpróbálja a későbbi változó-hozzárendelések számára a lehető legnagyobb szabadságot meghagyni. Természetesen ha egy probléma összes megoldását meg szeretnénk találni, és nem elégszünk meg csupán eggyel, akkor a sorrend közömbös, hiszen úgyis minden értéknek sorra kell kerülnie. Ugyanez igaz akkor is, ha a problémának nincsen megoldása.
A keresési algoritmusunk eddig csak akkor foglalkozott egy változóra vonatkozó kényszerrel, ha a változót a HOZZÁRENDELETLEN-VÁLTOZÓ-KIVÁLASZTÁS kiválasztotta. De ha néhány kényszert a keresés folyamán korábban vagy akár még a keresés megkezdése előtt megvizsgálunk, akkor drasztikusan csökkenthető a keresési tér mérete.
A kényszerek keresés közbeni jobb felhasználásának egyik módszerét előrenéző ellenőrzésnek (forward checking) nevezzük. Az előrenéző ellenőrzési folyamat minden egyes alkalommal, amikor egy X változó értéket kap, minden, az X-hez kényszerrel kötött, hozzárendeletlen Y-t megvizsgál, és Y tartományából törli az X számára választott értékkel inkonzisztens értékeket. Az 5.6. ábra bemutatja az előrenéző ellenőrzéses keresés menetét a térképszínezési probléma során. Két fontos dolgot kell megemlítenünk ezzel a példával kapcsolatban. Először is vegyük észre, hogy miután elvégeztük az NyA = vörös és a Q = zöld hozzárendeléseket, ÉT és DA tartományai egyetlen elemre szűkültek, és azzal, hogy az NyA-ból és a Q-ból származó információt terjesztettük, teljesen megszüntettük az ezen változók szerinti elágazást. Az MRV-heurisztika, amely az előrenéző ellenőrzés nyilvánvaló partnere, automatikusan DA-t és ÉT-t választja következőnek. (Tulajdonképpen még hatékonyabb eljárássá tehetjük az előrenéző ellenőrzést, ha az MRV-heurisztika munkájához szükséges információt inkrementálisan számítjuk.) A másik dolog, amire érdemes felfigyelni, az az, hogy a V = kék hozzárendelés után DA tartománya üres lett. Ezért az előrenéző ellenőrzés megállapítja, hogy a {NyA = vörös, Q =zöld, V = kék} részleges hozzárendelés inkonzisztens a probléma kényszereivel, és az algoritmus azonnal visszalép.
Az előrenéző ellenőrzés ugyan sok inkonzisztenciát észrevesz, de nem mindet. Például nézzük csak az 5.6. ábra harmadik sorát. Az látható itt, hogy amikor DA vörös és Q zöld, mind ÉT-nek, mind DA-nak kéknek kell lennie. De ezek szomszédosak, és nem lehet azonos az értékük. Az előrenéző ellenőrzés nem veszi észre ezt az inkonzisztenciát, mert nem néz elég messze előre. A kényszerek terjesztése (constraint propagation) általános kifejezés jelöli azt, ha az egyik változó kényszerének a többi változót érintő következményeit terjesztjük: esetünkben NyA-ról Q-ra és ÉT-ről DA-ra kell terjeszteni (ahogy ezt már az előrenéző ellenőrzés is megtette), majd az ÉT és DA közti kényszerre, hogy észrevehessük az inkonzisztenciát. Ezt pedig gyorsan szeretnénk tenni: semmi értelme a keresés méretét csökkenteni, ha több időt töltünk a kényszerek terjesztésével, mint az egyszerű kereséssel tennénk.
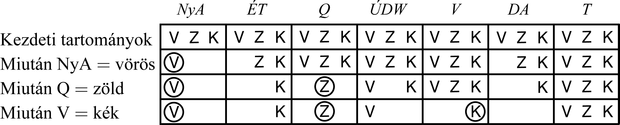
Az élkonzisztencia (arc consistency) alapul szolgálhat egy gyors, az előrenéző ellenőrzésnél lényegesen erősebb kényszerterjesztéshez. Az „él” itt a kényszergráf irányított éleit jelenti, amilyen például a DA-ból az ÚDW-be mutató él. Ha adott DA és ÚDW aktuális tartománya, akkor ez az él konzisztens, ha DA mindegyik x értékéhez található egy x-szel konzisztens valamilyen y érték ÚDW-ben. Az 5.6. ábra harmadik sorában DA és ÚDW pillanatnyi tartománya rendre a {kék}, illetve a {vörös, kék}. A DA = kék esetén található egy konzisztens hozzárendelés ÚDW-hez, nevezetesen az ÚDW = vörös; ezért a DA-ből ÚDW-be mutató él konzisztens. Viszont az ÚDW-ből a DA-ba mutató él nem konzisztens, mert az ÚDW = {kék} hozzárendelésnél a DA-hoz nem tudunk színt találni. Az él úgy tehető konzisztenssé, hogy az ÚDW tartományából töröljük a kék értéket.
A DA-ból ÚT-be mutató él mentén is alkalmazhatjuk a keresési folyamat ugyanazon fázisában az élkonzisztenciát. Az 5.6. ábra harmadik sora szerint mindkét változó értéktartománya {kék}. Ez azt eredményezi, hogy törölnünk kell a kék-et DA tartományából, amely ezzel kiürül. Az élkonzisztencia ellenőrzés tehát lehetővé teszi, hogy korábban észrevegyük az egyszerű előrenéző ellenőrzés által fel nem fedett inkonzisztenciát.
Az élkonzisztencia-ellenőrzés alkalmazható előfeldolgozó lépésként a keresés megkezdése előtt, vagy a keresési folyamat minden egyes hozzárendelését követő terjesztési lépésként (az előrenéző ellenőrzéshez hasonlóan). (Az utóbbi algoritmust Élkonzisztencia fenntartásának is, angol rövidítéssel MAC-nak nevezik.) Mindkét esetben addig kell ismételve alkalmazni a folyamatot, amíg nem marad inkonzisztencia. Erre azért van szükség, mert amikor egy élinkonzisztenciát eltávolítandó egy érték kikerül egy változó tartományából, az ehhez a változóhoz mutató éleknél új inkonzisztencia jöhet létre. Az AC-3, az élkonzisztencia teljes algoritmusa egy sort használ annak nyilvántartására, hogy mely élek inkonzisztenciáját kell még ellenőriznie (lásd 5.7. ábra). Minden egyes (Xi, Xj) élet sorban egyenként levesszük a tennivalók listájáról és ellenőrizzük; ha pedig Xi tartományának bármely változóját törölni kell, akkor minden Xi -be mutató (Xk, Xi) élet visszateszünk ellenőrzésre a sorba. Az élkonzisztencia-ellenőrzés komplexitása az alábbiak szerint vizsgálható: egy bináris kényszerkielégítési problémában legfeljebb O(n2) él van; minden egyes (Xk, Xi) él csak d alkalommal kerülhet napirendre, mert Xi-ben összesen d törölhető érték van; egy él konzisztenciájának ellenőrzése elvégezhető O(d2) időben; tehát a legrosszabb esetben vett teljes idő O(n2d3). Ez ugyan lényegesen költségesebb, mint az előretekintő ellenőrzés, de az extra költség általában kifizetődik.[48]

Mivel a kényszerkielégítési problémák speciális esetként tartalmazzák a 3SAT-ot, ezért nem várhatjuk, hogy polinom idejű algoritmust találunk annak eldöntésére, hogy egy adott kényszerkielégítési probléma konzisztens-e. Ebből arra következtethetünk, hogy az élkonzisztencia nem tár fel minden lehetséges inkonzisztenciát. Például az 5.1. ábrán az {NyA = vörös, ÚDW = vörös} részleges hozzárendelés inkonzisztens, de az AC-3 nem találja meg. Definiálható a terjesztés erősebb formája is, amit k-konzisztenciának (k-consistency) nevezünk. Egy kényszerkielégítési probléma akkor k-konzisztens, ha bármely k – 1 változóból álló halmaz és ezen változók bármely konzisztens hozzárendelése esetén mindig lehet a k-adik változónak konzisztens értéket találni. Az 1-konzisztencia például azt jelenti, hogy mindegyik individuális változó önmagában véve is konzisztens; ezt csomópont-konzisztenciának (node consistency) is nevezik. A 2-konzisztencia ugyanaz, mint az élkonzisztencia. A 3-konzisztencia azt jelenti, hogy egymás melletti változók bármely párja mindig kiterjeszthető egy szomszédos változóra; ezt útvonal-konzisztenciának (path consistency) is nevezik.
Egy gráf erősen k-konzisztens akkor, ha k-konzisztens, valamint (k – 1)-konzisztens, (k – 2)-konzisztens és így tovább le egészen az 1-konzisztenciáig. Tegyük fel most, hogy van egy n csomópontból álló kényszerkielégítési problémánk, és tegyük erősen n-konzisztenssé (azaz k-konzisztenssé k = n esetében). Ekkor visszalépés nélkül megoldhatjuk a problémát. Először egy konzisztens értéket választunk X1 számára. Ezután garanciánk van arra, hogy tudunk X2 számára értéket választani, mert a gráf 2-konzisztens, X3 számára, mert a gráf 3-konzisztens és így tovább. Minden egyes Xi változó esetén csak d értéket kell ellenőriznünk a tartományból, hogy egy X1 ,..., Xi–1-gyel konzisztens értéket találjunk. Garanciánk van tehát arra, hogy O(nd) időben megoldást találunk. Persze semmit sem adnak ingyen: az n-konzisztenciát biztosító bármely algoritmus legrosszabb esetben n-ben exponenciális lesz.
Az n-konzisztencia és az élkonzisztencia között egy széles köztes mező húzódik: az erősebb konzisztencia-ellenőrzések futtatása tovább fog tartani, de több eredménnyel jár az elágazási tényező csökkentésében és az inkonzisztens részleges hozzárendelések felderítésében. Ki lehet számolni a legkisebb olyan k értéket, melyre a k-konzisztencia ellenőrzésének futtatása visszalépés nélküli problémamegoldást tesz lehetővé (lásd 5.4. alfejezet), de ez gyakran nem célszerű. A legmegfelelőbb konzisztencia-ellenőrzési szint kiválasztása valójában leginkább empirikus tudomány.
A kényszerek bizonyos típusai gyakran fordulnak elő a valós problémákban és speciális célú algoritmusokkal jóval hatékonyabban kezelhetők, mint az eddig leírt általános célú módszerekkel. Például a MindKül kényszer azt állítja, hogy a benne szereplő öszszes változóknak mind különböző értéket kell felvennie (ahogy a betűrejtvényes példában láttuk). A MindKül kényszer inkonzisztencia-ellenőrzésére egy egyszerű módszer az, hogy ha m változó szerepel a kényszerben, és ha ezeknek együttesen n különböző értéke lehet, akkor m > n esetén a kényszert nem lehet kielégíteni.
Ez a következő egyszerű algoritmushoz vezet: először vegyünk ki a kényszerből minden változót, amelynek egyelemű tartománya van, és vegyük ki ezeknek a változóknak az értékeit a megmaradó változók tartományaiból. Ismételjük ezt a lépést mindaddig, amíg van ilyen változónk. Ha bármely ponton egy üres tartomány jön létre, vagy több változónk marad, mint értékünk a tartományban, akkor egy inkonzisztenciát derítettünk fel.
Ezt a módszert használhatjuk arra, hogy az 5.1. ábra {NyA = vörös, ÚDW = vörös} részleges hozzárendelésében észrevegyük az inkonzisztenciát. Figyeljünk fel arra, hogy a DA, az ÚT és a Q változók lényegében egy MindKül kényszerrel vannak összekötve, mert mindegyik párnak különböző színűnek kell lennie. Miután alkalmaztuk az AC-3-at a részleges hozzárendelésre, az egyes változók tartománya a {zöld, kék} tartományra szűkült le. Azaz három változónk van és csupán két színünk, tehát megszegtük a MindKül kényszert. Tehát a magasabb szintű kényszerekre alkalmazott egyszerű konzisztencia-ellenőrzések néha hatékonyabbak, mintha az ekvivalens bináris kényszerek halmazára vizsgáltuk volna az élkonzisztenciát.
A legfontosabb magasabb rendű kényszer talán az erőforráskényszer (resource constraint), amit néha legfeljebb kényszernek is neveznek. Jelölje például PA1, ..., PA4 rendre négy feladathoz hozzárendelt személyzet számát. Azt a kényszert, miszerint öszszesen nem lehet 10-nél több embernek feladatot adni, így írhatjuk fel: legfeljebb(10, PA1, PA2, PA3, PA4). Az inkonzisztenciát egyszerűen ki lehet mutatni az aktuális tartományok minimális értékeinek összegzésével: ha például mindegyik változó tartománya a {3, 4, 5, 6}, akkor a legfeljebb kényszert nem lehet kielégíteni. A konzisztenciát azáltal is érvényesíthetjük, hogy töröljük bármely tartomány maximális értékét, amely nem konzisztens az összes többi tartomány minimális értékével. Így ha példánkban mindegyik változónak {2, 3, 4, 5, 6} a tartománya, akkor az 5 és a 6 értékeket mindegyik tartományból törölni lehet.
A nagy erőforrás-korlátozott egész értékű problémáknál – ilyenek például az emberek ezreit és járművek százait mozgató logisztikai problémák – általában nem tehető meg az, hogy mindegyik változó tartományát egy nagy egészhalmazzal ábrázoljuk, majd ezt a halmazt a konzisztencia-ellenőrző módszerek segítségével fokozatosan csökkentjük. Ehelyett a tartományokat az alsó és a felső határaikkal ábrázoljuk, és határterjesztés segítségével kezeljük. Tegyük fel például, hogy két repülőjárat van, a 271-es és a 272-es, amelyekre a repülőgépek kapacitása rendre 165 és 385. A repülőjárat utasszámának kezdeti tartománya tehát
Járat271 ∈ [0, 165] és Járat272 ∈ [0, 385]
Tegyük fel most, hogy van egy külön korlát, miszerint a két járatnak együtt 420 embert kell szállítania. Járat271 + Járat272 ∈ [420, 420]. A határkényszereket terjesztve a tartományokat a következőkre csökkentjük:
Járat271 ∈ [35, 165] és Járat272 ∈ [225, 385]
Akkor nevezünk egy kényszerkielégítési problémát határkonzisztensnek, ha minden X változóra ennek a változónak mind az alsó, mind a felső határértékére található minden Y változóhoz olyan érték, amely kielégíti az X és Y közti kényszereket. Ezt a fajta kényszerterjesztést (bound propagation) széles körben használják a gyakorlati kényszerkielégítési problémák során.
Az 5.3. ábra VISSZALÉPÉSES-KERESÉS algoritmusa egy elég egyszerű intézkedést alkalmaz akkor, amikor egy keresési ág meghiúsul: visszalép az előző változóra, és megpróbál számára egy másik értéket találni. Ezt időrendi visszalépésnek (chronological backtracking) nevezik, mert a legutolsó döntési pontot keresi fel újra. Ebben az alrészben látni fogjuk, hogy adódik erre sokkal jobb módszer is.
Nézzük meg, mi történik, amikor az egyszerű visszalépéses algoritmust az 5.1. ábrán látható problémára alkalmazzuk rögzített változósorrenddel (Q, ÚDW, V, T, DA, NyA, ÚT). Tegyük fel, hogy már létrehoztuk a {Q = vörös, ÚDW = zöld, V = kék, T = vörös} hozzárendelést. Amikor a következő változóval, DA-val próbálkozunk, azt látjuk, hogy mindegyik érték sérti a kényszert. Visszalépünk T-re, és egy új színt keresünk Tasmania számára. Ez nyilvánvalóan butaság: Tasmania átszínezése nem oldja meg a Dél-Ausztráliával kapcsolatos problémát.
A visszalépéses megközelítés intelligens alkalmazása lenne, ha ahhoz a változóhalmazhoz mennénk vissza, amely a meghiúsulást okozta. Ezt a halmazt konfliktushalmaznak (conflict set) nevezik; esetünkben a DA-hoz tartozó konfliktushalmaz a {Q, ÚDW, V}. Általános esetben egy X változó konfliktushalmaza a korábban értéket kapott változók egy halmaza, melyeket X-hez kényszerek kötnek. A visszaugrás (backjumping) a konfliktushalmaz-beli legutolsó változóhoz lép vissza; esetünkben a visszaugrás átugorná Tasmaniát, és V számára próbálna új értéket keresni. Ezt egyszerű implementálni a VISSZALÉPÉSES-KERESÉS olyan módosításával, hogy az összegyűjtse a konfliktushalmazt, miközben hozzárendelhető értékeket keres. Ha nem talál ilyen értéket, akkor a konfliktushalmaz legutolsó elemét kell visszaadnia (a meghiúsulás jelzésével együtt).
Az éles szemű olvasónak feltűnhetett, hogy az előrenéző ellenőrzés a konfliktushalmazt minden külön munka nélkül előállíthatja: mindig amikor az előrenéző ellenőrzés X egy hozzárendelésén alapulva Y tartományából kitöröl egy elemet, X-et hozzá kell adnia Y konfliktushalmazához. Ezenkívül még minden esetben, amikor az utolsó értéket törli Y tartományából, az Y konfliktushalmazában szereplő változókat hozzá kell adnia X konfliktushalmazához. Ezek után mihelyt Y-hoz jutunk, már azonnal ismerni fogjuk, hogy hova lépjünk vissza, ha erre szükség van.
Fontos
A sasszemű olvasónak valami furcsaság is feltűnhetett: a visszaugrás akkor következik be, amikor egy tartomány minden értéke konfliktusban van az aktuális hozzárendelésekkel, de az előrenéző ellenőrzés felismeri ezt az eseményt, és megakadályozza, hogy valaha is ilyen csomóponthoz jussunk! Valóban, meg lehet mutatni, hogy a visszaugrás által levágott minden ágat az előrenéző ellenőrzés is levágja. Tehát az egyszerű visszaugrás redundáns az előrenéző ellenőrzés során, vagy pontosabban szólva, egy olyan keresésnél, amely erősebb konzisztencia-ellenőrzést, például MAC-ot használ.
Az előző bekezdés megfigyelése ellenére a visszaugrás mögötti ötlet továbbra is használható marad: lépjünk vissza a hiba helyére. A visszaugrás akkor veszi észre a kudarcot, amikor egy változó értéktartománya üressé válik, de sok esetben egy ág már sokkal korábban levágásra lett ítélve. Tekintsük ismét az {NyA = vörös, ÚDW = vörös} részleges hozzárendelést (amelyik, korábbi megjegyzéseink értelmében, inkonzisztens). Tegyük fel, hogy a T = vörös-t próbáljuk, majd az ÚT, Q, V, DA-kra alkalmazzunk hozzárendeléseket. Tudjuk, hogy az utóbbi négy változó esetén semmilyen hozzárendelés sem lesz jó, így végül ÚT próbálgatásánál kifogyunk az értékekből. A kérdés most az, hogy hova lépjünk vissza? A visszaugrás nem fog működni, mert ÚT-nek igenis van az előző hozzárendelésekkel konzisztens értéke: ÚT esetén nincsen teljes konfliktushalmaz a megelőző változók között, amely felelős lenne a kudarcért. Tudjuk azonban, hogy a négy változó, ÚT, Q, V, és DA együttvéve a megelőző változók egy halmaza miatt hiúsul meg, és ezek azok a változók, amelyek közvetlenül konfliktusban állnak a kérdéses néggyel. Ennek alapján ÚT konfliktushalmazának egy mélyebb megértéséhez jutottunk: a konfliktushalmaz a megelőző változók azon halmaza, ami bármely következő változóval együtt felelős ÚT konzisztens megoldásának kudarcáért. Esetünkben ez a halmaz az NyA és az ÚDW, tehát az algoritmusnak ÚDW-hez kell visszalépnie átugorva Tasmaniát. A konfliktushalmaz ilyen definíciójára támaszkodó visszaugrási algoritmust nevezzük konfliktusvezérelt visszaugrásnak (conflict-directed backjumping).
Magyarázatot kell most adnunk arra, hogy miként lehet kiszámítani ezeket az újfajta konfliktushalmazokat. A módszer valójában nagyon egyszerű. Egy keresési ág „terminálási” kudarca mindig azért következik be, mert egy változó tartománya kiürül, ennek a változónak pedig egy szokásos konfliktushalmaza van. Példánkban DA hiúsul meg, és konfliktushalmaza (mondjuk) az {NyA, ÚT, Q}. Visszaugrunk Q-ra, és Q beépíti saját közvetlen konfliktushalmazába (ami az {ÚT, ÚDW}) DA konfliktushalmazát (leszámítva persze Q-t magát), és így előáll az {NyA, ÚT, ÚDW} konfliktushalmaz. Azaz Q-tól számítva tovább már nincsen megoldás feltételezve {NyA, ÚT, ÚDW} korábbi hozzárendeléseit. Tehát visszalépünk ÚT-re, amelyik a legutóbbi ezek közül. ÚT felveszi {NyA, ÚT, ÚDW} – {ÚT}-t a saját közvetlen konfliktushalmazába, {NyA}-ba, és előáll az {NyA, ÚDW} konfliktushalmaz (ahogy az előző bekezdésben állítottuk). Foglaljuk össze az eddig mondottakat: jelölje Xj az aktuális változót és conf(Xj) a saját konfliktushalmazát. Ha Xj minden lehetséges értéke meghiúsul, ugorjunk vissza a conf(Xj)-beli legutolsó Xi értékre és legyen
conf(Xi) ← conf(Xi) ∪ conf(Xj) – {Xi}
A konfliktusvezérelt visszaugrás a keresési fa megfelelő helyére visz vissza, de nem akadályozza meg, hogy ugyanazt a hibát elkövessük a fa egy másik ágán. A kényszertanulás (constraint learning) a konfliktusból kiemelt új kényszer megtanulásával módosítja a kényszerkielégítési problémát.
[48] A Mohr és Henderson (Mohr és Henderson, 1986) bemutatta AC-4 algoritmus O(n2d2) alatt fut. (Lásd 5.10. feladat.)

