A matematikusok egy vektort egy vektortérelemként definiálnak. Mi azonban konkrétabb definíciót fogunk használni. Egy vektor az értékek egy rendezett szekvenciája. A kétdimenziós térben például olyan vektoraink vannak, mint: x = 〈3, 4〉 és y = 〈0, 2〉. A szokásos konvencióhoz folyamodunk vastagon szedett betűket használva a vektorneveknek, bár egyes szerzők a nevek fölé nyilat vagy vonalat húznak: 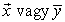. Egy vektor elemeire indexekkel lehet hivatkozni: z = 〈z₁, z₂, …, z_n〉.

A vektorokon értelmezett két alapvető művelet a vektorok összeadása és egy skalárral való szorzása. Az x + y vektorösszeadás az elemenkénti összegzés: x + y = 〈3 + 0, 4 + 2〉 = 〈3, 6〉. A skalárszorzás mindegyik elemet egy konstans értékkel szorozza be: 5x = 〈5 × 3, 5 × 4〉 = 〈15, 20〉.

Egy vektor hosszát az |x| jelöli, amelynek értéke egyenlő a vektor elemeinek négyzetösszegéből vett négyzetgyökével: 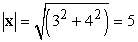. Két vektor skalárszorzata, x · y a megfelelő vektorelemek szorzatának összege, azaz 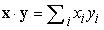, vagy konkrét esetünkben x · y = 3 × 0 + 4 × 2 = 8.

A vektorokat sokszor egy n-dimenziós euklideszi tér irányított vonalszakaszainak (nyilaknak) képzeljük. Ekkor a vektorösszeadás annak felel meg, mintha az egyik vektor kezdő pontját a másik vektor végpontjához illesztenénk, az x · y skalárszorzat viszont |x||y|cosθ-vel lesz egyenlő, ahol θ az x és az y közötti szög.

Egy mátrix az értékek négyszögletes elrendezése sorokba és oszlopokba. Itt egy 3 × 4 méretű m mátrixot látunk:

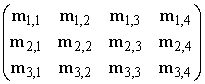
Az m_i,j első indexe a sort, a második az oszlopot jelöli. Programozási nyelvekben m_i,j-t gyakran m[i,j], vagy m[i][j]-nek írják.

Két mátrix összegét a megfelelő elemek összeadásával definiáljuk: (m + n)_i,j = m_i,j + n_i,j. (Az összeg különböző méretű m és n mátrixokra nincs definiálva.) Egy mátrixnak egy skalárral történő szorzatát szintén definiálhatjuk: (cm)_i,j = cm_i,j. A mátrixszorzat (két mátrix szorzata) már bonyolultabb. Az mn szorzat csak akkor definiált, ha az m mátrix a × b, az n mátrix pedig b × c méretű (azaz a második mátrixnak annyi sora van, mint amennyi oszlopa az első mátrixnak). Az eredmény egy a × c méretű mátrix. Ez azt jelenti, hogy a mátrixszorzat nem kommutatív: általánosságban mn ≠ nm. Ha a mátrixok megfelelő méretűek, akkor az eredmény:

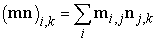
Az I egységmátrix I_i,j elemei egységnyiek, ha i = j, különben nullák. Az egységmátrix tulajdonsága, hogy mI = m, minden m-re. Az m transzponáltját, m^T-t, megkapjuk, ha az m sorait és oszlopait felcseréljük, formálisan: .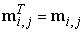

A mátrixokat lineáris egyenletrendszerek megoldására a Gauss–Jordan-eliminációs (Gauss–Jordan elimination) algoritmussal használjuk, ami egy O(n³) komplexitású algoritmus. Tekintsünk az alábbi egyenletrendszert, amelynek x, y és z megoldására vagyunk kíváncsiak:

+2x + y – z = 8

–3x – y + 2z = –11

–2x + y + 2z = –3

Ezt az egyenletrendszert kifejezhetjük mátrixos formában is:

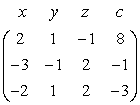
Itt az x y z c nem része a mátrixnak, csak emlékeztetőül szolgál. Tudjuk, hogy ha egy egyenlet mindkét oldalát egy konstanssal megszorozzuk, vagy ha két egyenletet egymáshoz hozzáadunk, akkor szintén egy érvényes egyenlethez jutunk el. A Gauss– Jordan-elimináció ezeket a lépéseket ismételten alkalmazza úgy, hogy először az első változót (az x-et) elimináljuk, az elsőt kivéve az összes egyenletből, majd folytatjuk minden i-re, az i-edik változót minden egyenletből eliminálva, az i-edik egyenletet kivéve. Az x-et a második egyenletből úgy elimináljuk, hogy az első egyenletet 3/2-vel megszorozzuk, az eredményt pedig a második egyenlethez hozzáadjuk. Ezzel az alábbi mátrixhoz jutunk el:

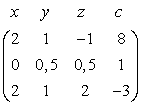
Folytatjuk így eliminálva az x-et, az y-t és a z-t, míg végül a:

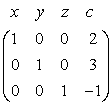
mátrixot kapjuk, amely jelzi, hogy a megoldás x = 2, y = 3, z = –1. (Próbálja ki!)