21.5. Stratégiakeresés
A megerősítéses tanulással kapcsolatos, utolsó általunk tárgyalt megközelítés stratégiakeresés (policy search) néven ismert. Bizonyos értelemben a stratégiakeresés a legegyszerűbb a fejezet összes módszere közt. Az alapötlet annyi, hogy engedjük változni a stratégiát, amíg javul, és utána állítsuk le a változást.
A vizsgálatot kezdjük magával a stratégiával. Emlékezzünk vissza, hogy a π stratégia egy olyan függvény, amely állapotokat képez le cselekvésekre. Mi elsősorban olyan paraméterezet π stratégiák vizsgálatában vagyunk érdekeltek, amelyeknek sokkal kevesebb paramétere van, mint ahány állapot található az állapottérben (éppúgy, mint az előző alfejezetben). Például paraméterezett Q-függvényekkel reprezentálhatjuk a π stratégiát, egy-egy Q-függvényt rendelve minden cselekvéshez, és azt a cselekvést választjuk, amely a legnagyobb jósolt értéket adja:
Fontos
Minden egyes Q-függvény lehet a θ paraméterek lineáris függvénye, mint a (21.9) egyenletben, vagy lehet nemlineáris függvény, mint például egy neurális háló. A stratégiakeresés ezek után a θ paramétereket változtatja oly módon, hogy javítsa a stratégiát. Vegyük észre, hogy ha a stratégiát Q-függvényekkel reprezentáljuk, akkor a stratégiakeresés egy Q-függvény tanulási eljárást eredményez. Ez a folyamat azonban nem azonos a Q-tanulással! A függvényapproximációt használó Q-tanulásban az algoritmus egy olyan θ-t keres, amelyre a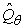 
„közel” van Q*-hoz, az optimális Q-függvényhez. A stratégiakeresés ezzel szemben olyan θ-t keres, amely jó működést eredményez, az eredményül kapott értékek alapvetően eltérhetnek.[217] Egy másik nyilvánvaló példa a két dolog különbségére az az eset, amikor a π(s) stratégiát úgy számítjuk, hogy 10 lépés mélységben előretekintő keresést végzünk egy közelítő 
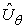hasznosságfüggvény alapján. A jó eredményt adó θ messze lehet attól, amely az 
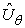-t az igazi hasznosságfüggvényhez hasonlóvá teszi.
A (21.13) egyenletben bemutatott stratégiareprezentáció egyik problémája, hogy diszkrét cselekvések esetén a stratégia a paraméterek nemfolytonos függvénye.[218] Azaz lesznek olyan θ értékek, amelyeknél végtelen kis változás a θ-ban azt eredményezi, hogy a stratégia egyik cselekvésről a másikra vált. Ez azt is jelenti, hogy a stratégia értéke is változhat nemfolytonos módon, ami nehézzé teszi a gradiensalapú eljárások alkalmazását. Emiatt a stratégiakeresési eljárások gyakran használják a πθ(s, a) sztochasz-tikus stratégia (stochastic policy) reprezentációt, amely az s állapotban az a cselekvés választásának valószínűségét specifikálja. Egy népszerű reprezentáció a szoftmax függvény (softmax function):
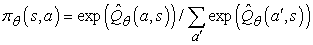
A szoftmax függvény közel determinisztikussá válik, ha az egyik cselekvés sokkal jobb, mint a többi, de mindig differenciálható θ szerint; így a stratégia értéke (amely folytonos módon függ a cselekvésválasztási valószínűségtől) differenciálható függvénye lesz θ-nak.
Nézzünk most módszereket a stratégia javítására. Kezdjük a legegyszerűbb esettel: determinisztikus stratégia, determinisztikus környezetben. Ebben az esetben a stratégia értékelése triviális: egyszerűen végrehajtjuk a stratégiát, és megfigyeljük az összegyűjtött jutalmat, ez adja számunkra a stratégia értékét (policy value), ρ(θ)-t. A stratégia javítása ezek után egy standard optimalizációs probléma, ilyeneket a 4. fejezetben tárgyaltunk. Követhetjük a stratégiagradiens (policy gradient) vektort, ∇θ ρ(θ)-t, feltéve, hogy ρ(θ) differenciálható. Másik lehetőség, ha az empirikus gradienst (empirical gradient) követjük hegymászó módszerrel – azaz kiértékeljük a stratégiát minden egyes paraméter kis megváltozása esetére. A szokásos feltételek esetén ez a stratégiatér egy lokális optimumához fog konvergálni.
Ha a környezet (vagy a stratégia) sztochasztikus, akkor a helyzet nehezebbé válik. Tegyük fel, hogy hegymászó módszert próbálunk alkalmazni, ami azt kívánja, hogy összehasonlítsuk ρ(θ)-t ρ(θ + Δθ)-val valamilyen kis Δθ esetén. Az a probléma, hogy a teljes jutalom nagyon nagyokat változhat kísérletről kísérletre, így a kisszámú kísérletből számított stratégiaérték nagyon megbízhatatlan lesz – két ilyen becslés összehasonlítása pedig még megbízhatatlanabb. Egy lehetséges megoldás, ha egyszerűen sok kísérletet futtatunk le, és a minta variancájával mérjük, hogy elegendő kísérletet futtattunk-e már ahhoz, hogy megbízhatóan jelezni tudjuk a ρ(θ) javításának irányát. Sajnálatos módon ez sok valós probléma esetén nem praktikus, mert az egyes kísérletek drágák, időigényesek és esetleg veszélyesek lehetnek.
A πθ(s, a) sztochasztikus stratégia esetén lehetőségünk van arra, hogy a θ-ban végrehajtott kísérletek eredményei alapján a ∇θ ρ(θ) gradiens torzítatlan becslését állítsuk elő θ-ban. Az egyszerűség kedvéért a becslést arra az egyszerű esetre vezetjük le, amikor nem szekvenciális környezetben közvetlenül az s0 startállapotbeli cselekvés után megkapjuk a jutalmat. Ebben az esetben a stratégiaérték egyszerűen a jutalom várható értéke, tehát:
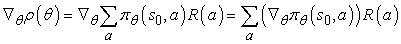
Most egy egyszerű trükköt alkalmazunk, hogy ezt az összegzést approximálni tudjuk a πθ(s, a) által meghatározott valószínűség-eloszlásból generált mintákkal. Tegyük fel, hogy összesen N kísérletünk van, és a j-edik kísérletben az aj cselekvést választottuk. Ekkor
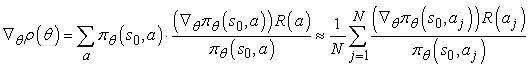
Tehát a stratégia igazi gradiensét egy szummával közelítettük, ahol a tagok az egyes kísérletek cselekvésválasztási valószínűségeinek gradiensét tartalmazzák. A szekvenciális esetre ez a következőképp általánosítható:
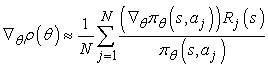
minden egyes bejárt s állapotra. Itt aj a j-edik kísérlet során az s állapotban választott cselekvés, és Rj(s) a j-edik kísérlet során az s állapotból kiindulva gyűjtött összes jutalom. Az eredményül kapott algoritmust REINFORCE-nak nevezték el (Williams, 1992). Rendszerint sokkal hatékonyabb, mint a minden egyes θ-ban sok kísérletet használó hegymászó eljárás. Viszont sajnos még mindig sokkal lassabb annál, mint amire szükségünk lenne.
Fontos
Vizsgáljuk a következő feladatot: adott két blackjack[219] program, döntsük el, hogy melyik a jobb! Egyik lehetőség, ha egy közös „bank” ellen játszatjuk őket egy adott számú kártyaleosztásban, és megnézzük, hogy melyik nyert többet. Ezzel az a probléma – mint láttuk –, hogy mindegyik program nyereségei nagy fluktuációt fognak mutatni annak függvényében, hogy milyen lapokat kapott. Egy kézenfekvő megoldás erre, ha előre generálunk egy sor leosztást, egy leosztáshalmazt. Ezzel elkerüljük a különböző kártyaleosztások okozta mérési hibát. Ez a PEGASUS algoritmus ötletének alapja (Ng és Jordan, 2000). Az algoritmus olyan területeken alkalmazható, ahol rendelkezésünkre áll egy szimulátor, ezáltal a „véletlen” kísérlet kimenetelek megismételhetővé válnak. Az algoritmus N véletlen számsorozatot generál előre, mindegyik felhasználható arra, hogy egy tetszőleges stratégia alapján kísérletet futtassunk vele. A stratégiakeresést úgy hajtjuk végre, hogy mindegyik stratégiajelöltet az alapján értékelünk, hogy ugyanazt a véletlen sorozat halmazt használja a kísérletek kimeneti értékeinek meghatározásához. Megmutatható, hogy az összes stratégia értékének jó becsléséhez szükséges véletlen sorozatok száma csak a stratégiatér komplexitásától függ, és egyáltalán nem függ a mögöttes terület komplexitásától. A PEGASUS algoritmussal számos területen (például az autonóm helikoptervezetés területén) több hatékony stratégiát fejlesztettek ki (lásd 21.10. ábra).
21.10. ábra - Időben eltolt képek egymásra másolása útján kapott eredő kép, amelyen egy nagyon bonyolult „körberepülés orral a kör középpontja fele” manővert hajtanak végre. A helikoptert egy Pegasus stratégiakereső algoritmussal fejlesztett stratégiával vezérlik. Egy szimulátormodellt fejlesztettek a valós helikopter egyes vezérlési beavatkozásokra adott válaszainak vizsgálatára. Ezek után egész éjszaka futtatták az algoritmust a szimulátoron. Egy sor vezérlőt fejlesztettek ki különböző manőverekre. Minden esetben, amikor távirányítást használtak, messze jobb volt az eredmény, mint a képzett humán pilótáké. (A képet Andrew Ng engedélyével közöljük.)
