20.6. Kernelgépek
A neurális hálók tárgyalása után maradt egy dilemmánk. Az egyrétegű hálóknak nagyon egyszerű és hatékony tanulási algoritmusuk van, de nagyon korlátozott a kifejezőképességük, csupán lineáris döntési határokat képesek megtanulni a bemeneti térben. Másrészt a többrétegű hálók sokkal kifejezőbbek – általános nemlineáris függvényeket képesek reprezentálni –, de a rengeteg lokális minimum jelenléte, illetve a sokdimenziós súlytér miatt nagyon nehéz a tanításuk. Ebben az alfejezetben egy relatíve új tanulómódszer családot fedezünk fel, az úgynevezett szupport vektor gépeket (support vector machines, SVM), vagy általánosabban a kernelgépeket (kernel machines). Bizonyos fokig a kernelgépek a két oldal legjobb tulajdonságait egyesítik. Azaz ezek a módszerek hatékony tanítási algoritmusokat alkalmaznak, ugyanakkor képesek bonyolult, nemlineáris függvények reprezentálására.
A kernelgépek teljes mélységű tárgyalása meghaladja ennek a könyvnek a kereteit, de a fő gondolatot egy példán keresztül illusztráljuk. A 20.27. (a) ábra egy kétdimenziós bemeneti teret mutat, amelyet az x = (x1, x2) attribútumok írnak le. A pozitív példák (y = +1) egy kör alakú rész belsejében, a negatív példák (y = –1) azon kívül helyezkednek el. Nyilvánvaló, hogy a probléma megoldására nem létezik lineáris szeparátor. Tegyük fel, hogy valamilyen számított tulajdonságok segítségével új formára hozzuk a példákat – azaz az összes bemeneti x vektort leképezzük a tulajdonságértékekből formált új, F(x) vektorra. A példában használjuk a következő három tulajdonságot:

Rövidesen látni fogjuk, hogy honnan vesszük ezeket a tulajdonságokat, de most csak nézzük meg azt, hogy mi is történt. A 20.27. (b) ábra mutatja az adatokat az új, a tulajdonságok által definiált háromdimenziós térben: ebben a térben lineárisan szeparálhatók! Ez a jelenség eléggé általános: ha az adatokat megfelelően sokdimenziós térbe képezzük le, akkor mindig lineárisan szeparálhatók lesznek. Itt mi csak három dimenziót használtunk,[208] de ha N pontunk van – akkor speciális esetek kivételével –, egy N – 1 vagy ennél magasabb dimenziós térben a pontok mindig lineárisan szeparálhatók lesznek (lásd 20.21. feladat).
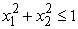 valódi elválasztó határt is bejelöltük. (b) Ugyanazok az adatok az
valódi elválasztó határt is bejelöltük. (b) Ugyanazok az adatok az 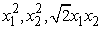 háromdimenziós térbe való leképezés után. Az (a) ábrán látható kör alakú döntési határ a háromdimenziós térben lineáris döntési felületbe ment át.
háromdimenziós térbe való leképezés után. Az (a) ábrán látható kör alakú döntési határ a háromdimenziós térben lineáris döntési felületbe ment át.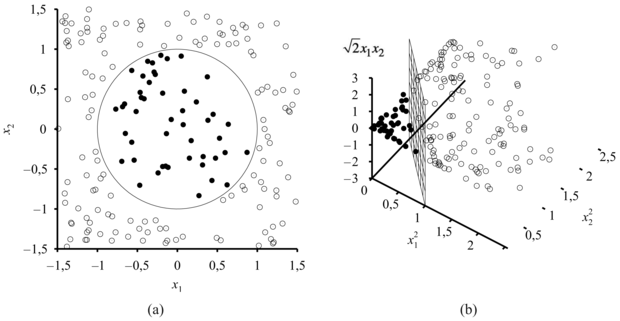
Ennyi az egész? Egyszerűen létrehozunk egy nagy halom számított tulajdonságot, és a megfelelő sokdimenziós térben megkeressük a lineáris szeparátort? Sajnálatos módon nem ilyen egyszerű. Emlékezzünk, hogy a d dimenziós térben a lineáris szeparátort egy d paraméteres egyenlet határozza meg, így aztán az a veszély fenyeget, hogy ha d ≈ N (ahol N az adatpontok száma), akkor könnyen túlilleszkedhetünk az adatokra. (Ez ahhoz hasonló, mint amikor egy magas fokszámú polinommal túlillesztünk adatokat, ahogy ezt a 18. fejezetben tárgyaltuk.) Ezen okból a kernelgépek rendszerint az optimális lineáris szeparátort találják meg. Azt nevezzük optimálisnak, amelynek legnagyobb a tartaléka (margin): a lineáris szeparátor és a pozitív példák között az egyik oldalon, illetve a lineáris szeparátor és a negatív példák között a másikon. (Lásd 20.28. ábra.) A számítógépes tanulás elmélet módszereit (lásd 18.5. alfejezet) használva megmutatható, hogy ez a szeparátor az új példák robusztus általánosítására nézve nagyon jó tulajdonságokkal rendelkezik.
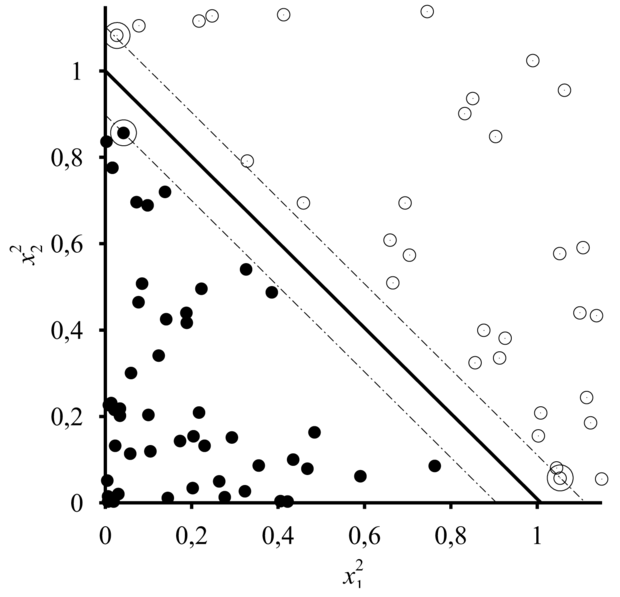
Hogyan találjuk meg ezt a szeparátort? Kiderül, hogy ez egy kvadratikus programozással (quadratic programming) megoldható optimalizálási feladat. Tegyük fel, hogy xi példáink vannak, az osztálybasorolásuk yi = ±1, és a bemeneti térben optimális szeparátort akarunk találni. Ekkor a megoldandó kvadratikus programozási feladat azon paraméterértékek megtalálása, amelyek az αi ≥ 0 és Σiαi yi = 0 korlátozó feltételek mellett maximálják a következő kifejezést:
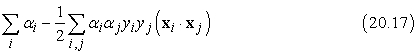
Fontos
Bár ennek a kifejezésnek a deriválása nem nagyon fontos pontja a történetnek, de azért van két lényeges tulajdonsága. Először is a kifejezésnek egyetlen, globális maximuma van, ami hatékonyan megtalálható. Másodszor az adatok kizárólag pontpárok skalárszorzataként jelennek meg a kifejezésben. Ez a második tulajdonság magára a szeparátorra is igaz, ha az optimális αi-ket kiszámítottuk, akkor:

Az ezen egyenlettel definiált optimális szeparátor utolsó fontos tulajdonsága az, hogy az egyes adatpontokkal asszociált αi súlyok mind nullák, kivéve a szeparátorhoz legközelebb eső pontokat – ezeket nevezzük szupport vektoroknak (support vector). (Azért nevezzük így őket, mert ők „tartják” a szeparáló síkot.) Mivel rendszerint jóval kevesebb szupport vektor van, mint adatpont, ezért az optimális szeparátort meghatározó tényleges paraméterszám rendszerint jóval kisebb N-nél.
Rendszerint nem várhatjuk el, hogy lineáris szeparátort találjunk az x bemeneti térben, de könnyen belátható, hogy a sokdimenziós F(x) tulajdonságtérben találhatunk lineáris szeparátorokat. Ennek érdekében a (20.17) egyenletben xi · xj-t egyszerűen kicseréljük F(xi) · F(xj)-re. Ez önmagában nem túlzottan figyelemre méltó – x kicserélése F(x)-re bármely tanuló algoritmusban elérné a kívánt hatást –, de a skalárszorzatnak van néhány érdekes tulajdonsága. Az F(xi) · F(xj) gyakran kiszámítható anélkül, hogy először kiszámítanánk minden pontra F-et. A (20.16) egyenlettel definiált háromdimenziós tulajdonságtér példánkban némi algebrai átalakításokkal megmutatható, hogy:
F(xi) · F(xj) = (xi · xj)2
Az (xi · xj)2 kifejezést kernelfüggvénynek (kernel function) nevezzük, és K(xi, xj)-vel jelöljük. A kernelgépek szempontjából ez egy olyan függvény, amely pontpárokra alkalmazható avégett, hogy valamilyen tulajdonságtérben kiszámítsuk a skalárszorzatukat. Ennek megfelelően újrafogalmazhatjuk állításunkat: a (20.17) egyenletben xi · xj-t egyszerűen kicserélve a K(xi, xj) kernelfüggvényre, a sokdimenziós F(x) tulajdonságtérben találhatunk lineáris szeparátorokat. Így a tanulást a sokdimenziós térben végezhetjük, de csupán kernelfüggvények értékét kell kiszámítanunk, nem kell az öszszes pontra a tulajdonságok teljes készletét kiszámítani.
Fontos
A következő lépés – aminek most már kézenfekvőnek kell lennie – az, hogy meglássuk, a K(xi, xj) = (xi · xj)2 kernelben nincs semmi különleges. Ez egy bizonyos sokdimenziós tulajdonságtérnek felel meg, de más kernelfüggvények más tulajdonságterekkel vannak kapcsolatban. A Mercer-tétel (1909) azt mondja ki, hogy bármely „ésszerű”[209] kernelfüggény megfelel valamilyen tulajdonságtérnek. Ez a tulajdonságtér még egész ártatlannak látszó kernelek esetén is nagyon nagy lehet. Például a K(xi, xj) = (1 + xi · xj)d polinomiális kernel (polynomial kernel) egy olyan tulajdonságtérnek felel meg, amelynek dimenziója d-ben exponenciális. Ha a (20.17) egyenletben ilyen kerneleket használunk, akkor hatékonyan kereshetünk lineáris szeparátorokat sok milliárd (vagy egyes esetekben végtelen) dimenziós terekben. Az eredményként kapott lineáris szeparátorokat visszavetítve az eredeti bemeneti térbe, a pozitív és negatív példákat elválasztó tetszőlegesen tekervényes, nemlineáris határfelületeket kaphatunk.
Említettük az előző részben, hogy a kernelgépek kiemelkedően teljesítenek a kézírásos számjegyek felismerésében, de gyorsan felhasználják őket más alkalmazásokhoz is, különösen olyanokhoz, ahol sok bemeneti tulajdonság van. Ennek a folyamatnak részeként számos új kernelt dolgoztak ki, amelyek karakterfüzérekre, fákra és más nemnumerikus adattípusokra alkalmazhatók. Az is megfigyelhető, hogy a kernelmódszer nemcsak optimális szeparátorok keresésére alkalmas, hanem bármely olyan algoritmusra, amely úgy átalakítható, hogy csak adatpontpárok skalárszorzatát használja, mint a (20.17), illetve (20.18) egyenlet. Amint ezt sikerült megtennünk, a skalárszorzat kicserélhető egy kernelfüggvényre, és elkészítettük az algoritmus kernelesített (kernelized) változatát. Ez az átalakítás többek közt a k-legközelebbi-szomszéd algoritmusra és a perceptron tanulásra is könnyen elvégezhető.

