15.1. Idő és bizonytalanság
A valószínűségi következtetésre szolgáló technikáinkat változatlan (static) világok esetén fejlesztettük ki, amelyekben minden egyes valószínűségi változónak egyetlen rögzített értéke van. Például egy gépkocsi javításánál feltesszük, hogy ami meghibásodott, az a diagnosztizálás alatt is hibás marad; a feladatunk a gépkocsi állapotának kikövetkeztetése a megfigyelt bizonyítékokból, amelyek szintén változatlanok maradnak.
Most vegyünk fontolóra egy másféle problémát: egy cukorbeteg páciens kezelését. Akárcsak a gépkocsijavítás esetén, rendelkezünk bizonyítékokkal: a jelenlegi inzulinadagok, az élelmiszer-bevitel, a vércukorszint mérésének eredményei és egyéb testi tünetek. A feladat a páciens jelenlegi állapotának értékelése, beleértve az aktuális vércukorszintet és inzulinszintet. Ezeknek az információknak az alapján az orvos (vagy a páciens) döntést hoz a páciens élelmiszer-beviteli és inzulinadagjáról.
A gépkocsijavítás esetétől eltérően, itt a probléma dinamikai vonatkozásai alapvetőek. A vércukorszintek és méréseik idővel gyorsan változhatnak, amit befolyásol a páciens aktuális élelmiszer-bevitele és inzulinadagja, az anyagcsere aktivitása, a napszak és egyéb tényezők. Ahhoz, hogy a bizonyítékok időbeli alakulásából a jelenlegi állapotot megbecsüljük, és egy kezelés kimenetelét megjósoljuk, modelleznünk kell ezeket a változásokat.
Ugyanezek a szempontok számos más esetben is jelentkeznek, egy nemzet gazdasági aktivitásának közelítő és részleges statisztikák alapján történő követésétől, beszédszekvenciák zajos és többértelmű akusztikai mérésekből történő megértéséig. Adódik a kérdés: hogyan lehet az ezekhez hasonló dinamikai helyzeteket modellezni?
Az alapvető megközelítés, amit követünk, hasonló a 10. fejezetben leírt szituációkalkulus alapjául szolgáló ötlethez: a változás folyamatát pillanatfelvételek sorozatának tekinthetjük, amelyek mindegyike egy adott pillanatban írja le a világ állapotát. Minden pillanatfelvétel vagy időpont (time slice) valószínűségi változók egy halmazát tartalmazza, amelyek némelyike megfigyelhető, némelyike pedig nem.
Az egyszerűség kedvéért a továbbiakban fel fogjuk tenni, hogy a változóknak ugyanaz a részhalmaza minden időpontban megfigyelhető (bár az elkövetkezőkben ez teljes mértékben sehol sem szükségszerű). A t időpillanatban nem megfigyelhető változók halmazának a jelölésére Xt-t fogjuk használni, és Et-t a megfigyelhető változók halmazának a jelölésére. A t időpontbeli megfigyelés Et = et az értékek valamely et halmazára.
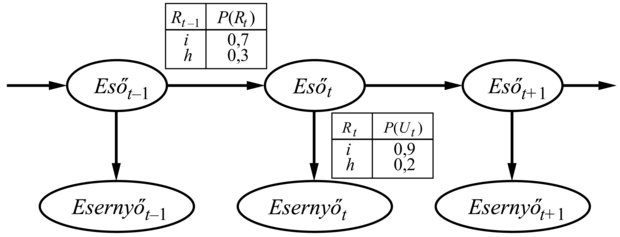
Gondoljuk át a következő leegyszerűsített példát: tegyük fel, hogy egy titkos, földalatti létesítmény biztonsági őrei vagyunk. Szeretnénk tudni, hogy vajon aznap esik-e, de a külvilághoz való egyetlen hozzáférésünket az jelenti, hogy reggelenként látjuk, hogy az igazgató esernyővel vagy esernyő nélkül jön be. Minden egyes t napon az Et halmaz így egyetlen bizonyítékváltozót tartalmaz, az Ut-t (van-e esernyő), és Xt az Rt-t, az egyetlen állapotváltozót tartalmazza (esik-e). Más problémákhoz változók nagyobb halmaza tartozhat. A cukorbetegség példájában a bizonyítékváltozók lehetnek a MértVércukort és a Pulzusszámt, és az állapotváltozók lehetnek a Vércukort és a Gyomortartalomt.[156]
Az időpontok közötti intervallum szintén problémafüggő. A cukorbetegség követésénél az alkalmas intervallum inkább egy óra, mint egy nap. Ebben a fejezetben általában egy rögzített véges intervallumot tételezünk fel, ami azt jelenti, hogy az időpillanatok egész számokkal felcímkézhetők. Feltesszük, hogy az állapotsorozat t = 0-nál kezdődik; és jelentéktelen okokból feltesszük, hogy a bizonyítékok t = 1-nél kezdenek beérkezni, és nem t = 0-nál. Így az esernyős világot az R0, R1, R2, ... állapotváltozók és az U1, U2, ... bizonyítékváltozók reprezentálják. Az a : b jelölést fogjuk használni az egészek a-tól b-ig tartó sorozatának jelölésére (a határokat beleértve), és Xa:b jelöli a változók megfelelő halmazát Xa-tól Xb-ig. Például U1:3 az U1, U2, U3 változóknak felel meg.
Egy adott problémánál az állapotváltozók és a bizonyítékváltozók halmazának meghatározása után a következő lépés a változók közötti függőségek megadása. Követhetnénk a 14. fejezetben megállapított eljárást, valahogyan sorrendezve a változókat, és kérdéseket feltéve az elődöktől való feltételes függetlenségre, adott szülői halmaz esetén. Egy nyilvánvaló választás, hogy a változókat a természetes idősorrendjük szerint sorrendezzük, mivel az ok általában megelőzi a hatást, és a változókat lehetőleg az ok-okozati sorrendjük szerint vesszük.
Azonban hamar beleütközhetünk egy akadályba: a változók halmaza nem korlátos, mivel minden időpontra tartalmazza az állapot- és bizonyítékváltozókat. Valójában ez két problémát is felvet: (1) korlátlan számú feltételes valószínűségi táblát kell megadnunk minden változóra, minden időpillanatban; (2) ezek korlátlan számú szülőt tartalmazhatnának.
Az első problémát megoldja annak feltételezése, hogy a világ állapotának a változásait egy stacionárius folyamat (stationary process) okozza – azaz egy változási folyamat, amit olyan törvények határoznak meg, amik maguk nem változnak az idővel. (Ne keverjük össze a stacionaritást a statikussággal: egy statikus folyamatban maga az állapot nem változik.) Az esernyős világban ekkor a P(Ut|Szülők(Ut)) feltételes valószínűség, hogy az esernyő feltűnik, minden t-re azonos. A stacionaritás feltevésénél ezért csak egy „reprezentatív” időpillanathoz tartozó változók feltételes valószínűségeit kell megadnunk.
A második problémát, a potenciálisan végtelen számú szülő kezelését, az úgynevezett Markov-feltétel (Markov assumption) elfogadása oldja meg – azaz, hogy a jelenlegi állapot a korábbi állapotoknak csak véges történetétől függ. Ennek a feltevésnek eleget tévő folyamatokat elsőként Andrei Markov orosz matematikus tanulmányozta részletesen. Ezeket a folyamatokat Markov-folyamatoknak (Markov processes) vagy Markov-láncoknak (Markov chains) neveznek. (A Markov-folyamatok feloszthatók aszerint, hogy az állapottér folytonos vagy diszkrét, illetve hogy az idő folytonos vagy diszkrét. Markov-láncoknak a diszkrét idejű és/vagy diszkrét állapotterű Markov-folyamatokat nevezik – a ford.) A Markov-folyamatok különböző jellemzőkkel rendelkezhetnek; a legegyszerűbb az elsőrendű Markov-folyamat (first-order Markov process), amelyben a jelenlegi állapot csak az előző állapottól függ, és nem függ egyetlen korábbitól sem. Máshogy fogalmazva, egyetlen állapot ismeretére van szükség, hogy a jövő a múlttól feltételesen független legyen az állapot ismeretében. A jelölésünket felhasználva, a megfelelő feltételes valószínűségi állítás azt mondja ki, hogy minden t-re
P(Xt|X0:t–1) = P(Xt|Xt–1) (15.1)
Így egy elsőrendű Markov-folyamatban az állapotok időbeli változását leíró szabályokat teljes mértékben tartalmazza a P(Xt|X1–t) feltételes eloszlás, amit az elsőrendű folyamat állapotátmenet-modelljének (transition model) nevezünk.[157] A 15.1. ábra elsőrendű és másodrendű Markov-folyamatokhoz tartozó Bayes-hálóstruktúrákat mutat.
15.1. ábra - (a) Egy elsőrendű Markov-folyamathoz tartozó Bayes-hálóstruktúra. A reprezentált Markov-folyamatban az állapotot az Xt változók definiálják. (b) Egy másodrendű Markov-folyamat.
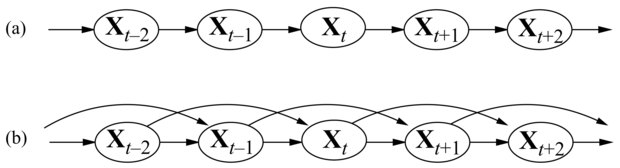
Az Xt állapotváltozók szüleinek a korlátozásán túl korlátoznunk kell az Et bizonyítékváltozók szüleit is. Tipikusan feltesszük, hogy a bizonyítékváltozók egy t időpillanatban csak az aktuális állapottól függnek:
P(Et|X0:t, E0:t–1) = P(Et|Xt) (15.2)
A P(Et|Xt) feltételes eloszlást érzékelő modellnek (sensor model) nevezik (vagy néha megfigyelési modellnek [observational model]), mivel leírja, hogy az „érzékelőket” – azaz a bizonyítékváltozókat – hogyan befolyásolja a világ aktuális állapota. Vegyük észre a függés irányát: a „nyíl” az állapottól az érzékelő értékére mutat, mivel a világ állapota okozza azt, hogy az érzékelők bizonyos értékeket vegyenek fel. Az esernyős világban például az eső okozza az esernyő feltűnését. (A következtetési folyamat természetesen a másik irányban halad; a modellezett függések iránya és a következtetés iránya közötti különbségtétel a Bayes-hálók egyik fő előnye.)
Az állapotátmenet-modellhez és az érzékelő modellhez még meg kell adnunk egy P(X0) a priori eloszlást a 0. időpontbeli állapotok felett. Ez a három eloszlás, kombinálva a (15.1) és a (15.2) egyenletekben megfogalmazott feltételes függetlenségi állításokkal, biztosítja számunkra a teljes együttes eloszlás meghatározását az összes változó felett. Bármely véges t-re azt kapjuk, hogy
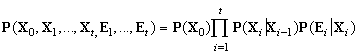
A függetlenségi állítások egy nagyon egyszerű Bayes-hálóstruktúrának felelnek meg, ami az egész rendszert leírja. A 15.2. ábrán látható a háló struktúrája az esernyős példa esetén, beleértve az állapotátmenet- és az érzékelő modellekhez tartozó feltételes eloszlásokat.
Az ábrán lévő struktúra elsőrendű Markov-folyamat feltételezésen alapul, mivel feltesszük, hogy az eső valószínűsége csak attól függ, hogy az előző nap esett-e. Egy ilyen feltevésnek a helyénvalósága magától a tárgyterülettől függ. Az elsőrendű Markov-feltétel kimondja, hogy az állapotváltozók az összes olyan információt tartalmazzák, amely a következő időpontbeli valószínűség-eloszlások megadásához szükséges. Néha ez a feltevés pontosan teljesül – például ha egy részecske véletlen bolyongást (random walk) végez az x tengelyen, ±1-gyel változtatva meg a pozícióját minden időpontban, ekkor az x koordinátát használva állapotként, egy Markov-lánc adódik. Gyakran a feltevés csak közelítő, mint amikor az eső jóslása csak az alapján történik, hogy esett-e az előző napon. Két lehetséges javítás létezik, ha a közelítés túlságosan pontatlannak bizonyul:
-
A Markov-folyamat rendjének a megnövelése. Például létrehozhatnánk egy másodrendű modellt, felvéve egy Esőt–2-t mint az Esőt szülőjét, ami lehet, hogy valamivel pontosabb predikciót adna (például Palo Altóban nagyon ritkán esik több mint két napig egyfolytában).
-
Az állapotváltozók halmazának megnövelése. Például felvehetnénk az Évszakt változót, hogy ez lehetővé tegye számunkra az esős évszakok történeti feljegyzéseinek beépítését, vagy hozzáadhatnánk a Hőmérséklett, a Páratartalomt és a Légnyomást változókat, hogy az eső feltételeinek fizikai modelljeit felhasználhassuk.
15.2. ábra - Az esernyős világot leíró Bayes-hálóstruktúra és feltételes eloszlások. Az álapotátmenet-modell a P(Esőt|Esőt–1) feltételes valószínűség-eloszlás, az érzékelő modell a P(Esernyőtt|Esőt).
A 15.1. feladat annak megmutatását kéri, hogy az első megoldás – a folyamat rendjének a megnövelése – mindig átfogalmazható az állapotváltozók halmazának megnövelésére, változatlanul hagyva a rendet. Vegyük észre, hogy állapotváltozók hozzáadása javíthatja a rendszer előrejelző erejét, de megnöveli a predikciós követelményeket is: ekkor már az új változókat is jósolni kell. Így a változóknak egy „önmagában elégséges” halmazát keressük, ami valójában azt jelenti, hogy meg kell értenünk a modellezett folyamat „fizikáját”. A folyamat pontos modellezése iránti követelmény nyilvánvalóan mérsékeltebb, ha új érzékelőket vehetünk fel (például a hőmérséklet és a nyomás mérésére), amelyek közvetlenül az új állapotváltozókról szolgáltatnak információt.
Gondoljuk meg például egy X–Y síkon véletlenszerűen sétáló robot követésének a problémáját. Egy javaslat az állapotváltozók egy elégséges halmazára ekkor a pozíció és a sebesség lehet: Newton törvényeit felhasználva kiszámolható az új pozíció, és a sebesség megjósolhatatlanul változik. Ha azonban a robot akkumulátorról üzemel, akkor az elem lemerülésének tipikusan van egy szisztematikus hatása a sebesség megváltozására. Mivel ez viszont függ attól, hogy mennyi energia használódott el az összes korábbi manőverben, a Markov-tulajdonság sérül. A Markov-tulajdonságot helyreállíthatjuk egy Akkumulátort feltöltöttségi szintnek mint az Xt-t alkotó állapotváltozók egyikének a felvételével. Ez segít a robot mozgásának a jóslásában, de ugyanakkor megköveteli az Akkumulátort jóslását az Akkumulátort–1-ből és a sebességből. Bizonyos esetekben ez megbízhatóan megtehető; a pontosság azonban javulna egy, az akkumulátor feltöltöttségét mérő új érzékelő felvételével.
